Towards Automated Model Design on Recommender Systems

The increasing popularity of deep learning models has created new opportunities for developing AI-based recommender systems. Designing recommender systems using deep neural networks requires careful architecture design, and further optimization demands extensive co-design efforts on jointly optimizing model architecture and hardware. Design automation, such as Automated Machine Learning (AutoML), is necessary to fully exploit the potential of recommender model design, including model choices and model-hardware co-design strategies. We introduce a novel paradigm that utilizes weight sharing to explore abundant solution spaces. Our paradigm creates a large supernet to search for optimal architectures and co-design strategies to address the challenges of data multi-modality and heterogeneity in the recommendation domain. From a model perspective, the supernet includes a variety of operators, dense connectivity, and dimension search options. From a co-design perspective, it encompasses versatile Processing-In-Memory (PIM) configurations to produce hardware-efficient models. Our solution space's scale, heterogeneity, and complexity pose several challenges, which we address by proposing various techniques for training and evaluating the supernet. Our crafted models show promising results on three Click-Through Rates (CTR) prediction benchmarks, outperforming both manually designed and AutoML-crafted models with state-of-the-art performance when focusing solely on architecture search. From a co-design perspective, we achieve 2x FLOPs efficiency, 1.8x energy efficiency, and 1.5x performance improvements in recommender models.

Rankitect: Ranking Architecture Search Battling World-class Engineers at Meta Scale

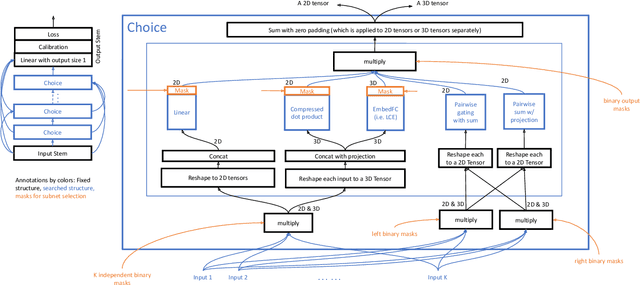
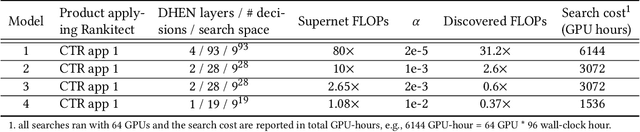
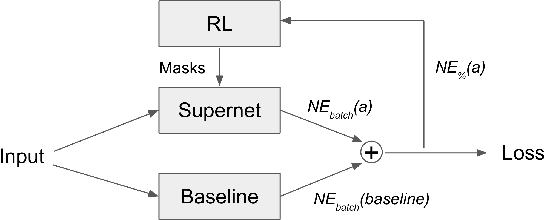
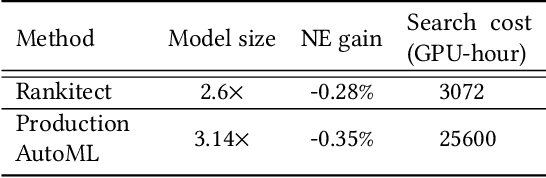
Neural Architecture Search (NAS) has demonstrated its efficacy in computer vision and potential for ranking systems. However, prior work focused on academic problems, which are evaluated at small scale under well-controlled fixed baselines. In industry system, such as ranking system in Meta, it is unclear whether NAS algorithms from the literature can outperform production baselines because of: (1) scale - Meta ranking systems serve billions of users, (2) strong baselines - the baselines are production models optimized by hundreds to thousands of world-class engineers for years since the rise of deep learning, (3) dynamic baselines - engineers may have established new and stronger baselines during NAS search, and (4) efficiency - the search pipeline must yield results quickly in alignment with the productionization life cycle. In this paper, we present Rankitect, a NAS software framework for ranking systems at Meta. Rankitect seeks to build brand new architectures by composing low level building blocks from scratch. Rankitect implements and improves state-of-the-art (SOTA) NAS methods for comprehensive and fair comparison under the same search space, including sampling-based NAS, one-shot NAS, and Differentiable NAS (DNAS). We evaluate Rankitect by comparing to multiple production ranking models at Meta. We find that Rankitect can discover new models from scratch achieving competitive tradeoff between Normalized Entropy loss and FLOPs. When utilizing search space designed by engineers, Rankitect can generate better models than engineers, achieving positive offline evaluation and online A/B test at Meta scale.

NASRec: Weight Sharing Neural Architecture Search for Recommender Systems

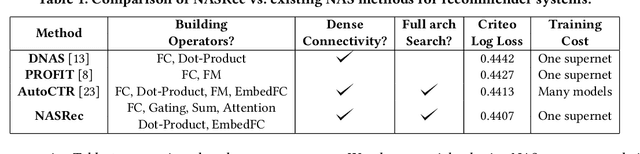
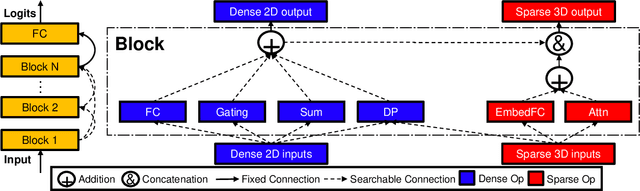
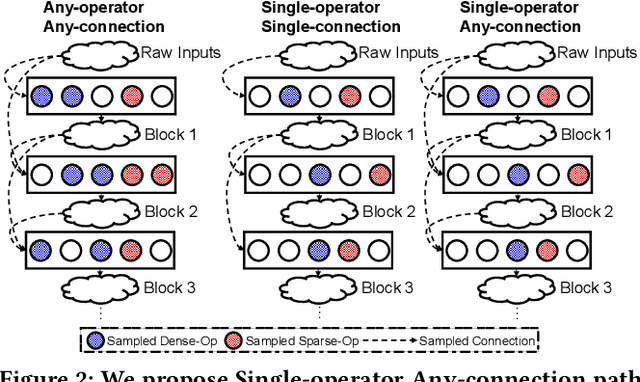
The rise of deep neural networks provides an important driver in optimizing recommender systems. However, the success of recommender systems lies in delicate architecture fabrication, and thus calls for Neural Architecture Search (NAS) to further improve its modeling. We propose NASRec, a paradigm that trains a single supernet and efficiently produces abundant models/sub-architectures by weight sharing. To overcome the data multi-modality and architecture heterogeneity challenges in recommendation domain, NASRec establishes a large supernet (i.e., search space) to search the full architectures, with the supernet incorporating versatile operator choices and dense connectivity minimizing human prior for flexibility. The scale and heterogeneity in NASRec impose challenges in search, such as training inefficiency, operator-imbalance, and degraded rank correlation. We tackle these challenges by proposing single-operator any-connection sampling, operator-balancing interaction modules, and post-training fine-tuning. Our results on three Click-Through Rates (CTR) prediction benchmarks show that NASRec can outperform both manually designed models and existing NAS methods, achieving state-of-the-art performance.

Towards Automated Neural Interaction Discovery for Click-Through Rate Prediction

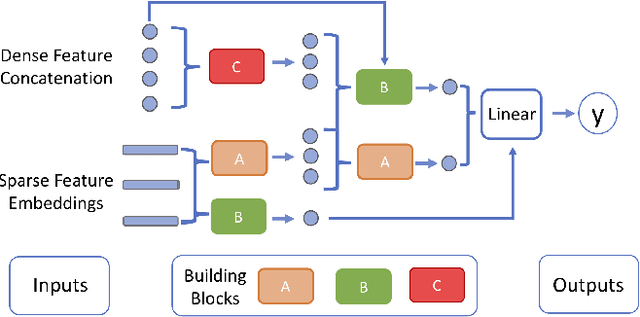
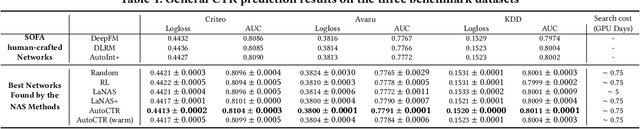
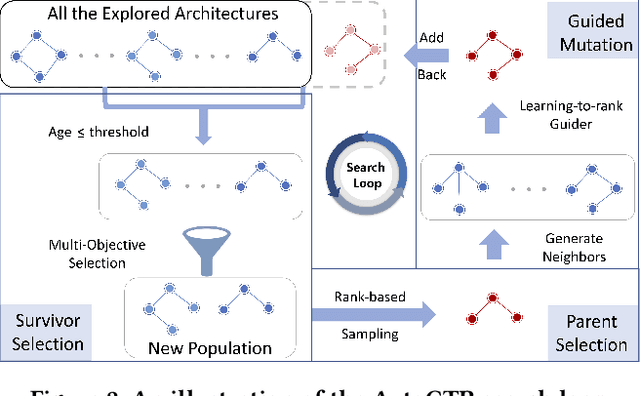
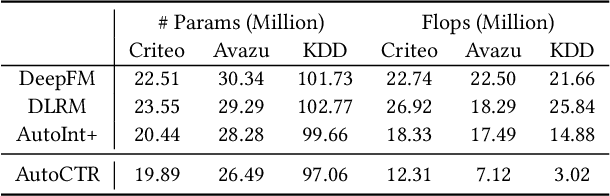
Click-Through Rate (CTR) prediction is one of the most important machine learning tasks in recommender systems, driving personalized experience for billions of consumers. Neural architecture search (NAS), as an emerging field, has demonstrated its capabilities in discovering powerful neural network architectures, which motivates us to explore its potential for CTR predictions. Due to 1) diverse unstructured feature interactions, 2) heterogeneous feature space, and 3) high data volume and intrinsic data randomness, it is challenging to construct, search, and compare different architectures effectively for recommendation models. To address these challenges, we propose an automated interaction architecture discovering framework for CTR prediction named AutoCTR. Via modularizing simple yet representative interactions as virtual building blocks and wiring them into a space of direct acyclic graphs, AutoCTR performs evolutionary architecture exploration with learning-to-rank guidance at the architecture level and achieves acceleration using low-fidelity model. Empirical analysis demonstrates the effectiveness of AutoCTR on different datasets comparing to human-crafted architectures. The discovered architecture also enjoys generalizability and transferability among different datasets.

Feature Interaction Interpretability: A Case for Explaining Ad-Recommendation Systems via Neural Interaction Detection

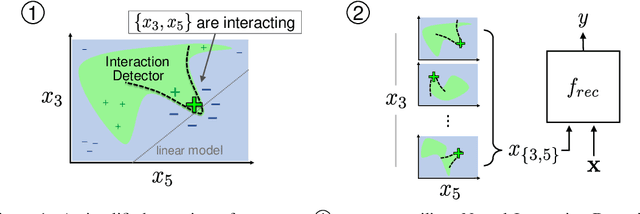
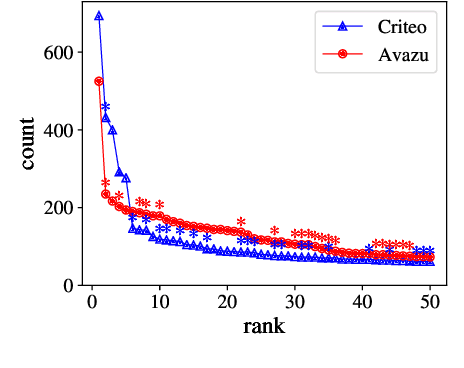
Recommendation is a prevalent application of machine learning that affects many users; therefore, it is important for recommender models to be accurate and interpretable. In this work, we propose a method to both interpret and augment the predictions of black-box recommender systems. In particular, we propose to interpret feature interactions from a source recommender model and explicitly encode these interactions in a target recommender model, where both source and target models are black-boxes. By not assuming the structure of the recommender system, our approach can be used in general settings. In our experiments, we focus on a prominent use of machine learning recommendation: ad-click prediction. We found that our interaction interpretations are both informative and predictive, e.g., significantly outperforming existing recommender models. What's more, the same approach to interpret interactions can provide new insights into domains even beyond recommendation, such as text and image classification.

Detecting Statistical Interactions from Neural Network Weights

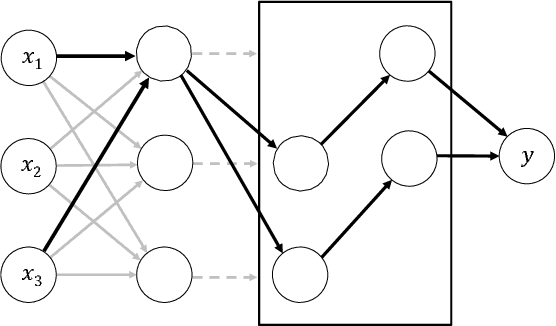
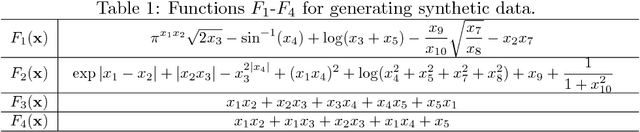
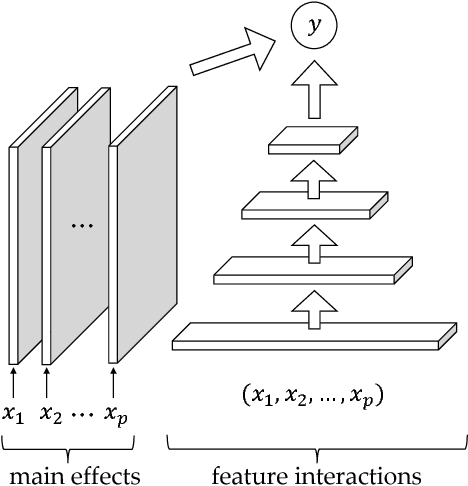
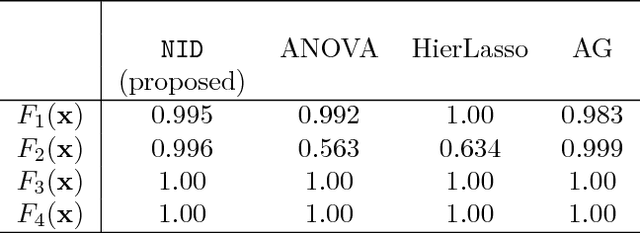
Interpreting neural networks is a crucial and challenging task in machine learning. In this paper, we develop a novel framework for detecting statistical interactions captured by a feedforward multilayer neural network by directly interpreting its learned weights. Depending on the desired interactions, our method can achieve significantly better or similar interaction detection performance compared to the state-of-the-art without searching an exponential solution space of possible interactions. We obtain this accuracy and efficiency by observing that interactions between input features are created by the non-additive effect of nonlinear activation functions, and that interacting paths are encoded in weight matrices. We demonstrate the performance of our method and the importance of discovered interactions via experimental results on both synthetic datasets and real-world application datasets.

On Bochner's and Polya's Characterizations of Positive-Definite Kernels and the Respective Random Feature Maps

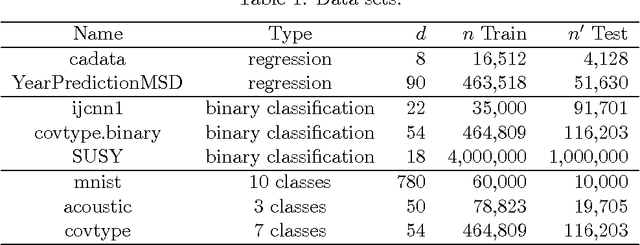
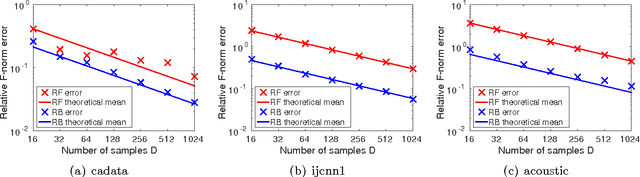
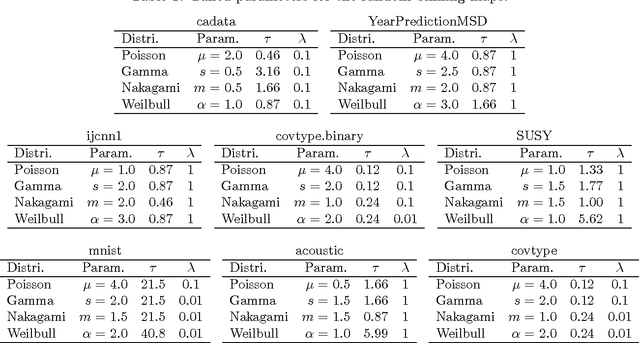
Positive-definite kernel functions are fundamental elements of kernel methods and Gaussian processes. A well-known construction of such functions comes from Bochner's characterization, which connects a positive-definite function with a probability distribution. Another construction, which appears to have attracted less attention, is Polya's criterion that characterizes a subset of these functions. In this paper, we study the latter characterization and derive a number of novel kernels little known previously. In the context of large-scale kernel machines, Rahimi and Recht (2007) proposed a random feature map (random Fourier) that approximates a kernel function, through independent sampling of the probability distribution in Bochner's characterization. The authors also suggested another feature map (random binning), which, although not explicitly stated, comes from Polya's characterization. We show that with the same number of random samples, the random binning map results in an Euclidean inner product closer to the kernel than does the random Fourier map. The superiority of the random binning map is confirmed empirically through regressions and classifications in the reproducing kernel Hilbert space.

Model Selection for Topic Models via Spectral Decomposition

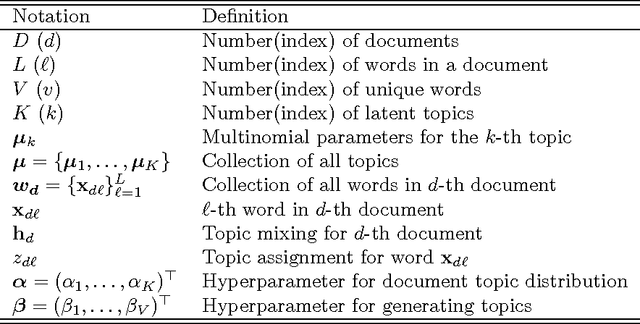
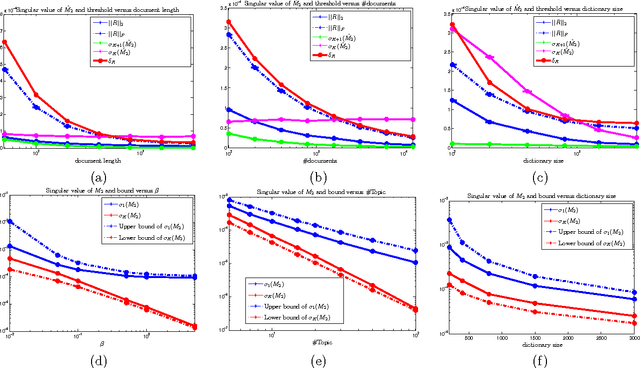
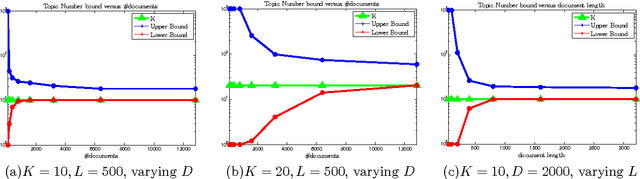
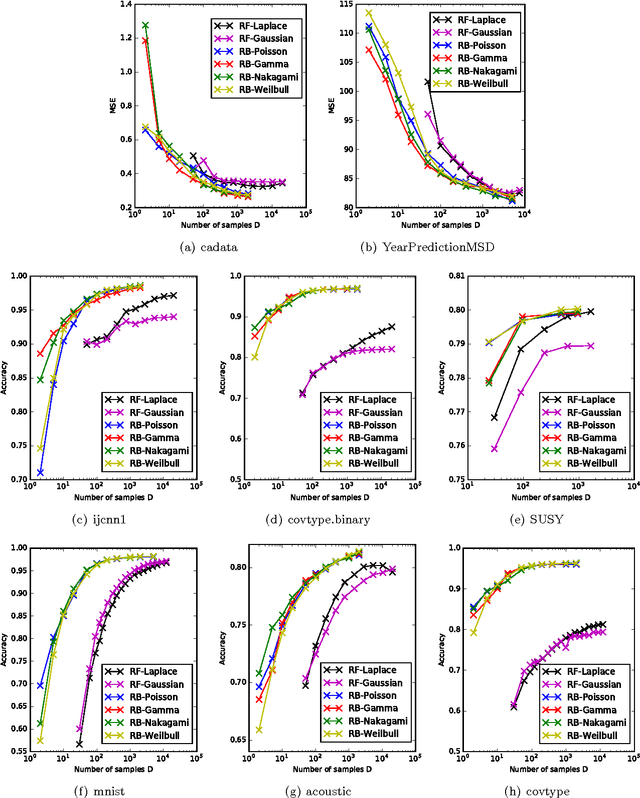
Topic models have achieved significant successes in analyzing large-scale text corpus. In practical applications, we are always confronted with the challenge of model selection, i.e., how to appropriately set the number of topics. Following recent advances in topic model inference via tensor decomposition, we make a first attempt to provide theoretical analysis on model selection in latent Dirichlet allocation. Under mild conditions, we derive the upper bound and lower bound on the number of topics given a text collection of finite size. Experimental results demonstrate that our bounds are accurate and tight. Furthermore, using Gaussian mixture model as an example, we show that our methodology can be easily generalized to model selection analysis for other latent models.

Spectral Sparsification of Random-Walk Matrix Polynomials

We consider a fundamental algorithmic question in spectral graph theory: Compute a spectral sparsifier of random-walk matrix-polynomial $$L_\alpha(G)=D-\sum_{r=1}^d\alpha_rD(D^{-1}A)^r$$ where $A$ is the adjacency matrix of a weighted, undirected graph, $D$ is the diagonal matrix of weighted degrees, and $\alpha=(\alpha_1...\alpha_d)$ are nonnegative coefficients with $\sum_{r=1}^d\alpha_r=1$. Recall that $D^{-1}A$ is the transition matrix of random walks on the graph. The sparsification of $L_\alpha(G)$ appears to be algorithmically challenging as the matrix power $(D^{-1}A)^r$ is defined by all paths of length $r$, whose precise calculation would be prohibitively expensive. In this paper, we develop the first nearly linear time algorithm for this sparsification problem: For any $G$ with $n$ vertices and $m$ edges, $d$ coefficients $\alpha$, and $\epsilon > 0$, our algorithm runs in time $O(d^2m\log^2n/\epsilon^{2})$ to construct a Laplacian matrix $\tilde{L}=D-\tilde{A}$ with $O(n\log n/\epsilon^{2})$ non-zeros such that $\tilde{L}\approx_{\epsilon}L_\alpha(G)$. Matrix polynomials arise in mathematical analysis of matrix functions as well as numerical solutions of matrix equations. Our work is particularly motivated by the algorithmic problems for speeding up the classic Newton's method in applications such as computing the inverse square-root of the precision matrix of a Gaussian random field, as well as computing the $q$th-root transition (for $q\geq1$) in a time-reversible Markov model. The key algorithmic step for both applications is the construction of a spectral sparsifier of a constant degree random-walk matrix-polynomials introduced by Newton's method. Our algorithm can also be used to build efficient data structures for effective resistances for multi-step time-reversible Markov models, and we anticipate that it could be useful for other tasks in network analysis.

Scalable Parallel Factorizations of SDD Matrices and Efficient Sampling for Gaussian Graphical Models

Motivated by a sampling problem basic to computational statistical inference, we develop a nearly optimal algorithm for a fundamental problem in spectral graph theory and numerical analysis. Given an $n\times n$ SDDM matrix ${\bf \mathbf{M}}$, and a constant $-1 \leq p \leq 1$, our algorithm gives efficient access to a sparse $n\times n$ linear operator $\tilde{\mathbf{C}}$ such that $${\mathbf{M}}^{p} \approx \tilde{\mathbf{C}} \tilde{\mathbf{C}}^\top.$$ The solution is based on factoring ${\bf \mathbf{M}}$ into a product of simple and sparse matrices using squaring and spectral sparsification. For ${\mathbf{M}}$ with $m$ non-zero entries, our algorithm takes work nearly-linear in $m$, and polylogarithmic depth on a parallel machine with $m$ processors. This gives the first sampling algorithm that only requires nearly linear work and $n$ i.i.d. random univariate Gaussian samples to generate i.i.d. random samples for $n$-dimensional Gaussian random fields with SDDM precision matrices. For sampling this natural subclass of Gaussian random fields, it is optimal in the randomness and nearly optimal in the work and parallel complexity. In addition, our sampling algorithm can be directly extended to Gaussian random fields with SDD precision matrices.