Model Selection for Topic Models via Spectral Decomposition
Paper and Code
Feb 17, 2015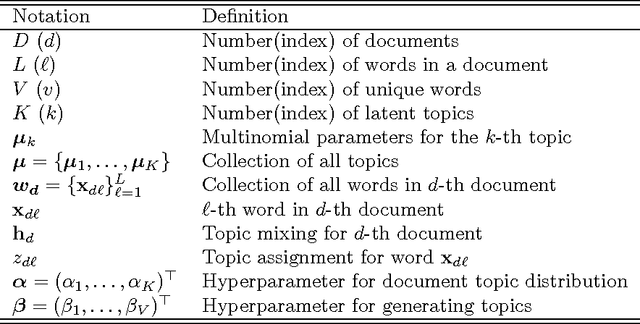
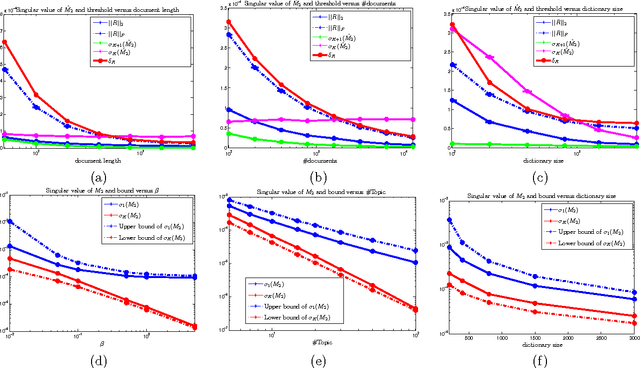
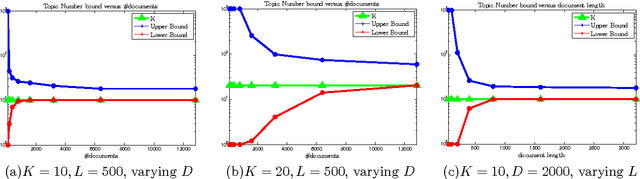
Topic models have achieved significant successes in analyzing large-scale text corpus. In practical applications, we are always confronted with the challenge of model selection, i.e., how to appropriately set the number of topics. Following recent advances in topic model inference via tensor decomposition, we make a first attempt to provide theoretical analysis on model selection in latent Dirichlet allocation. Under mild conditions, we derive the upper bound and lower bound on the number of topics given a text collection of finite size. Experimental results demonstrate that our bounds are accurate and tight. Furthermore, using Gaussian mixture model as an example, we show that our methodology can be easily generalized to model selection analysis for other latent models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge