SVIA: A Street View Image Anonymization Framework for Self-Driving Applications

In recent years, there has been an increasing interest in image anonymization, particularly focusing on the de-identification of faces and individuals. However, for self-driving applications, merely de-identifying faces and individuals might not provide sufficient privacy protection since street views like vehicles and buildings can still disclose locations, trajectories, and other sensitive information. Therefore, it remains crucial to extend anonymization techniques to street view images to fully preserve the privacy of users, pedestrians, and vehicles. In this paper, we propose a Street View Image Anonymization (SVIA) framework for self-driving applications. The SVIA framework consists of three integral components: a semantic segmenter to segment an input image into functional regions, an inpainter to generate alternatives to privacy-sensitive regions, and a harmonizer to seamlessly stitch modified regions to guarantee visual coherence. Compared to existing methods, SVIA achieves a much better trade-off between image generation quality and privacy protection, as evidenced by experimental results for five common metrics on two widely used public datasets.

Enhanced Multimodal RAG-LLM for Accurate Visual Question Answering

Multimodal large language models (MLLMs), such as GPT-4o, Gemini, LLaVA, and Flamingo, have made significant progress in integrating visual and textual modalities, excelling in tasks like visual question answering (VQA), image captioning, and content retrieval. They can generate coherent and contextually relevant descriptions of images. However, they still face challenges in accurately identifying and counting objects and determining their spatial locations, particularly in complex scenes with overlapping or small objects. To address these limitations, we propose a novel framework based on multimodal retrieval-augmented generation (RAG), which introduces structured scene graphs to enhance object recognition, relationship identification, and spatial understanding within images. Our framework improves the MLLM's capacity to handle tasks requiring precise visual descriptions, especially in scenarios with challenging perspectives, such as aerial views or scenes with dense object arrangements. Finally, we conduct extensive experiments on the VG-150 dataset that focuses on first-person visual understanding and the AUG dataset that involves aerial imagery. The results show that our approach consistently outperforms existing MLLMs in VQA tasks, which stands out in recognizing, localizing, and quantifying objects in different spatial contexts and provides more accurate visual descriptions.

PediaBench: A Comprehensive Chinese Pediatric Dataset for Benchmarking Large Language Models

The emergence of Large Language Models (LLMs) in the medical domain has stressed a compelling need for standard datasets to evaluate their question-answering (QA) performance. Although there have been several benchmark datasets for medical QA, they either cover common knowledge across different departments or are specific to another department rather than pediatrics. Moreover, some of them are limited to objective questions and do not measure the generation capacity of LLMs. Therefore, they cannot comprehensively assess the QA ability of LLMs in pediatrics. To fill this gap, we construct PediaBench, the first Chinese pediatric dataset for LLM evaluation. Specifically, it contains 4,565 objective questions and 1,632 subjective questions spanning 12 pediatric disease groups. It adopts an integrated scoring criterion based on different difficulty levels to thoroughly assess the proficiency of an LLM in instruction following, knowledge understanding, clinical case analysis, etc. Finally, we validate the effectiveness of PediaBench with extensive experiments on 20 open-source and commercial LLMs. Through an in-depth analysis of experimental results, we offer insights into the ability of LLMs to answer pediatric questions in the Chinese context, highlighting their limitations for further improvements. Our code and data are published at https://github.com/ACMISLab/PediaBench.

FedMCP: Parameter-Efficient Federated Learning with Model-Contrastive Personalization

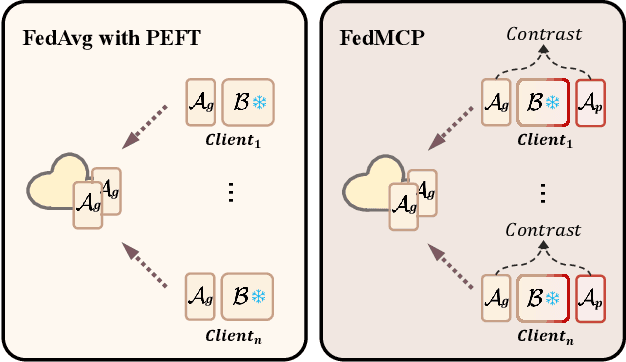
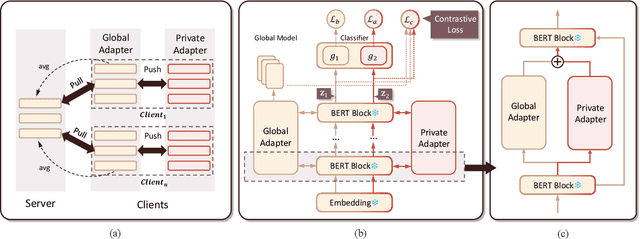
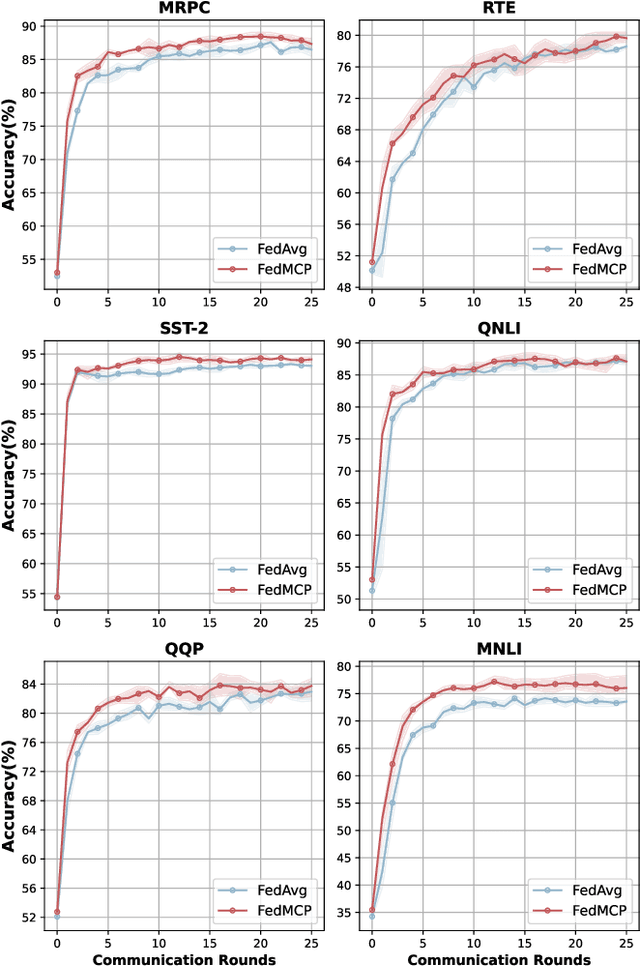
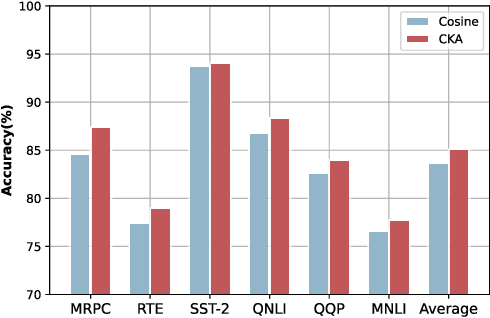
With increasing concerns and regulations on data privacy, fine-tuning pretrained language models (PLMs) in federated learning (FL) has become a common paradigm for NLP tasks. Despite being extensively studied, the existing methods for this problem still face two primary challenges. First, the huge number of parameters in large-scale PLMs leads to excessive communication and computational overhead. Second, the heterogeneity of data and tasks across clients poses a significant obstacle to achieving the desired fine-tuning performance. To address the above problems, we propose FedMCP, a novel parameter-efficient fine-tuning method with model-contrastive personalization for FL. Specifically, FedMCP adds two lightweight adapter modules, i.e., the global adapter and the private adapter, to the frozen PLMs within clients. In a communication round, each client sends only the global adapter to the server for federated aggregation. Furthermore, FedMCP introduces a model-contrastive regularization term between the two adapters. This, on the one hand, encourages the global adapter to assimilate universal knowledge and, on the other hand, the private adapter to capture client-specific knowledge. By leveraging both adapters, FedMCP can effectively provide fine-tuned personalized models tailored to individual clients. Extensive experiments on highly heterogeneous cross-task, cross-silo datasets show that FedMCP achieves substantial performance improvements over state-of-the-art FL fine-tuning approaches for PLMs.

DPSW-Sketch: A Differentially Private Sketch Framework for Frequency Estimation over Sliding Windows (Technical Report)

The sliding window model of computation captures scenarios in which data are continually arriving in the form of a stream, and only the most recent $w$ items are used for analysis. In this setting, an algorithm needs to accurately track some desired statistics over the sliding window using a small space. When data streams contain sensitive information about individuals, the algorithm is also urgently needed to provide a provable guarantee of privacy. In this paper, we focus on the two fundamental problems of privately (1) estimating the frequency of an arbitrary item and (2) identifying the most frequent items (i.e., \emph{heavy hitters}), in the sliding window model. We propose \textsc{DPSW-Sketch}, a sliding window framework based on the count-min sketch that not only satisfies differential privacy over the stream but also approximates the results for frequency and heavy-hitter queries within bounded errors in sublinear time and space w.r.t.~$w$. Extensive experiments on five real-world and synthetic datasets show that \textsc{DPSW-Sketch} provides significantly better utility-privacy trade-offs than state-of-the-art methods.

Diversity-Aware $k$-Maximum Inner Product Search Revisited

The $k$-Maximum Inner Product Search ($k$MIPS) serves as a foundational component in recommender systems and various data mining tasks. However, while most existing $k$MIPS approaches prioritize the efficient retrieval of highly relevant items for users, they often neglect an equally pivotal facet of search results: \emph{diversity}. To bridge this gap, we revisit and refine the diversity-aware $k$MIPS (D$k$MIPS) problem by incorporating two well-known diversity objectives -- minimizing the average and maximum pairwise item similarities within the results -- into the original relevance objective. This enhancement, inspired by Maximal Marginal Relevance (MMR), offers users a controllable trade-off between relevance and diversity. We introduce \textsc{Greedy} and \textsc{DualGreedy}, two linear scan-based algorithms tailored for D$k$MIPS. They both achieve data-dependent approximations and, when aiming to minimize the average pairwise similarity, \textsc{DualGreedy} attains an approximation ratio of $1/4$ with an additive term for regularization. To further improve query efficiency, we integrate a lightweight Ball-Cone Tree (BC-Tree) index with the two algorithms. Finally, comprehensive experiments on ten real-world data sets demonstrate the efficacy of our proposed methods, showcasing their capability to efficiently deliver diverse and relevant search results to users.

Workload-aware and Learned Z-Indexes

In this paper, we present a learned and workload-aware variant of a Z-index, which jointly optimizes storage layout and search structures. Specifically, we first formulate a cost function to measure the performance of a Z-index on a dataset for a range-query workload. Then, we optimize the Z-index structure by minimizing the cost function through adaptive partitioning and ordering for index construction. Moreover, we design a novel page-skipping mechanism to improve its query performance by reducing access to irrelevant data pages. Our extensive experiments show that our index improves range query time by 40% on average over the baselines, while always performing better or comparably to state-of-the-art spatial indexes. Additionally, our index maintains good point query performance while providing favourable construction time and index size tradeoffs.

Spectral Normalized-Cut Graph Partitioning with Fairness Constraints

Normalized-cut graph partitioning aims to divide the set of nodes in a graph into $k$ disjoint clusters to minimize the fraction of the total edges between any cluster and all other clusters. In this paper, we consider a fair variant of the partitioning problem wherein nodes are characterized by a categorical sensitive attribute (e.g., gender or race) indicating membership to different demographic groups. Our goal is to ensure that each group is approximately proportionally represented in each cluster while minimizing the normalized cut value. To resolve this problem, we propose a two-phase spectral algorithm called FNM. In the first phase, we add an augmented Lagrangian term based on our fairness criteria to the objective function for obtaining a fairer spectral node embedding. Then, in the second phase, we design a rounding scheme to produce $k$ clusters from the fair embedding that effectively trades off fairness and partition quality. Through comprehensive experiments on nine benchmark datasets, we demonstrate the superior performance of FNM compared with three baseline methods.

Max-Min Diversification with Fairness Constraints: Exact and Approximation Algorithms

Diversity maximization aims to select a diverse and representative subset of items from a large dataset. It is a fundamental optimization task that finds applications in data summarization, feature selection, web search, recommender systems, and elsewhere. However, in a setting where data items are associated with different groups according to sensitive attributes like sex or race, it is possible that algorithmic solutions for this task, if left unchecked, will under- or over-represent some of the groups. Therefore, we are motivated to address the problem of \emph{max-min diversification with fairness constraints}, aiming to select $k$ items to maximize the minimum distance between any pair of selected items while ensuring that the number of items selected from each group falls within predefined lower and upper bounds. In this work, we propose an exact algorithm based on integer linear programming that is suitable for small datasets as well as a $\frac{1-\varepsilon}{5}$-approximation algorithm for any $\varepsilon \in (0, 1)$ that scales to large datasets. Extensive experiments on real-world datasets demonstrate the superior performance of our proposed algorithms over existing ones.

SAH: Shifting-aware Asymmetric Hashing for Reverse $k$-Maximum Inner Product Search

This paper investigates a new yet challenging problem called Reverse $k$-Maximum Inner Product Search (R$k$MIPS). Given a query (item) vector, a set of item vectors, and a set of user vectors, the problem of R$k$MIPS aims to find a set of user vectors whose inner products with the query vector are one of the $k$ largest among the query and item vectors. We propose the first subquadratic-time algorithm, i.e., Shifting-aware Asymmetric Hashing (SAH), to tackle the R$k$MIPS problem. To speed up the Maximum Inner Product Search (MIPS) on item vectors, we design a shifting-invariant asymmetric transformation and develop a novel sublinear-time Shifting-Aware Asymmetric Locality Sensitive Hashing (SA-ALSH) scheme. Furthermore, we devise a new blocking strategy based on the Cone-Tree to effectively prune user vectors (in a batch). We prove that SAH achieves a theoretical guarantee for solving the RMIPS problem. Experimental results on five real-world datasets show that SAH runs 4$\sim$8$\times$ faster than the state-of-the-art methods for R$k$MIPS while achieving F1-scores of over 90\%. The code is available at \url{https://github.com/HuangQiang/SAH}.