Many Needles in a Haystack: Active Hit Discovery for Perturbation Experiments

High-throughput gene perturbation experiments can test several genetic interventions in parallel, yet experimental budgets remain limited. A central goal is hit discovery: identifying as many perturbations as possible whose phenotypic effect exceeds a predefined threshold. Pure exploration strategies are statistically inefficient, wasting budget on low-value regions. Bayesian optimization methods offer a principled alternative but target a single global optimum, over-exploiting dominant modes while neglecting other high-value regions. We formalize hit discovery as a sequential experimental design problem and propose Probability-of-Hit, an acquisition function that directly targets threshold exceedance by ranking candidates according to their posterior probability of being a hit. We prove asymptotic optimality of this approach and demonstrate strong empirical performance on both synthetic benchmarks and real biological immunology datasets, including up to 6.4% improvement over baselines on the Schmidt IL-2 dataset.

Disparity, Inequality, and Accuracy Tradeoffs in Graph Neural Networks for Node Classification

Graph neural networks (GNNs) are increasingly used in critical human applications for predicting node labels in attributed graphs. Their ability to aggregate features from nodes' neighbors for accurate classification also has the capacity to exacerbate existing biases in data or to introduce new ones towards members from protected demographic groups. Thus, it is imperative to quantify how GNNs may be biased and to what extent their harmful effects may be mitigated. To this end, we propose two new GNN-agnostic interventions namely, (i) PFR-AX which decreases the separability between nodes in protected and non-protected groups, and (ii) PostProcess which updates model predictions based on a blackbox policy to minimize differences between error rates across demographic groups. Through a large set of experiments on four datasets, we frame the efficacies of our approaches (and three variants) in terms of their algorithmic fairness-accuracy tradeoff and benchmark our results against three strong baseline interventions on three state-of-the-art GNN models. Our results show that no single intervention offers a universally optimal tradeoff, but PFR-AX and PostProcess provide granular control and improve model confidence when correctly predicting positive outcomes for nodes in protected groups.

Spectral Normalized-Cut Graph Partitioning with Fairness Constraints

Normalized-cut graph partitioning aims to divide the set of nodes in a graph into $k$ disjoint clusters to minimize the fraction of the total edges between any cluster and all other clusters. In this paper, we consider a fair variant of the partitioning problem wherein nodes are characterized by a categorical sensitive attribute (e.g., gender or race) indicating membership to different demographic groups. Our goal is to ensure that each group is approximately proportionally represented in each cluster while minimizing the normalized cut value. To resolve this problem, we propose a two-phase spectral algorithm called FNM. In the first phase, we add an augmented Lagrangian term based on our fairness criteria to the objective function for obtaining a fairer spectral node embedding. Then, in the second phase, we design a rounding scheme to produce $k$ clusters from the fair embedding that effectively trades off fairness and partition quality. Through comprehensive experiments on nine benchmark datasets, we demonstrate the superior performance of FNM compared with three baseline methods.

Graph Summarization via Node Grouping: A Spectral Algorithm

Graph summarization via node grouping is a popular method to build concise graph representations by grouping nodes from the original graph into supernodes and encoding edges into superedges such that the loss of adjacency information is minimized. Such summaries have immense applications in large-scale graph analytics due to their small size and high query processing efficiency. In this paper, we reformulate the loss minimization problem for summarization into an equivalent integer maximization problem. By initially allowing relaxed (fractional) solutions for integer maximization, we analytically expose the underlying connections to the spectral properties of the adjacency matrix. Consequently, we design an algorithm called SpecSumm that consists of two phases. In the first phase, motivated by spectral graph theory, we apply k-means clustering on the k largest (in magnitude) eigenvectors of the adjacency matrix to assign nodes to supernodes. In the second phase, we propose a greedy heuristic that updates the initial assignment to further improve summary quality. Finally, via extensive experiments on 11 datasets, we show that SpecSumm efficiently produces high-quality summaries compared to state-of-the-art summarization algorithms and scales to graphs with millions of nodes.

Joint Use of Node Attributes and Proximity for Semi-Supervised Classification on Graphs

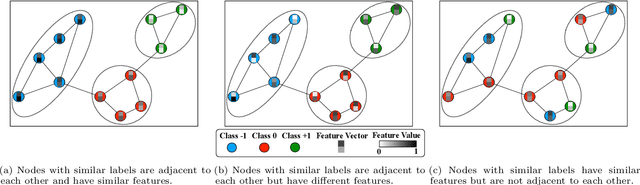
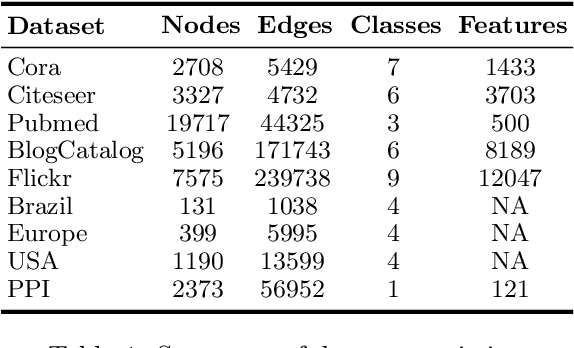
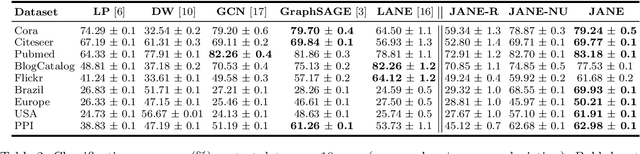
The node classification problem is to infer unknown node labels in a graph given its structure and node attributes along with labels for some of the nodes. Approaches for this task typically assume that adjacent nodes have similar attributes and thus, that a node's label can be predicted from the labels of its neighbors. While such homophily is often observed (e.g., for political affiliation in social networks), the assumption may not hold for arbitrary graph datasets and classification tasks. In fact, nodes that share the same label may be adjacent but differ in their attributes; or may not be adjacent but have similar attributes. We aim to develop a node classification approach that can flexibly adapt to a range of settings wherein labels are correlated with graph structure, or node attributes, or both. To this end, we propose JANE (Jointly using Attributes and Node Embeddings): a novel and principled approach based on a generative probabilistic model that weighs the role of node proximity and attribute similarity in predicting labels. Our experiments on a variety of graph datasets and comparison with standard baselines demonstrate that JANE exhibits a superior combination of versatility and competitive performance.

Iterative Classroom Teaching

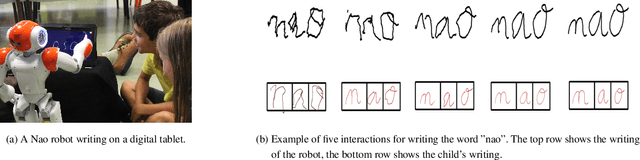
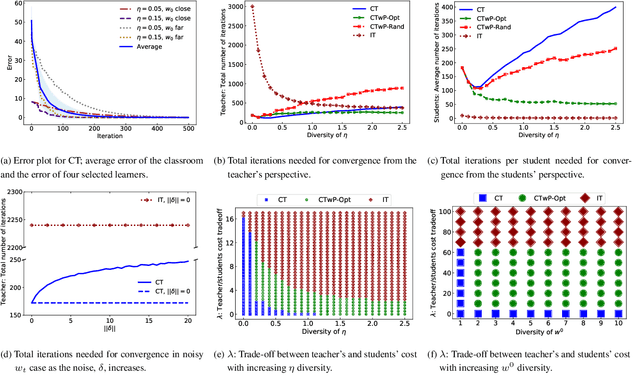
We consider the machine teaching problem in a classroom-like setting wherein the teacher has to deliver the same examples to a diverse group of students. Their diversity stems from differences in their initial internal states as well as their learning rates. We prove that a teacher with full knowledge about the learning dynamics of the students can teach a target concept to the entire classroom using O(min{d,N} log(1/eps)) examples, where d is the ambient dimension of the problem, N is the number of learners, and eps is the accuracy parameter. We show the robustness of our teaching strategy when the teacher has limited knowledge of the learners' internal dynamics as provided by a noisy oracle. Further, we study the trade-off between the learners' workload and the teacher's cost in teaching the target concept. Our experiments validate our theoretical results and suggest that appropriately partitioning the classroom into homogenous groups provides a balance between these two objectives.