Workload-aware and Learned Z-Indexes

In this paper, we present a learned and workload-aware variant of a Z-index, which jointly optimizes storage layout and search structures. Specifically, we first formulate a cost function to measure the performance of a Z-index on a dataset for a range-query workload. Then, we optimize the Z-index structure by minimizing the cost function through adaptive partitioning and ordering for index construction. Moreover, we design a novel page-skipping mechanism to improve its query performance by reducing access to irrelevant data pages. Our extensive experiments show that our index improves range query time by 40% on average over the baselines, while always performing better or comparably to state-of-the-art spatial indexes. Additionally, our index maintains good point query performance while providing favourable construction time and index size tradeoffs.

Cost-Effective Retraining of Machine Learning Models

It is important to retrain a machine learning (ML) model in order to maintain its performance as the data changes over time. However, this can be costly as it usually requires processing the entire dataset again. This creates a trade-off between retraining too frequently, which leads to unnecessary computing costs, and not retraining often enough, which results in stale and inaccurate ML models. To address this challenge, we propose ML systems that make automated and cost-effective decisions about when to retrain an ML model. We aim to optimize the trade-off by considering the costs associated with each decision. Our research focuses on determining whether to retrain or keep an existing ML model based on various factors, including the data, the model, and the predictive queries answered by the model. Our main contribution is a Cost-Aware Retraining Algorithm called Cara, which optimizes the trade-off over streams of data and queries. To evaluate the performance of Cara, we analyzed synthetic datasets and demonstrated that Cara can adapt to different data drifts and retraining costs while performing similarly to an optimal retrospective algorithm. We also conducted experiments with real-world datasets and showed that Cara achieves better accuracy than drift detection baselines while making fewer retraining decisions, ultimately resulting in lower total costs.

Max-Min Diversification with Fairness Constraints: Exact and Approximation Algorithms

Diversity maximization aims to select a diverse and representative subset of items from a large dataset. It is a fundamental optimization task that finds applications in data summarization, feature selection, web search, recommender systems, and elsewhere. However, in a setting where data items are associated with different groups according to sensitive attributes like sex or race, it is possible that algorithmic solutions for this task, if left unchecked, will under- or over-represent some of the groups. Therefore, we are motivated to address the problem of \emph{max-min diversification with fairness constraints}, aiming to select $k$ items to maximize the minimum distance between any pair of selected items while ensuring that the number of items selected from each group falls within predefined lower and upper bounds. In this work, we propose an exact algorithm based on integer linear programming that is suitable for small datasets as well as a $\frac{1-\varepsilon}{5}$-approximation algorithm for any $\varepsilon \in (0, 1)$ that scales to large datasets. Extensive experiments on real-world datasets demonstrate the superior performance of our proposed algorithms over existing ones.

Graph Summarization via Node Grouping: A Spectral Algorithm

Graph summarization via node grouping is a popular method to build concise graph representations by grouping nodes from the original graph into supernodes and encoding edges into superedges such that the loss of adjacency information is minimized. Such summaries have immense applications in large-scale graph analytics due to their small size and high query processing efficiency. In this paper, we reformulate the loss minimization problem for summarization into an equivalent integer maximization problem. By initially allowing relaxed (fractional) solutions for integer maximization, we analytically expose the underlying connections to the spectral properties of the adjacency matrix. Consequently, we design an algorithm called SpecSumm that consists of two phases. In the first phase, motivated by spectral graph theory, we apply k-means clustering on the k largest (in magnitude) eigenvectors of the adjacency matrix to assign nodes to supernodes. In the second phase, we propose a greedy heuristic that updates the initial assignment to further improve summary quality. Finally, via extensive experiments on 11 datasets, we show that SpecSumm efficiently produces high-quality summaries compared to state-of-the-art summarization algorithms and scales to graphs with millions of nodes.

Streaming Algorithms for Diversity Maximization with Fairness Constraints

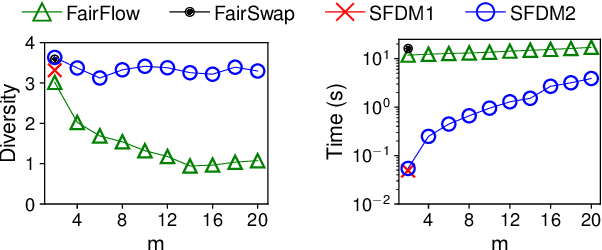
Diversity maximization is a fundamental problem with wide applications in data summarization, web search, and recommender systems. Given a set $X$ of $n$ elements, it asks to select a subset $S$ of $k \ll n$ elements with maximum \emph{diversity}, as quantified by the dissimilarities among the elements in $S$. In this paper, we focus on the diversity maximization problem with fairness constraints in the streaming setting. Specifically, we consider the max-min diversity objective, which selects a subset $S$ that maximizes the minimum distance (dissimilarity) between any pair of distinct elements within it. Assuming that the set $X$ is partitioned into $m$ disjoint groups by some sensitive attribute, e.g., sex or race, ensuring \emph{fairness} requires that the selected subset $S$ contains $k_i$ elements from each group $i \in [1,m]$. A streaming algorithm should process $X$ sequentially in one pass and return a subset with maximum \emph{diversity} while guaranteeing the fairness constraint. Although diversity maximization has been extensively studied, the only known algorithms that can work with the max-min diversity objective and fairness constraints are very inefficient for data streams. Since diversity maximization is NP-hard in general, we propose two approximation algorithms for fair diversity maximization in data streams, the first of which is $\frac{1-\varepsilon}{4}$-approximate and specific for $m=2$, where $\varepsilon \in (0,1)$, and the second of which achieves a $\frac{1-\varepsilon}{3m+2}$-approximation for an arbitrary $m$. Experimental results on real-world and synthetic datasets show that both algorithms provide solutions of comparable quality to the state-of-the-art algorithms while running several orders of magnitude faster in the streaming setting.

Rewiring What-to-Watch-Next Recommendations to Reduce Radicalization Pathways

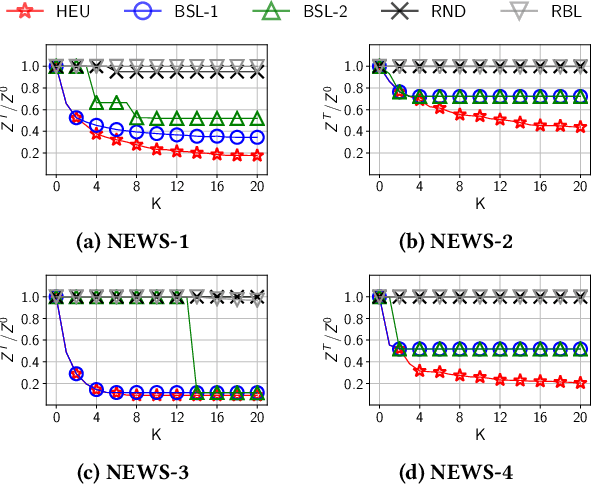
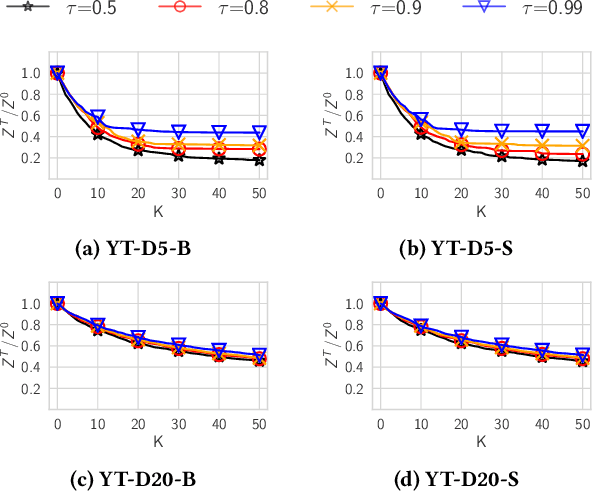
Recommender systems typically suggest to users content similar to what they consumed in the past. If a user happens to be exposed to strongly polarized content, she might subsequently receive recommendations which may steer her towards more and more radicalized content, eventually being trapped in what we call a "radicalization pathway". In this paper, we study the problem of mitigating radicalization pathways using a graph-based approach. Specifically, we model the set of recommendations of a "what-to-watch-next" recommender as a d-regular directed graph where nodes correspond to content items, links to recommendations, and paths to possible user sessions. We measure the "segregation" score of a node representing radicalized content as the expected length of a random walk from that node to any node representing non-radicalized content. High segregation scores are associated to larger chances to get users trapped in radicalization pathways. Hence, we define the problem of reducing the prevalence of radicalization pathways by selecting a small number of edges to "rewire", so to minimize the maximum of segregation scores among all radicalized nodes, while maintaining the relevance of the recommendations. We prove that the problem of finding the optimal set of recommendations to rewire is NP-hard and NP-hard to approximate within any factor. Therefore, we turn our attention to heuristics, and propose an efficient yet effective greedy algorithm based on the absorbing random walk theory. Our experiments on real-world datasets in the context of video and news recommendations confirm the effectiveness of our proposal.

Certifiable Machine Unlearning for Linear Models

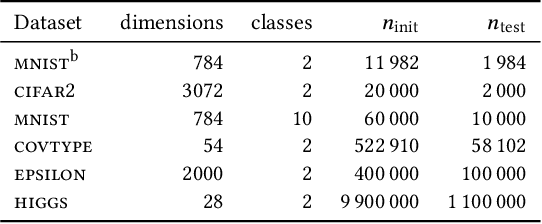
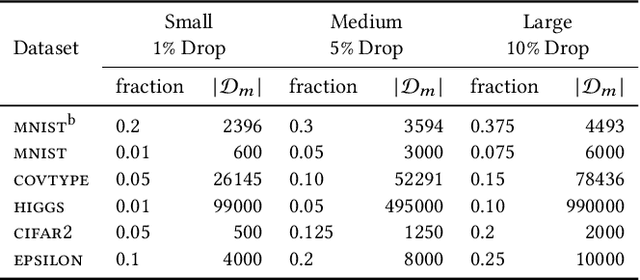
Machine unlearning is the task of updating machine learning (ML) models after a subset of the training data they were trained on is deleted. Methods for the task are desired to combine effectiveness and efficiency, i.e., they should effectively "unlearn" deleted data, but in a way that does not require excessive computation effort (e.g., a full retraining) for a small amount of deletions. Such a combination is typically achieved by tolerating some amount of approximation in the unlearning. In addition, laws and regulations in the spirit of "the right to be forgotten" have given rise to requirements for certifiability, i.e., the ability to demonstrate that the deleted data has indeed been unlearned by the ML model. In this paper, we present an experimental study of the three state-of-the-art approximate unlearning methods for linear models and demonstrate the trade-offs between efficiency, effectiveness and certifiability offered by each method. In implementing the study, we extend some of the existing works and describe a common ML pipeline to compare and evaluate the unlearning methods on six real-world datasets and a variety of settings. We provide insights into the effect of the quantity and distribution of the deleted data on ML models and the performance of each unlearning method in different settings. We also propose a practical online strategy to determine when the accumulated error from approximate unlearning is large enough to warrant a full retrain of the ML model.

Joint Use of Node Attributes and Proximity for Semi-Supervised Classification on Graphs

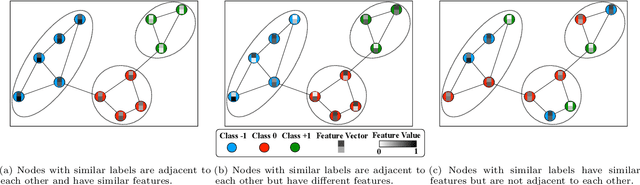
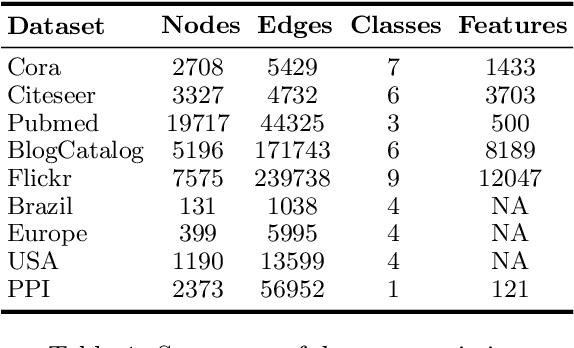
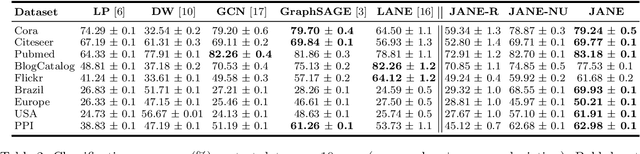
The node classification problem is to infer unknown node labels in a graph given its structure and node attributes along with labels for some of the nodes. Approaches for this task typically assume that adjacent nodes have similar attributes and thus, that a node's label can be predicted from the labels of its neighbors. While such homophily is often observed (e.g., for political affiliation in social networks), the assumption may not hold for arbitrary graph datasets and classification tasks. In fact, nodes that share the same label may be adjacent but differ in their attributes; or may not be adjacent but have similar attributes. We aim to develop a node classification approach that can flexibly adapt to a range of settings wherein labels are correlated with graph structure, or node attributes, or both. To this end, we propose JANE (Jointly using Attributes and Node Embeddings): a novel and principled approach based on a generative probabilistic model that weighs the role of node proximity and attribute similarity in predicting labels. Our experiments on a variety of graph datasets and comparison with standard baselines demonstrate that JANE exhibits a superior combination of versatility and competitive performance.

Streaming Submodular Maximization with Fairness Constraints

We study the problem of extracting a small subset of representative items from a large data stream. Following the convention in many data mining and machine learning applications such as data summarization, recommender systems, and social network analysis, the problem is formulated as maximizing a monotone submodular function subject to a cardinality constraint -- i.e., the size of the selected subset is restricted to be smaller than or equal to an input integer $k$. In this paper, we consider the problem with additional \emph{fairness constraints}, which takes into account the group membership of data items and limits the number of items selected from each group to a given number. We propose efficient algorithms for this fairness-aware variant of the streaming submodular maximization problem. In particular, we first provide a $(\frac{1}{2}-\varepsilon)$-approximation algorithm that requires $O(\frac{1}{\varepsilon} \cdot \log \frac{k}{\varepsilon})$ passes over the stream for any constant $ \varepsilon>0 $. In addition, we design a single-pass streaming algorithm that has the same $(\frac{1}{2}-\varepsilon)$ approximation ratio when unlimited buffer size and post-processing time is permitted.

Towards Data-Driven Affirmative Action Policies under Uncertainty

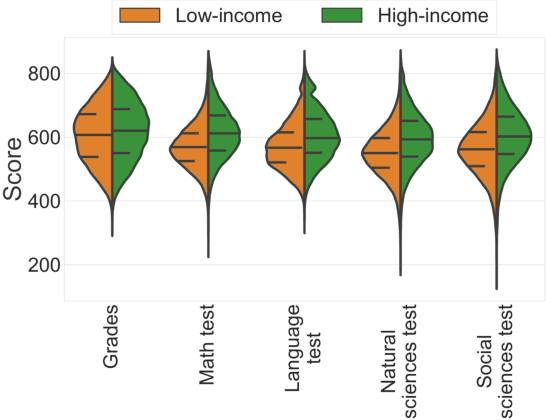
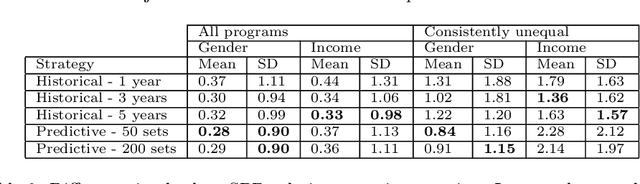
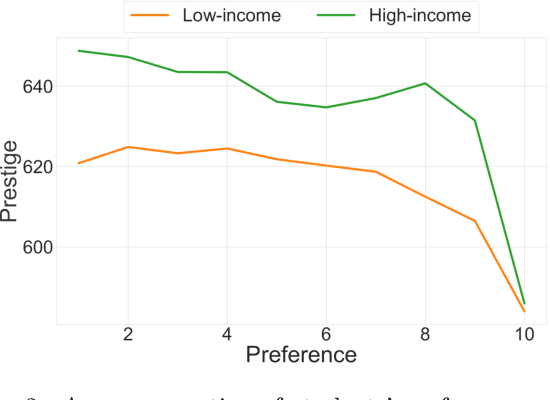
In this paper, we study university admissions under a centralized system that uses grades and standardized test scores to match applicants to university programs. We consider affirmative action policies that seek to increase the number of admitted applicants from underrepresented groups. Since such a policy has to be announced before the start of the application period, there is uncertainty about the score distribution of the students applying to each program. This poses a difficult challenge for policy-makers. We explore the possibility of using a predictive model trained on historical data to help optimize the parameters of such policies.