Beyond the LUMIR challenge: The pathway to foundational registration models

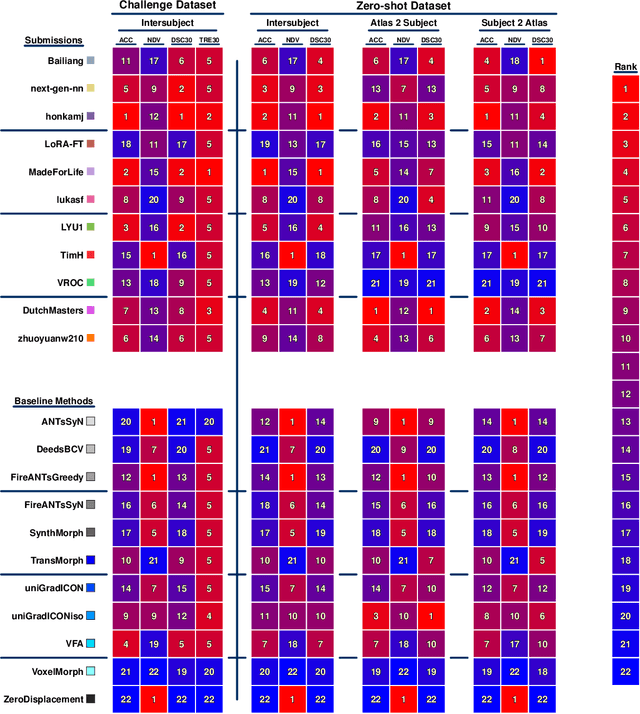
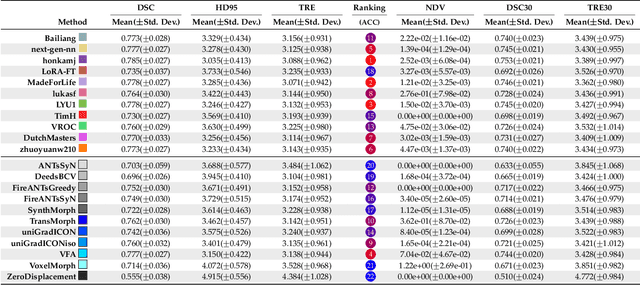
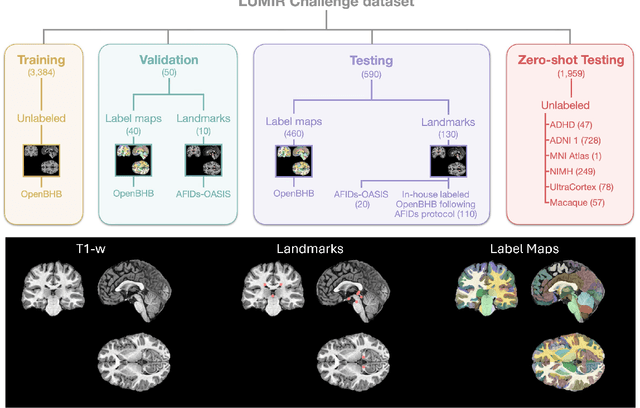
Medical image challenges have played a transformative role in advancing the field, catalyzing algorithmic innovation and establishing new performance standards across diverse clinical applications. Image registration, a foundational task in neuroimaging pipelines, has similarly benefited from the Learn2Reg initiative. Building on this foundation, we introduce the Large-scale Unsupervised Brain MRI Image Registration (LUMIR) challenge, a next-generation benchmark designed to assess and advance unsupervised brain MRI registration. Distinct from prior challenges that leveraged anatomical label maps for supervision, LUMIR removes this dependency by providing over 4,000 preprocessed T1-weighted brain MRIs for training without any label maps, encouraging biologically plausible deformation modeling through self-supervision. In addition to evaluating performance on 590 held-out test subjects, LUMIR introduces a rigorous suite of zero-shot generalization tasks, spanning out-of-domain imaging modalities (e.g., FLAIR, T2-weighted, T2*-weighted), disease populations (e.g., Alzheimer's disease), acquisition protocols (e.g., 9.4T MRI), and species (e.g., macaque brains). A total of 1,158 subjects and over 4,000 image pairs were included for evaluation. Performance was assessed using both segmentation-based metrics (Dice coefficient, 95th percentile Hausdorff distance) and landmark-based registration accuracy (target registration error). Across both in-domain and zero-shot tasks, deep learning-based methods consistently achieved state-of-the-art accuracy while producing anatomically plausible deformation fields. The top-performing deep learning-based models demonstrated diffeomorphic properties and inverse consistency, outperforming several leading optimization-based methods, and showing strong robustness to most domain shifts, the exception being a drop in performance on out-of-domain contrasts.

Pretraining Deformable Image Registration Networks with Random Images

Recent advances in deep learning-based medical image registration have shown that training deep neural networks~(DNNs) does not necessarily require medical images. Previous work showed that DNNs trained on randomly generated images with carefully designed noise and contrast properties can still generalize well to unseen medical data. Building on this insight, we propose using registration between random images as a proxy task for pretraining a foundation model for image registration. Empirical results show that our pretraining strategy improves registration accuracy, reduces the amount of domain-specific data needed to achieve competitive performance, and accelerates convergence during downstream training, thereby enhancing computational efficiency.

Brightness-Invariant Tracking Estimation in Tagged MRI

Magnetic resonance (MR) tagging is an imaging technique for noninvasively tracking tissue motion in vivo by creating a visible pattern of magnetization saturation (tags) that deforms with the tissue. Due to longitudinal relaxation and progression to steady-state, the tags and tissue brightnesses change over time, which makes tracking with optical flow methods error-prone. Although Fourier methods can alleviate these problems, they are also sensitive to brightness changes as well as spectral spreading due to motion. To address these problems, we introduce the brightness-invariant tracking estimation (BRITE) technique for tagged MRI. BRITE disentangles the anatomy from the tag pattern in the observed tagged image sequence and simultaneously estimates the Lagrangian motion. The inherent ill-posedness of this problem is addressed by leveraging the expressive power of denoising diffusion probabilistic models to represent the probabilistic distribution of the underlying anatomy and the flexibility of physics-informed neural networks to estimate biologically-plausible motion. A set of tagged MR images of a gel phantom was acquired with various tag periods and imaging flip angles to demonstrate the impact of brightness variations and to validate our method. The results show that BRITE achieves more accurate motion and strain estimates as compared to other state of the art methods, while also being resistant to tag fading.

Correlation Ratio for Unsupervised Learning of Multi-modal Deformable Registration

In recent years, unsupervised learning for deformable image registration has been a major research focus. This approach involves training a registration network using pairs of moving and fixed images, along with a loss function that combines an image similarity measure and deformation regularization. For multi-modal image registration tasks, the correlation ratio has been a widely-used image similarity measure historically, yet it has been underexplored in current deep learning methods. Here, we propose a differentiable correlation ratio to use as a loss function for learning-based multi-modal deformable image registration. This approach extends the traditionally non-differentiable implementation of the correlation ratio by using the Parzen windowing approximation, enabling backpropagation with deep neural networks. We validated the proposed correlation ratio on a multi-modal neuroimaging dataset. In addition, we established a Bayesian training framework to study how the trade-off between the deformation regularizer and similarity measures, including mutual information and our proposed correlation ratio, affects the registration performance.

ECLARE: Efficient cross-planar learning for anisotropic resolution enhancement

In clinical imaging, magnetic resonance (MR) image volumes are often acquired as stacks of 2D slices, permitting decreased scan times, improved signal-to-noise ratio, and image contrasts unique to 2D MR pulse sequences. While this is sufficient for clinical evaluation, automated algorithms designed for 3D analysis perform sub-optimally on 2D-acquired scans, especially those with thick slices and gaps between slices. Super-resolution (SR) methods aim to address this problem, but previous methods do not address all of the following: slice profile shape estimation, slice gap, domain shift, and non-integer / arbitrary upsampling factors. In this paper, we propose ECLARE (Efficient Cross-planar Learning for Anisotropic Resolution Enhancement), a self-SR method that addresses each of these factors. ECLARE estimates the slice profile from the 2D-acquired multi-slice MR volume, trains a network to learn the mapping from low-resolution to high-resolution in-plane patches from the same volume, and performs SR with anti-aliasing. We compared ECLARE to cubic B-spline interpolation, SMORE, and other contemporary SR methods. We used realistic and representative simulations so that quantitative performance against a ground truth could be computed, and ECLARE outperformed all other methods in both signal recovery and downstream tasks. On real data for which there is no ground truth, ECLARE demonstrated qualitative superiority over other methods as well. Importantly, as ECLARE does not use external training data it cannot suffer from domain shift between training and testing. Our code is open-source and available at https://www.github.com/sremedios/eclare.

Unsupervised learning of spatially varying regularization for diffeomorphic image registration

Spatially varying regularization accommodates the deformation variations that may be necessary for different anatomical regions during deformable image registration. Historically, optimization-based registration models have harnessed spatially varying regularization to address anatomical subtleties. However, most modern deep learning-based models tend to gravitate towards spatially invariant regularization, wherein a homogenous regularization strength is applied across the entire image, potentially disregarding localized variations. In this paper, we propose a hierarchical probabilistic model that integrates a prior distribution on the deformation regularization strength, enabling the end-to-end learning of a spatially varying deformation regularizer directly from the data. The proposed method is straightforward to implement and easily integrates with various registration network architectures. Additionally, automatic tuning of hyperparameters is achieved through Bayesian optimization, allowing efficient identification of optimal hyperparameters for any given registration task. Comprehensive evaluations on publicly available datasets demonstrate that the proposed method significantly improves registration performance and enhances the interpretability of deep learning-based registration, all while maintaining smooth deformations.

Unique MS Lesion Identification from MRI

Unique identification of multiple sclerosis (MS) white matter lesions (WMLs) is important to help characterize MS progression. WMLs are routinely identified from magnetic resonance images (MRIs) but the resultant total lesion load does not correlate well with EDSS; whereas mean unique lesion volume has been shown to correlate with EDSS. Our approach builds on prior work by incorporating Hessian matrix computation from lesion probability maps before using the random walker algorithm to estimate the volume of each unique lesion. Synthetic images demonstrate our ability to accurately count the number of lesions present. The takeaways, are: 1) that our method correctly identifies all lesions including many that are missed by previous methods; 2) we can better separate confluent lesions; and 3) we can accurately capture the total volume of WMLs in a given probability map. This work will allow new more meaningful statistics to be computed from WMLs in brain MRIs

Unsupervised Learning of Multi-modal Affine Registration for PET/CT

Affine registration plays a crucial role in PET/CT imaging, where aligning PET with CT images is challenging due to their respective functional and anatomical representations. Despite the significant promise shown by recent deep learning (DL)-based methods in various medical imaging applications, their application to multi-modal PET/CT affine registration remains relatively unexplored. This study investigates a DL-based approach for PET/CT affine registration. We introduce a novel method using Parzen windowing to approximate the correlation ratio, which acts as the image similarity measure for training DNNs in multi-modal registration. Additionally, we propose a multi-scale, instance-specific optimization scheme that iteratively refines the DNN-generated affine parameters across multiple image resolutions. Our method was evaluated against the widely used mutual information metric and a popular optimization-based technique from the ANTs package, using a large public FDG-PET/CT dataset with synthetic affine transformations. Our approach achieved a mean Dice Similarity Coefficient (DSC) of 0.870, outperforming the compared methods and demonstrating its effectiveness in multi-modal PET/CT image registration.

From Registration Uncertainty to Segmentation Uncertainty

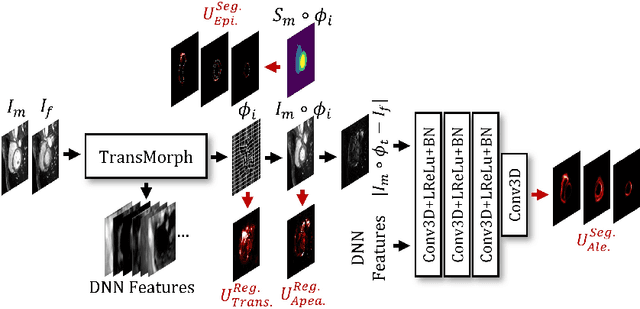
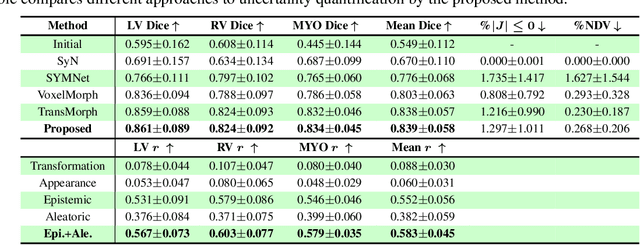
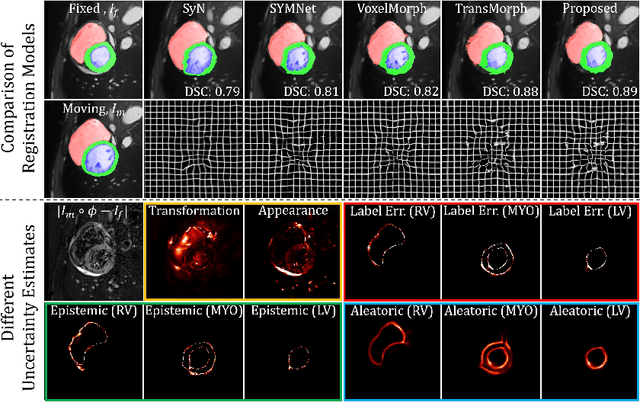
Understanding the uncertainty inherent in deep learning-based image registration models has been an ongoing area of research. Existing methods have been developed to quantify both transformation and appearance uncertainties related to the registration process, elucidating areas where the model may exhibit ambiguity regarding the generated deformation. However, our study reveals that neither uncertainty effectively estimates the potential errors when the registration model is used for label propagation. Here, we propose a novel framework to concurrently estimate both the epistemic and aleatoric segmentation uncertainties for image registration. To this end, we implement a compact deep neural network (DNN) designed to transform the appearance discrepancy in the warping into aleatoric segmentation uncertainty by minimizing a negative log-likelihood loss function. Furthermore, we present epistemic segmentation uncertainty within the label propagation process as the entropy of the propagated labels. By introducing segmentation uncertainty along with existing methods for estimating registration uncertainty, we offer vital insights into the potential uncertainties at different stages of image registration. We validated our proposed framework using publicly available datasets, and the results prove that the segmentation uncertainties estimated with the proposed method correlate well with errors in label propagation, all while achieving superior registration performance.

Is Registering Raw Tagged-MR Enough for Strain Estimation in the Era of Deep Learning?

Magnetic Resonance Imaging with tagging (tMRI) has long been utilized for quantifying tissue motion and strain during deformation. However, a phenomenon known as tag fading, a gradual decrease in tag visibility over time, often complicates post-processing. The first contribution of this study is to model tag fading by considering the interplay between $T_1$ relaxation and the repeated application of radio frequency (RF) pulses during serial imaging sequences. This is a factor that has been overlooked in prior research on tMRI post-processing. Further, we have observed an emerging trend of utilizing raw tagged MRI within a deep learning-based (DL) registration framework for motion estimation. In this work, we evaluate and analyze the impact of commonly used image similarity objectives in training DL registrations on raw tMRI. This is then compared with the Harmonic Phase-based approach, a traditional approach which is claimed to be robust to tag fading. Our findings, derived from both simulated images and an actual phantom scan, reveal the limitations of various similarity losses in raw tMRI and emphasize caution in registration tasks where image intensity changes over time.