Minimizing Live Experiments in Recommender Systems: User Simulation to Evaluate Preference Elicitation Policies

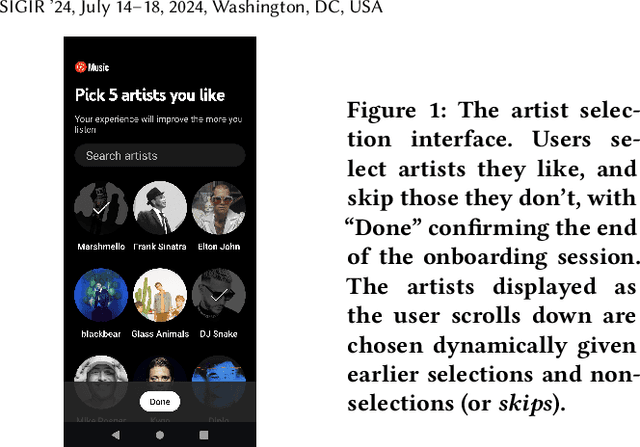
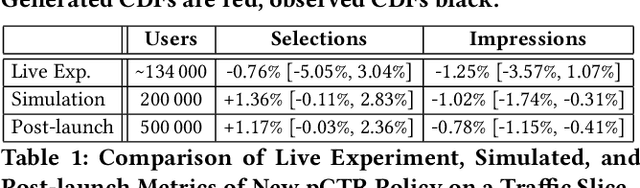
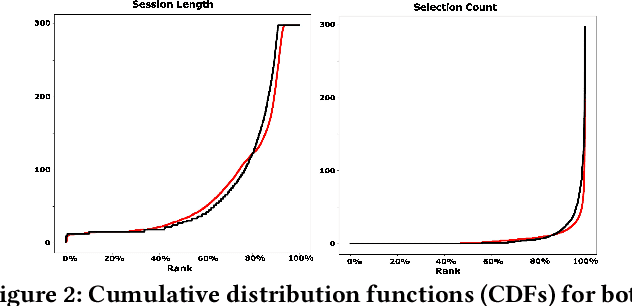
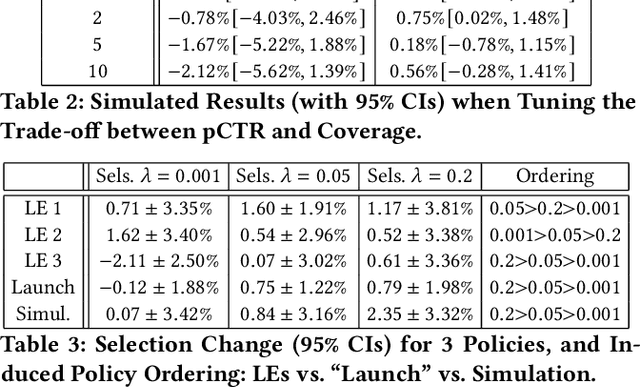
Evaluation of policies in recommender systems typically involves A/B testing using live experiments on real users to assess a new policy's impact on relevant metrics. This ``gold standard'' comes at a high cost, however, in terms of cycle time, user cost, and potential user retention. In developing policies for ``onboarding'' new users, these costs can be especially problematic, since on-boarding occurs only once. In this work, we describe a simulation methodology used to augment (and reduce) the use of live experiments. We illustrate its deployment for the evaluation of ``preference elicitation'' algorithms used to onboard new users of the YouTube Music platform. By developing counterfactually robust user behavior models, and a simulation service that couples such models with production infrastructure, we are able to test new algorithms in a way that reliably predicts their performance on key metrics when deployed live. We describe our domain, our simulation models and platform, results of experiments and deployment, and suggest future steps needed to further realistic simulation as a powerful complement to live experiments.

Density-based User Representation through Gaussian Process Regression for Multi-interest Personalized Retrieval

Accurate modeling of the diverse and dynamic interests of users remains a significant challenge in the design of personalized recommender systems. Existing user modeling methods, like single-point and multi-point representations, have limitations w.r.t. accuracy, diversity, computational cost, and adaptability. To overcome these deficiencies, we introduce density-based user representations (DURs), a novel model that leverages Gaussian process regression for effective multi-interest recommendation and retrieval. Our approach, GPR4DUR, exploits DURs to capture user interest variability without manual tuning, incorporates uncertainty-awareness, and scales well to large numbers of users. Experiments using real-world offline datasets confirm the adaptability and efficiency of GPR4DUR, while online experiments with simulated users demonstrate its ability to address the exploration-exploitation trade-off by effectively utilizing model uncertainty.

Overcoming Prior Misspecification in Online Learning to Rank

The recent literature on online learning to rank (LTR) has established the utility of prior knowledge to Bayesian ranking bandit algorithms. However, a major limitation of existing work is the requirement for the prior used by the algorithm to match the true prior. In this paper, we propose and analyze adaptive algorithms that address this issue and additionally extend these results to the linear and generalized linear models. We also consider scalar relevance feedback on top of click feedback. Moreover, we demonstrate the efficacy of our algorithms using both synthetic and real-world experiments.

Advantage Amplification in Slowly Evolving Latent-State Environments

Latent-state environments with long horizons, such as those faced by recommender systems, pose significant challenges for reinforcement learning (RL). In this work, we identify and analyze several key hurdles for RL in such environments, including belief state error and small action advantage. We develop a general principle of advantage amplification that can overcome these hurdles through the use of temporal abstraction. We propose several aggregation methods and prove they induce amplification in certain settings. We also bound the loss in optimality incurred by our methods in environments where latent state evolves slowly and demonstrate their performance empirically in a stylized user-modeling task.

Empirical Bayes Regret Minimization

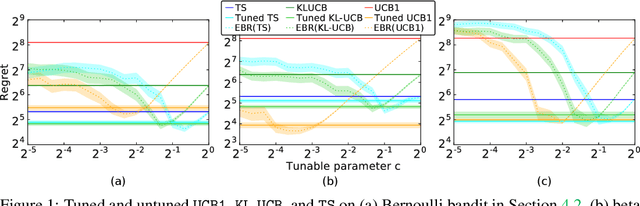
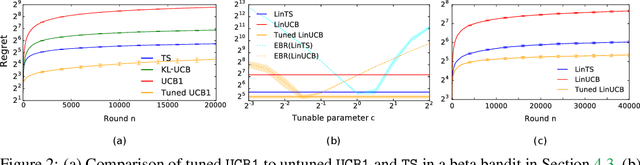
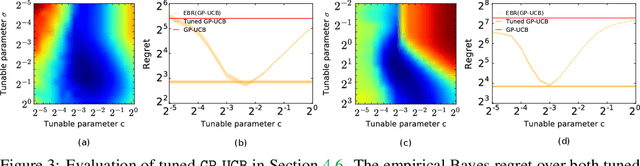
The prevalent approach to bandit algorithm design is to have a low-regret algorithm by design. While celebrated, this approach is often conservative because it ignores many intricate properties of actual problem instances. In this work, we pioneer the idea of minimizing an empirical approximation to the Bayes regret, the expected regret with respect to a distribution over problems. This approach can be viewed as an instance of learning-to-learn, it is conceptually straightforward, and easy to implement. We conduct a comprehensive empirical study of empirical Bayes regret minimization in a wide range of bandit problems, from Bernoulli bandits to structured problems, such as generalized linear and Gaussian process bandits. We report significant improvements over state-of-the-art bandit algorithms, often by an order of magnitude, by simply optimizing over a sample from the distribution.

Deep Structured Prediction with Nonlinear Output Transformations

Deep structured models are widely used for tasks like semantic segmentation, where explicit correlations between variables provide important prior information which generally helps to reduce the data needs of deep nets. However, current deep structured models are restricted by oftentimes very local neighborhood structure, which cannot be increased for computational complexity reasons, and by the fact that the output configuration, or a representation thereof, cannot be transformed further. Very recent approaches which address those issues include graphical model inference inside deep nets so as to permit subsequent non-linear output space transformations. However, optimization of those formulations is challenging and not well understood. Here, we develop a novel model which generalizes existing approaches, such as structured prediction energy networks, and discuss a formulation which maintains applicability of existing inference techniques.

Seq2Slate: Re-ranking and Slate Optimization with RNNs

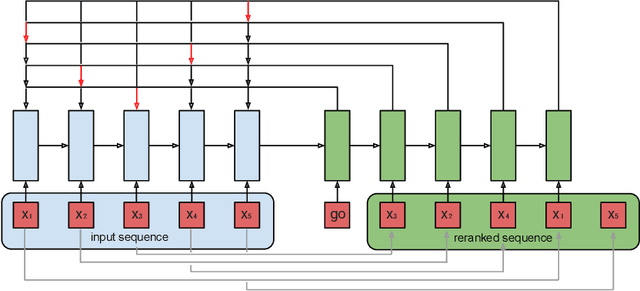
Ranking is a central task in machine learning and information retrieval. In this task, it is especially important to present the user with a slate of items that is appealing as a whole. This in turn requires taking into account interactions between items, since intuitively, placing an item on the slate affects the decision of which other items should be placed alongside it. In this work, we propose a sequence-to-sequence model for ranking called seq2slate. At each step, the model predicts the next item to place on the slate given the items already selected. The recurrent nature of the model allows complex dependencies between items to be captured directly in a flexible and scalable way. We show how to learn the model end-to-end from weak supervision in the form of easily obtained click-through data. We further demonstrate the usefulness of our approach in experiments on standard ranking benchmarks as well as in a real-world recommendation system.

Planning and Learning with Stochastic Action Sets

In many practical uses of reinforcement learning (RL) the set of actions available at a given state is a random variable, with realizations governed by an exogenous stochastic process. Somewhat surprisingly, the foundations for such sequential decision processes have been unaddressed. In this work, we formalize and investigate MDPs with stochastic action sets (SAS-MDPs) to provide these foundations. We show that optimal policies and value functions in this model have a structure that admits a compact representation. From an RL perspective, we show that Q-learning with sampled action sets is sound. In model-based settings, we consider two important special cases: when individual actions are available with independent probabilities; and a sampling-based model for unknown distributions. We develop poly-time value and policy iteration methods for both cases; and in the first, we offer a poly-time linear programming solution.

Linear-memory and Decomposition-invariant Linearly Convergent Conditional Gradient Algorithm for Structured Polytopes

Recently, several works have shown that natural modifications of the classical conditional gradient method (aka Frank-Wolfe algorithm) for constrained convex optimization, provably converge with a linear rate when: i) the feasible set is a polytope, and ii) the objective is smooth and strongly-convex. However, all of these results suffer from two significant shortcomings: large memory requirement due to the need to store an explicit convex decomposition of the current iterate, and as a consequence, large running-time overhead per iteration, and worst case convergence rate that depends unfavorably on the dimension. In this work we present a new conditional gradient variant and a corresponding analysis that improves on both of the above shortcomings. In particular: both memory and computation overheads are only linear in the dimension. Moreover, in case the optimal solution is sparse, the new convergence rate replaces a factor which is at least linear in the dimension in previous works, with a linear dependence on the number of non-zeros in the optimal solution. At the heart of our method, and corresponding analysis, is a novel way to compute decomposition-invariant away-steps. While our theoretical guarantees do not apply to any polytope, they apply to several important structured polytopes that capture central concepts such as paths in graphs, perfect matchings in bipartite graphs, marginal distributions that arise in structured prediction tasks, and more. Our theoretical findings are complemented by empirical evidence which shows that our method delivers state-of-the-art performance.

Train and Test Tightness of LP Relaxations in Structured Prediction

Structured prediction is used in areas such as computer vision and natural language processing to predict structured outputs such as segmentations or parse trees. In these settings, prediction is performed by MAP inference or, equivalently, by solving an integer linear program. Because of the complex scoring functions required to obtain accurate predictions, both learning and inference typically require the use of approximate solvers. We propose a theoretical explanation to the striking observation that approximations based on linear programming (LP) relaxations are often tight on real-world instances. In particular, we show that learning with LP relaxed inference encourages integrality of training instances, and that tightness generalizes from train to test data.