CMPhysBench: A Benchmark for Evaluating Large Language Models in Condensed Matter Physics

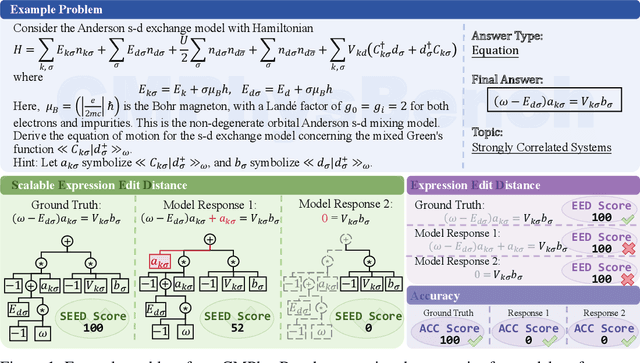
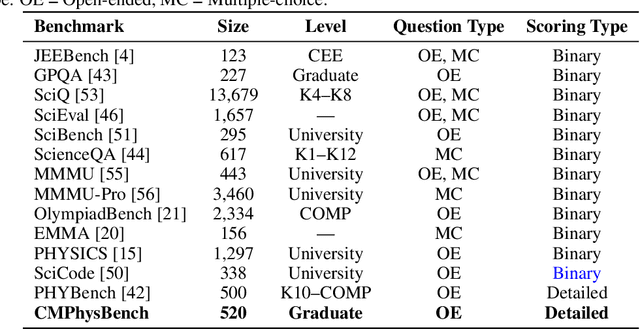
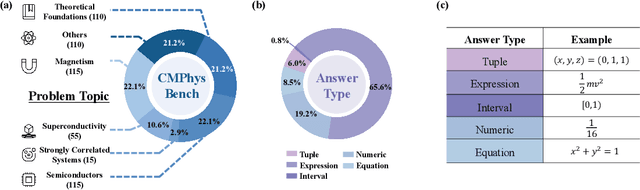
We introduce CMPhysBench, designed to assess the proficiency of Large Language Models (LLMs) in Condensed Matter Physics, as a novel Benchmark. CMPhysBench is composed of more than 520 graduate-level meticulously curated questions covering both representative subfields and foundational theoretical frameworks of condensed matter physics, such as magnetism, superconductivity, strongly correlated systems, etc. To ensure a deep understanding of the problem-solving process,we focus exclusively on calculation problems, requiring LLMs to independently generate comprehensive solutions. Meanwhile, leveraging tree-based representations of expressions, we introduce the Scalable Expression Edit Distance (SEED) score, which provides fine-grained (non-binary) partial credit and yields a more accurate assessment of similarity between prediction and ground-truth. Our results show that even the best models, Grok-4, reach only 36 average SEED score and 28% accuracy on CMPhysBench, underscoring a significant capability gap, especially for this practical and frontier domain relative to traditional physics. The code anddataset are publicly available at https://github.com/CMPhysBench/CMPhysBench.

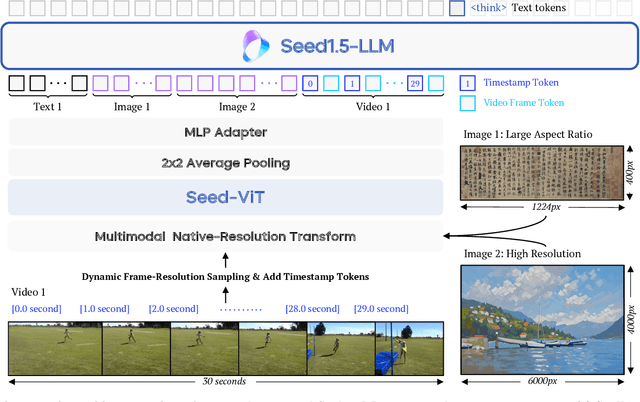
Seed1.5-VL Technical Report

We present Seed1.5-VL, a vision-language foundation model designed to advance general-purpose multimodal understanding and reasoning. Seed1.5-VL is composed with a 532M-parameter vision encoder and a Mixture-of-Experts (MoE) LLM of 20B active parameters. Despite its relatively compact architecture, it delivers strong performance across a wide spectrum of public VLM benchmarks and internal evaluation suites, achieving the state-of-the-art performance on 38 out of 60 public benchmarks. Moreover, in agent-centric tasks such as GUI control and gameplay, Seed1.5-VL outperforms leading multimodal systems, including OpenAI CUA and Claude 3.7. Beyond visual and video understanding, it also demonstrates strong reasoning abilities, making it particularly effective for multimodal reasoning challenges such as visual puzzles. We believe these capabilities will empower broader applications across diverse tasks. In this report, we mainly provide a comprehensive review of our experiences in building Seed1.5-VL across model design, data construction, and training at various stages, hoping that this report can inspire further research. Seed1.5-VL is now accessible at https://www.volcengine.com/ (Volcano Engine Model ID: doubao-1-5-thinking-vision-pro-250428)

Towards Robust Time-of-Flight Depth Denoising with Confidence-Aware Diffusion Model

Time-of-Flight (ToF) sensors efficiently capture scene depth, but the nonlinear depth construction procedure often results in extremely large noise variance or even invalid areas. Recent methods based on deep neural networks (DNNs) achieve enhanced ToF denoising accuracy but tend to struggle when presented with severe noise corruption due to limited prior knowledge of ToF data distribution. In this paper, we propose DepthCAD, a novel ToF denoising approach that ensures global structural smoothness by leveraging the rich prior knowledge in Stable Diffusion and maintains local metric accuracy by steering the diffusion process with confidence guidance. To adopt the pretrained image diffusion model to ToF depth denoising, we apply the diffusion on raw ToF correlation measurements with dynamic range normalization before converting to depth maps. Experimental results validate the state-of-the-art performance of the proposed scheme, and the evaluation on real data further verifies its robustness against real-world ToF noise.

URSA: Understanding and Verifying Chain-of-thought Reasoning in Multimodal Mathematics

Chain-of-thought (CoT) reasoning has been widely applied in the mathematical reasoning of Large Language Models (LLMs). Recently, the introduction of derivative process supervision on CoT trajectories has sparked discussions on enhancing scaling capabilities during test time, thereby boosting the potential of these models. However, in multimodal mathematical reasoning, the scarcity of high-quality CoT training data has hindered existing models from achieving high-precision CoT reasoning and has limited the realization of reasoning potential during test time. In this work, we propose a three-module synthesis strategy that integrates CoT distillation, trajectory-format rewriting, and format unification. It results in a high-quality CoT reasoning instruction fine-tuning dataset in multimodal mathematics, MMathCoT-1M. We comprehensively validate the state-of-the-art (SOTA) performance of the trained URSA-7B model on multiple multimodal mathematical benchmarks. For test-time scaling, we introduce a data synthesis strategy that automatically generates process annotation datasets, known as DualMath-1.1M, focusing on both interpretation and logic. By further training URSA-7B on DualMath-1.1M, we transition from CoT reasoning capabilities to robust supervision abilities. The trained URSA-RM-7B acts as a verifier, effectively enhancing the performance of URSA-7B at test time. URSA-RM-7B also demonstrates excellent out-of-distribution (OOD) verifying capabilities, showcasing its generalization. Model weights, training data and code will be open-sourced.

Math-PUMA: Progressive Upward Multimodal Alignment to Enhance Mathematical Reasoning

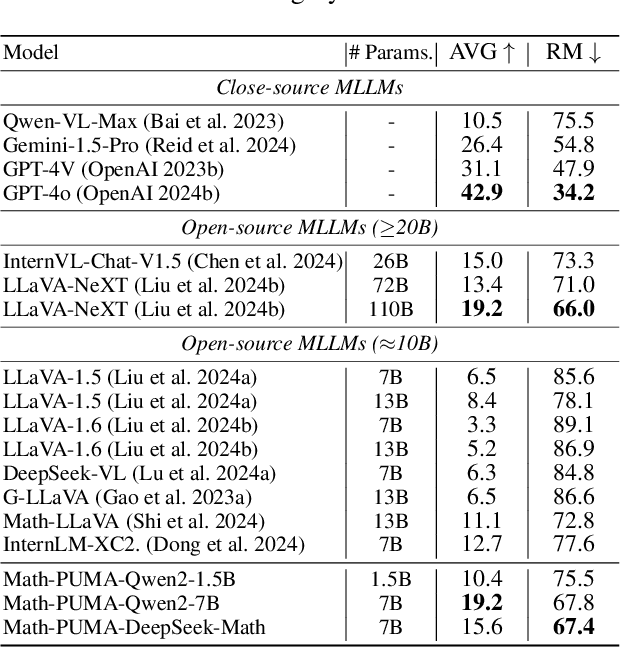
Multimodal Large Language Models (MLLMs) excel in solving text-based mathematical problems, but they struggle with mathematical diagrams since they are primarily trained on natural scene images. For humans, visual aids generally enhance problem-solving, but MLLMs perform worse as information shifts from textual to visual modality. This decline is mainly due to their shortcomings in aligning images and text. To tackle aforementioned challenges, we propose Math-PUMA, a methodology focused on Progressive Upward Multimodal Alignment. This approach is designed to improve the mathematical reasoning skills of MLLMs through a three-stage training process, with the second stage being the critical alignment stage. We first enhance the language model's mathematical reasoning capabilities with extensive set of textual mathematical problems. We then construct a multimodal dataset with varying degrees of textual and visual information, creating data pairs by presenting each problem in at least two forms. By leveraging the Kullback-Leibler (KL) divergence of next-token prediction distributions to align visual and textual modalities, consistent problem-solving abilities are ensured. Finally, we utilize multimodal instruction tuning for MLLMs with high-quality multimodal data. Experimental results on multiple mathematical reasoning benchmarks demonstrate that the MLLMs trained with Math-PUMA surpass most open-source MLLMs. Our approach effectively narrows the performance gap for problems presented in different modalities.

Sparse Graph Learning with Eigen-gap for Spectral Filter Training in Graph Convolutional Networks

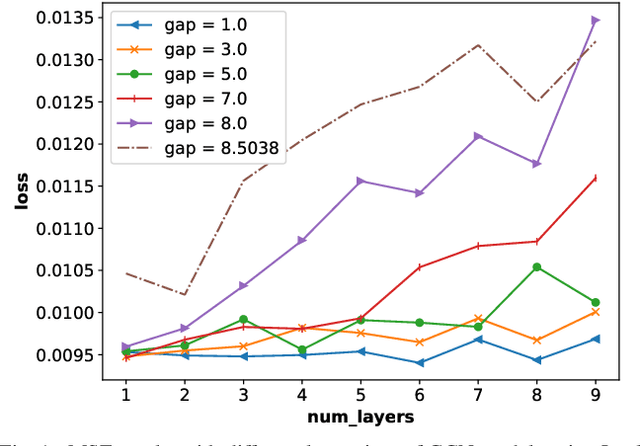
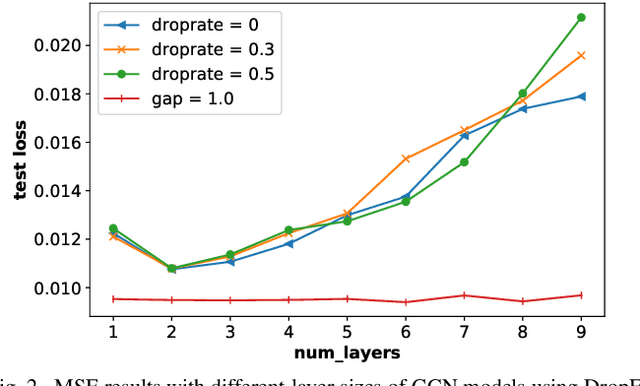
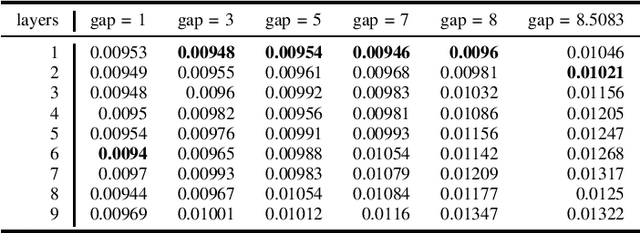
It is now known that the expressive power of graph convolutional neural nets (GCN) does not grow infinitely with the number of layers. Instead, the GCN output approaches a subspace spanned by the first eigenvector of the normalized graph Laplacian matrix with the convergence rate characterized by the "eigen-gap": the difference between the Laplacian's first two distinct eigenvalues. To promote a deeper GCN architecture with sufficient expressiveness, in this paper, given an empirical covariance matrix $\bar{C}$ computed from observable data, we learn a sparse graph Laplacian matrix $L$ closest to $\bar{C}^{-1}$ while maintaining a desirable eigen-gap that slows down convergence. Specifically, we first define a sparse graph learning problem with constraints on the first eigenvector (the most common signal) and the eigen-gap. We solve the corresponding dual problem greedily, where a locally optimal eigen-pair is computed one at a time via a fast approximation of a semi-definite programming (SDP) formulation. The computed $L$ with the desired eigen-gap is normalized spectrally and used for supervised training of GCN for a targeted task. Experiments show that our proposal produced deeper GCNs and smaller errors compared to a competing scheme without explicit eigen-gap optimization.

Towards Geometry Guided Neural Relighting with Flash Photography

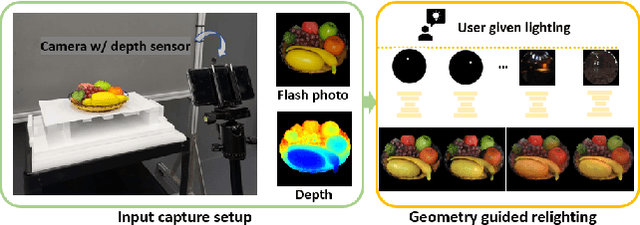
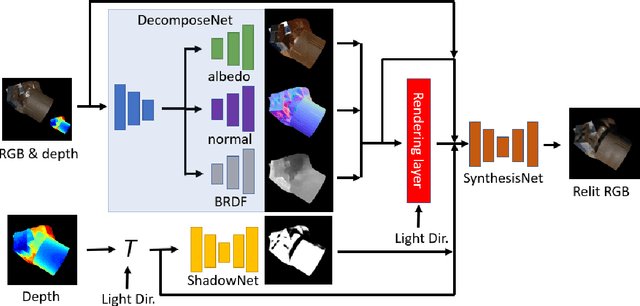
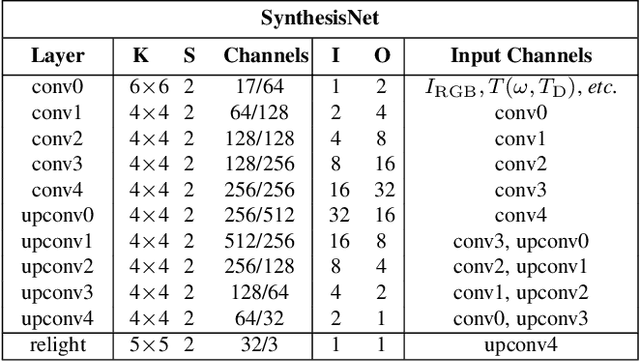
Previous image based relighting methods require capturing multiple images to acquire high frequency lighting effect under different lighting conditions, which needs nontrivial effort and may be unrealistic in certain practical use scenarios. While such approaches rely entirely on cleverly sampling the color images under different lighting conditions, little has been done to utilize geometric information that crucially influences the high-frequency features in the images, such as glossy highlight and cast shadow. We therefore propose a framework for image relighting from a single flash photograph with its corresponding depth map using deep learning. By incorporating the depth map, our approach is able to extrapolate realistic high-frequency effects under novel lighting via geometry guided image decomposition from the flashlight image, and predict the cast shadow map from the shadow-encoding transformed depth map. Moreover, the single-image based setup greatly simplifies the data capture process. We experimentally validate the advantage of our geometry guided approach over state-of-the-art image-based approaches in intrinsic image decomposition and image relighting, and also demonstrate our performance on real mobile phone photo examples.

A Self-Attention Joint Model for Spoken Language Understanding in Situational Dialog Applications

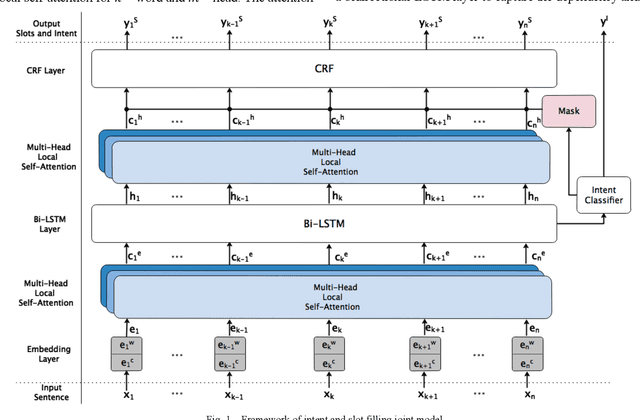
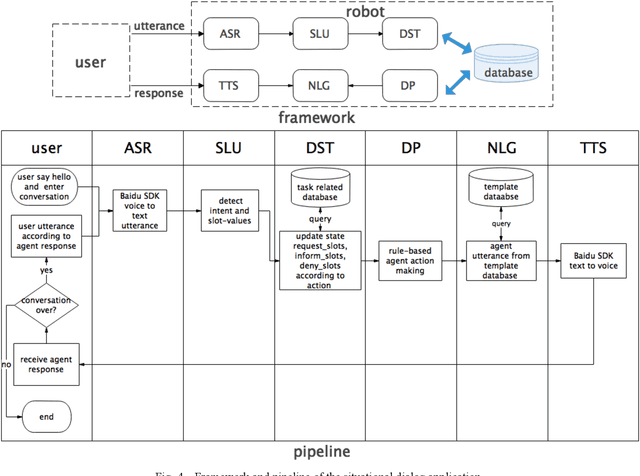
Spoken language understanding (SLU) acts as a critical component in goal-oriented dialog systems. It typically involves identifying the speakers intent and extracting semantic slots from user utterances, which are known as intent detection (ID) and slot filling (SF). SLU problem has been intensively investigated in recent years. However, these methods just constrain SF results grammatically, solve ID and SF independently, or do not fully utilize the mutual impact of the two tasks. This paper proposes a multi-head self-attention joint model with a conditional random field (CRF) layer and a prior mask. The experiments show the effectiveness of our model, as compared with state-of-the-art models. Meanwhile, online education in China has made great progress in the last few years. But there are few intelligent educational dialog applications for students to learn foreign languages. Hence, we design an intelligent dialog robot equipped with different scenario settings to help students learn communication skills.

Deep Surface Normal Estimation with Hierarchical RGB-D Fusion

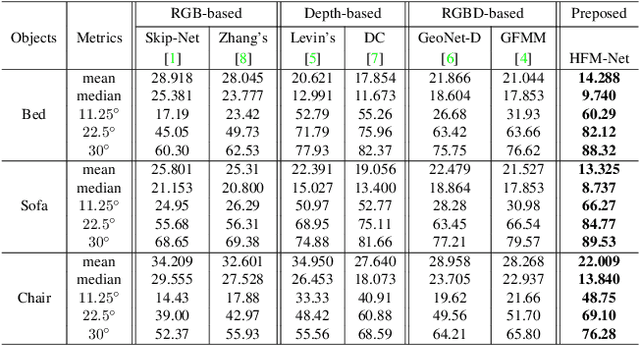
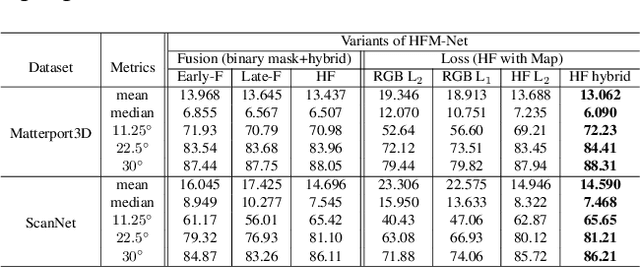
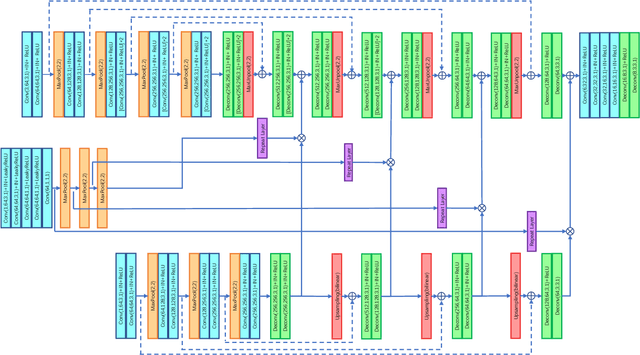
The growing availability of commodity RGB-D cameras has boosted the applications in the field of scene understanding. However, as a fundamental scene understanding task, surface normal estimation from RGB-D data lacks thorough investigation. In this paper, a hierarchical fusion network with adaptive feature re-weighting is proposed for surface normal estimation from a single RGB-D image. Specifically, the features from color image and depth are successively integrated at multiple scales to ensure global surface smoothness while preserving visually salient details. Meanwhile, the depth features are re-weighted with a confidence map estimated from depth before merging into the color branch to avoid artifacts caused by input depth corruption. Additionally, a hybrid multi-scale loss function is designed to learn accurate normal estimation given noisy ground-truth dataset. Extensive experimental results validate the effectiveness of the fusion strategy and the loss design, outperforming state-of-the-art normal estimation schemes.

Deep Graph Laplacian Regularization

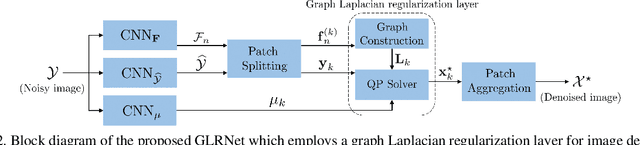
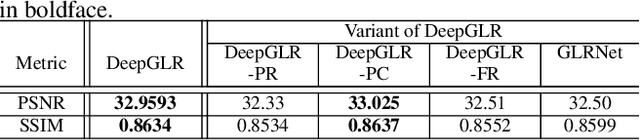
We propose to combine the robustness merit of model-based approaches and the learning power of data-driven approaches for image restoration. Specifically, by integrating graph Laplacian regularization as a trainable module into a deep learning framework, we are less susceptible to overfitting than pure CNN-based approaches, achieving higher robustness to small dataset and cross-domain denoising. First, a sparse neighborhood graph is built from the output of a convolutional neural network (CNN). Then the image is restored by solving an unconstrained quadratic programming problem, using a corresponding graph Laplacian regularizer as a prior term. The proposed restoration pipeline is fully differentiable and hence can be end-to-end trained. Experimental results demonstrate that our work avoids overfitting given small training data. It is also endowed with strong cross-domain generalization power, outperforming the state-of-the-art approaches by remarkable margin.