Graph Sparsification for GCN Towards Optimal Crop Yield Predictions

In agronomics, predicting crop yield at a per field/county granularity is important for farmers to minimize uncertainty and plan seeding for the next crop cycle. While state-of-the-art prediction techniques employ graph convolutional nets (GCN) to predict future crop yields given relevant features and crop yields of previous years, a dense underlying graph kernel requires long training and execution time. In this paper, we propose a graph sparsification method based on the Fiedler number to remove edges from a complete graph kernel, in order to lower the complexity of GCN training/execution. Specifically, we first show that greedily removing an edge at a time that induces the minimal change in the second eigenvalue leads to a sparse graph with good GCN performance. We then propose a fast method to choose an edge for removal per iteration based on an eigenvalue perturbation theorem. Experiments show that our Fiedler-based method produces a sparse graph with good GCN performance compared to other graph sparsification schemes in crop yield prediction.

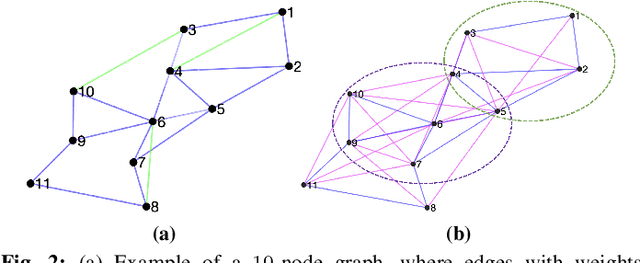
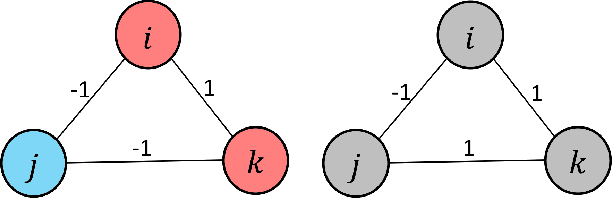
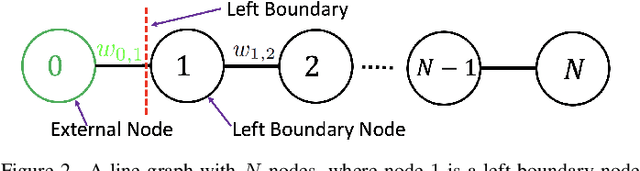
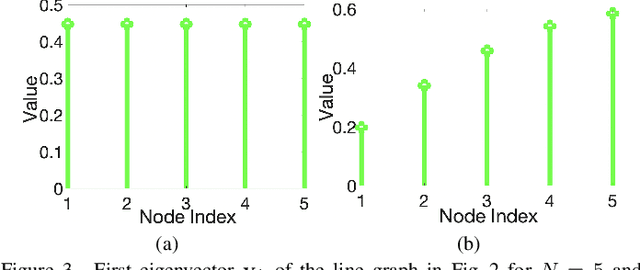
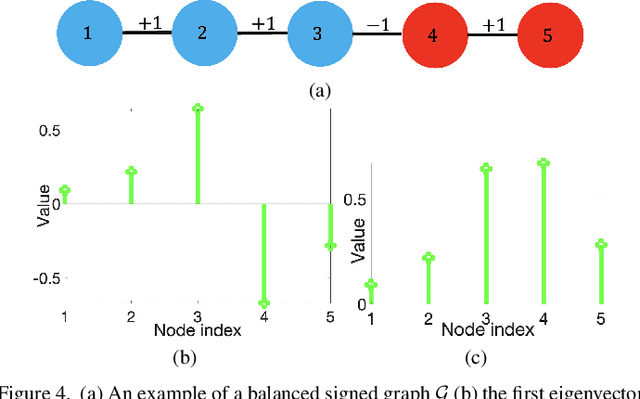
Efficient Signed Graph Sampling via Balancing & Gershgorin Disc Perfect Alignment

A basic premise in graph signal processing (GSP) is that a graph encoding pairwise (anti-)correlations of the targeted signal as edge weights is exploited for graph filtering. However, existing fast graph sampling schemes are designed and tested only for positive graphs describing positive correlations. In this paper, we show that for datasets with strong inherent anti-correlations, a suitable graph contains both positive and negative edge weights. In response, we propose a linear-time signed graph sampling method centered on the concept of balanced signed graphs. Specifically, given an empirical covariance data matrix $\bar{\bf{C}}$, we first learn a sparse inverse matrix (graph Laplacian) $\mathcal{L}$ corresponding to a signed graph $\mathcal{G}$. We define the eigenvectors of Laplacian $\mathcal{L}_B$ for a balanced signed graph $\mathcal{G}_B$ -- approximating $\mathcal{G}$ via edge weight augmentation -- as graph frequency components. Next, we choose samples to minimize the low-pass filter reconstruction error in two steps. We first align all Gershgorin disc left-ends of Laplacian $\mathcal{L}_B$ at smallest eigenvalue $\lambda_{\min}(\mathcal{L}_B)$ via similarity transform $\mathcal{L}_p = \S \mathcal{L}_B \S^{-1}$, leveraging a recent linear algebra theorem called Gershgorin disc perfect alignment (GDPA). We then perform sampling on $\mathcal{L}_p$ using a previous fast Gershgorin disc alignment sampling (GDAS) scheme. Experimental results show that our signed graph sampling method outperformed existing fast sampling schemes noticeably on various datasets.

Unsupervised Graph Spectral Feature Denoising for Crop Yield Prediction

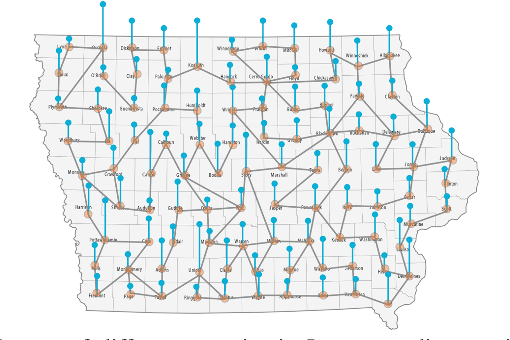
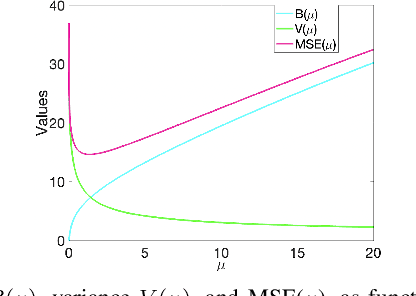
Prediction of annual crop yields at a county granularity is important for national food production and price stability. In this paper, towards the goal of better crop yield prediction, leveraging recent graph signal processing (GSP) tools to exploit spatial correlation among neighboring counties, we denoise relevant features via graph spectral filtering that are inputs to a deep learning prediction model. Specifically, we first construct a combinatorial graph with edge weights that encode county-to-county similarities in soil and location features via metric learning. We then denoise features via a maximum a posteriori (MAP) formulation with a graph Laplacian regularizer (GLR). We focus on the challenge to estimate the crucial weight parameter $\mu$, trading off the fidelity term and GLR, that is a function of noise variance in an unsupervised manner. We first estimate noise variance directly from noise-corrupted graph signals using a graph clique detection (GCD) procedure that discovers locally constant regions. We then compute an optimal $\mu$ minimizing an approximate mean square error function via bias-variance analysis. Experimental results from collected USDA data show that using denoised features as input, performance of a crop yield prediction model can be improved noticeably.

Hybrid Model-based / Data-driven Graph Transform for Image Coding

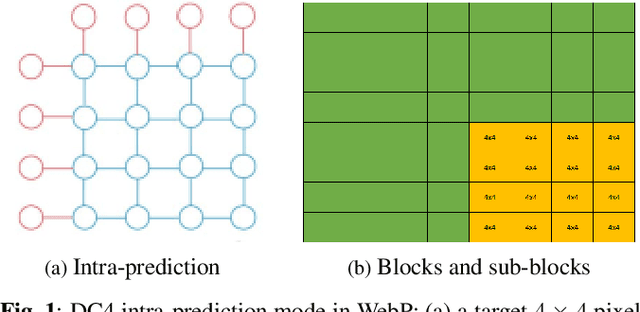
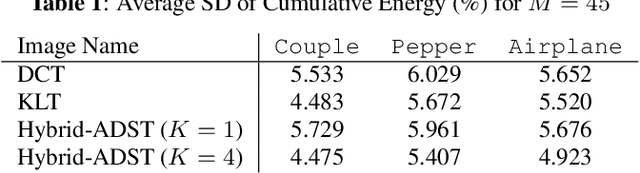
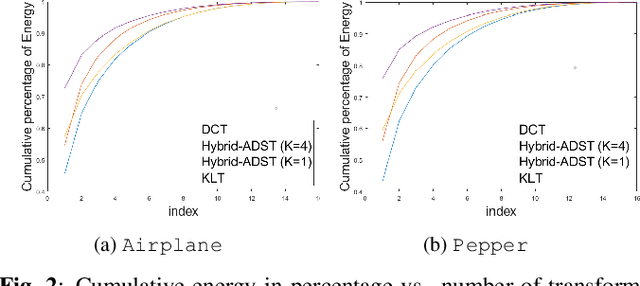
Transform coding to sparsify signal representations remains crucial in an image compression pipeline. While the Karhunen-Lo\`{e}ve transform (KLT) computed from an empirical covariance matrix $\bar{C}$ is theoretically optimal for a stationary process, in practice, collecting sufficient statistics from a non-stationary image to reliably estimate $\bar{C}$ can be difficult. In this paper, to encode an intra-prediction residual block, we pursue a hybrid model-based / data-driven approach: the first $K$ eigenvectors of a transform matrix are derived from a statistical model, e.g., the asymmetric discrete sine transform (ADST), for stability, while the remaining $N-K$ are computed from $\bar{C}$ for performance. The transform computation is posed as a graph learning problem, where we seek a graph Laplacian matrix minimizing a graphical lasso objective inside a convex cone sharing the first $K$ eigenvectors in a Hilbert space of real symmetric matrices. We efficiently solve the problem via augmented Lagrangian relaxation and proximal gradient (PG). Using WebP as a baseline image codec, experimental results show that our hybrid graph transform achieved better energy compaction than default discrete cosine transform (DCT) and better stability than KLT.

Sparse Graph Learning with Eigen-gap for Spectral Filter Training in Graph Convolutional Networks

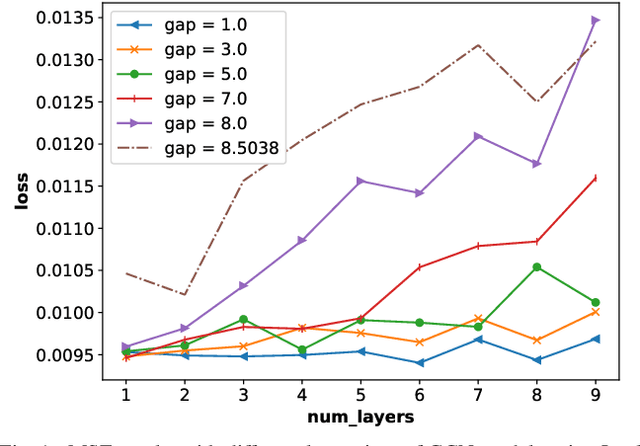
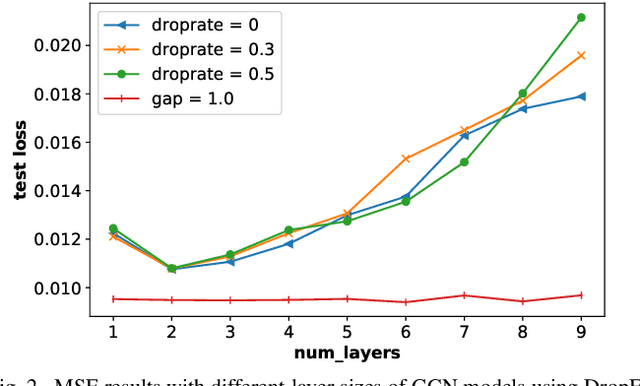
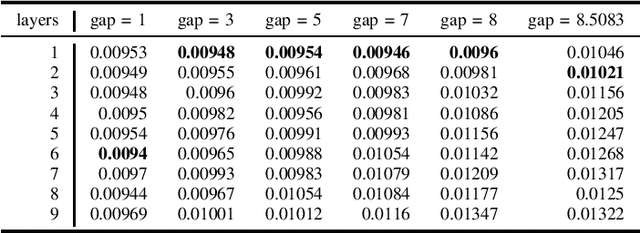
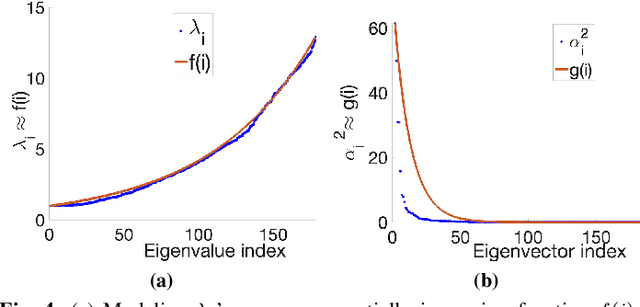
It is now known that the expressive power of graph convolutional neural nets (GCN) does not grow infinitely with the number of layers. Instead, the GCN output approaches a subspace spanned by the first eigenvector of the normalized graph Laplacian matrix with the convergence rate characterized by the "eigen-gap": the difference between the Laplacian's first two distinct eigenvalues. To promote a deeper GCN architecture with sufficient expressiveness, in this paper, given an empirical covariance matrix $\bar{C}$ computed from observable data, we learn a sparse graph Laplacian matrix $L$ closest to $\bar{C}^{-1}$ while maintaining a desirable eigen-gap that slows down convergence. Specifically, we first define a sparse graph learning problem with constraints on the first eigenvector (the most common signal) and the eigen-gap. We solve the corresponding dual problem greedily, where a locally optimal eigen-pair is computed one at a time via a fast approximation of a semi-definite programming (SDP) formulation. The computed $L$ with the desired eigen-gap is normalized spectrally and used for supervised training of GCN for a targeted task. Experiments show that our proposal produced deeper GCNs and smaller errors compared to a competing scheme without explicit eigen-gap optimization.

Learning Sparse Graph Laplacian with $K$ Eigenvector Prior via Iterative GLASSO and Projection

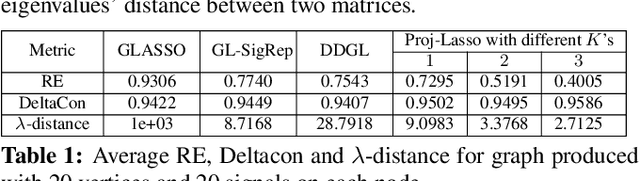
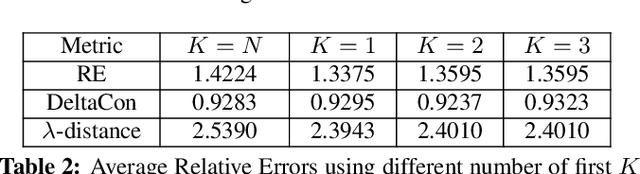
Learning a suitable graph is an important precursor to many graph signal processing (GSP) pipelines, such as graph spectral signal compression and denoising. Previous graph learning algorithms either i) make some assumptions on connectivity (e.g., graph sparsity), or ii) make simple graph edge assumptions such as positive edges only. In this paper, given an empirical covariance matrix $\bar{C}$ computed from data as input, we consider a structural assumption on the graph Laplacian matrix $L$: the first $K$ eigenvectors of $L$ are pre-selected, e.g., based on domain-specific criteria, such as computation requirement, and the remaining eigenvectors are then learned from data. One example use case is image coding, where the first eigenvector is pre-chosen to be constant, regardless of available observed data. We first prove that the subspace of symmetric positive semi-definite (PSD) matrices $H_{u}^+$ with the first $K$ eigenvectors being $\{u_k\}$ in a defined Hilbert space is a convex cone. We then construct an operator to project a given positive definite (PD) matrix $L$ to $H_{u}^+$, inspired by the Gram-Schmidt procedure. Finally, we design an efficient hybrid graphical lasso/projection algorithm to compute the most suitable graph Laplacian matrix $L^* \in H_{u}^+$ given $\bar{C}$. Experimental results show that given the first $K$ eigenvectors as a prior, our algorithm outperforms competing graph learning schemes using a variety of graph comparison metrics.