Sparse Graph Learning with Eigen-gap for Spectral Filter Training in Graph Convolutional Networks

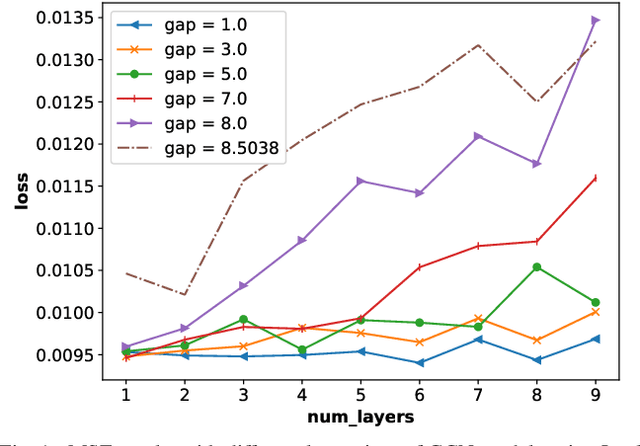
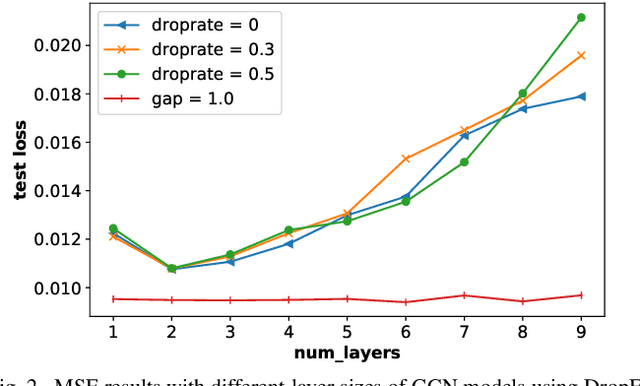
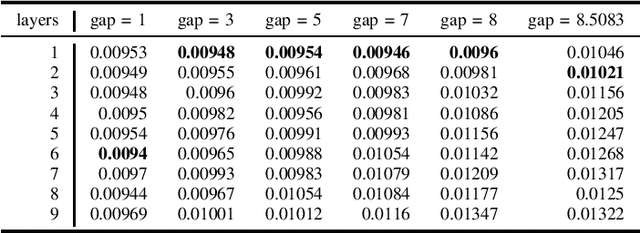
It is now known that the expressive power of graph convolutional neural nets (GCN) does not grow infinitely with the number of layers. Instead, the GCN output approaches a subspace spanned by the first eigenvector of the normalized graph Laplacian matrix with the convergence rate characterized by the "eigen-gap": the difference between the Laplacian's first two distinct eigenvalues. To promote a deeper GCN architecture with sufficient expressiveness, in this paper, given an empirical covariance matrix $\bar{C}$ computed from observable data, we learn a sparse graph Laplacian matrix $L$ closest to $\bar{C}^{-1}$ while maintaining a desirable eigen-gap that slows down convergence. Specifically, we first define a sparse graph learning problem with constraints on the first eigenvector (the most common signal) and the eigen-gap. We solve the corresponding dual problem greedily, where a locally optimal eigen-pair is computed one at a time via a fast approximation of a semi-definite programming (SDP) formulation. The computed $L$ with the desired eigen-gap is normalized spectrally and used for supervised training of GCN for a targeted task. Experiments show that our proposal produced deeper GCNs and smaller errors compared to a competing scheme without explicit eigen-gap optimization.