Complex Graph Laplacian Regularizer for Inferencing Grid States

In order to maintain stable grid operations, system monitoring and control processes require the computation of grid states (e.g. voltage magnitude and angles) at high granularity. It is necessary to infer these grid states from measurements generated by a limited number of sensors like phasor measurement units (PMUs) that can be subjected to delays and losses due to channel artefacts, and/or adversarial attacks (e.g. denial of service, jamming, etc.). We propose a novel graph signal processing (GSP) based algorithm to interpolate states of the entire grid from observations of a small number of grid measurements. It is a two-stage process, where first an underlying Hermitian graph is learnt empirically from existing grid datasets. Then, the graph is used to interpolate missing grid signal samples in linear time. With our proposal, we can effectively reconstruct grid signals with significantly smaller number of observations when compared to existing traditional approaches (e.g. state estimation). In contrast to existing GSP approaches, we do not require knowledge of the underlying grid structure and parameters and are able to guarantee fast spectral optimization. We demonstrate the computational efficacy and accuracy of our proposal via practical studies conducted on the IEEE 118 bus system.

Modeling Viral Information Spreading via Directed Acyclic Graph Diffusion

Viral information like rumors or fake news is spread over a communication network like a virus infection in a unidirectional manner: entity $i$ conveys information to a neighbor $j$, resulting in two equally informed (infected) parties. Existing graph diffusion works focus only on bidirectional diffusion on an undirected graph. Instead, we propose a new directed acyclic graph (DAG) diffusion model to estimate the probability $x_i(t)$ of node $i$'s infection at time $t$ given a source node $s$, where $x_i(\infty)~=~1$. Specifically, given an undirected positive graph modeling node-to-node communication, we first compute its graph embedding: a latent coordinate for each node in an assumed low-dimensional manifold space from extreme eigenvectors via LOBPCG. Next, we construct a DAG based on Euclidean distances between latent coordinates. Spectrally, we prove that the asymmetric DAG Laplacian matrix contains real non-negative eigenvalues, and that the DAG diffusion converges to the all-infection vector $\x(\infty) = \1$ as $t \rightarrow \infty$. Simulation experiments show that our proposed DAG diffusion accurately models viral information spreading over a variety of graph structures at different time instants.

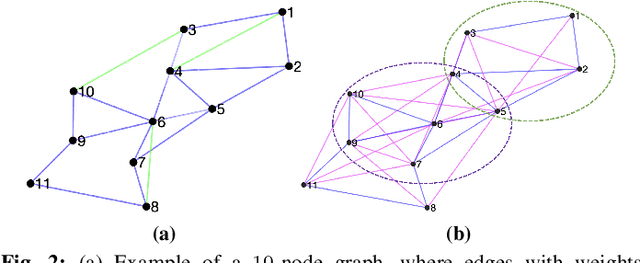
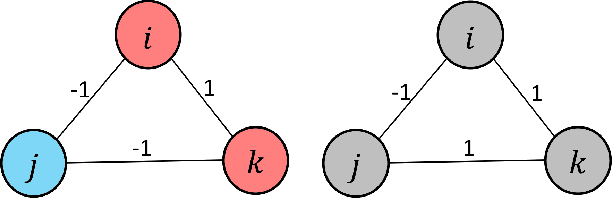
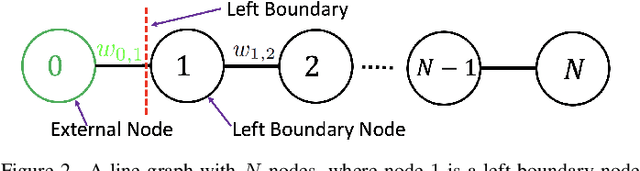
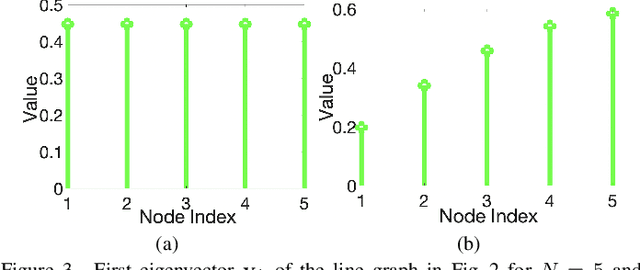
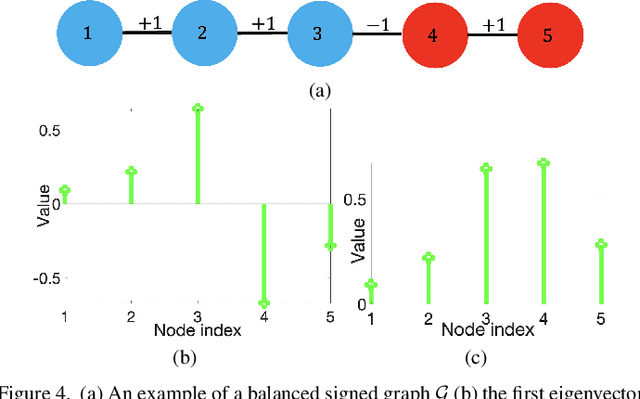
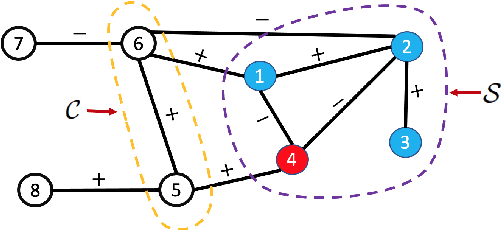
Efficient Signed Graph Sampling via Balancing & Gershgorin Disc Perfect Alignment

A basic premise in graph signal processing (GSP) is that a graph encoding pairwise (anti-)correlations of the targeted signal as edge weights is exploited for graph filtering. However, existing fast graph sampling schemes are designed and tested only for positive graphs describing positive correlations. In this paper, we show that for datasets with strong inherent anti-correlations, a suitable graph contains both positive and negative edge weights. In response, we propose a linear-time signed graph sampling method centered on the concept of balanced signed graphs. Specifically, given an empirical covariance data matrix $\bar{\bf{C}}$, we first learn a sparse inverse matrix (graph Laplacian) $\mathcal{L}$ corresponding to a signed graph $\mathcal{G}$. We define the eigenvectors of Laplacian $\mathcal{L}_B$ for a balanced signed graph $\mathcal{G}_B$ -- approximating $\mathcal{G}$ via edge weight augmentation -- as graph frequency components. Next, we choose samples to minimize the low-pass filter reconstruction error in two steps. We first align all Gershgorin disc left-ends of Laplacian $\mathcal{L}_B$ at smallest eigenvalue $\lambda_{\min}(\mathcal{L}_B)$ via similarity transform $\mathcal{L}_p = \S \mathcal{L}_B \S^{-1}$, leveraging a recent linear algebra theorem called Gershgorin disc perfect alignment (GDPA). We then perform sampling on $\mathcal{L}_p$ using a previous fast Gershgorin disc alignment sampling (GDAS) scheme. Experimental results show that our signed graph sampling method outperformed existing fast sampling schemes noticeably on various datasets.

Unsupervised Graph Spectral Feature Denoising for Crop Yield Prediction

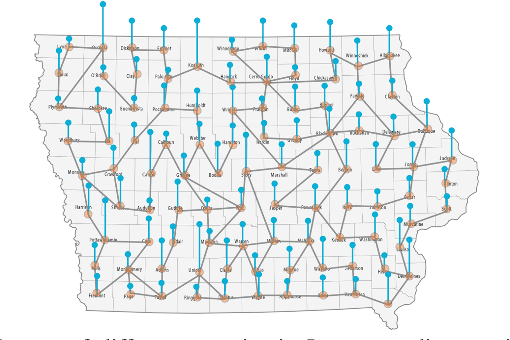
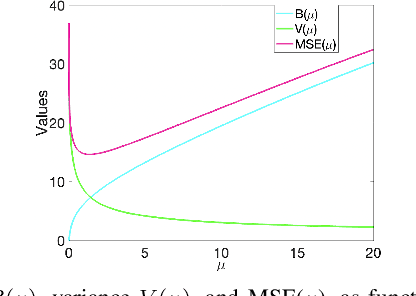
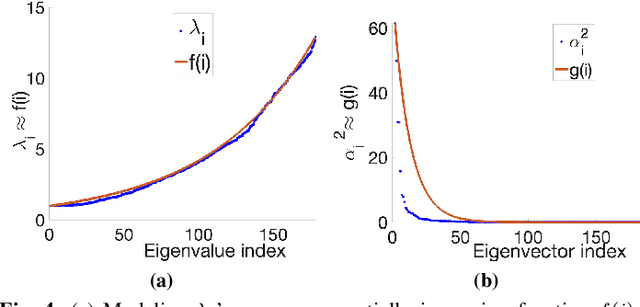
Prediction of annual crop yields at a county granularity is important for national food production and price stability. In this paper, towards the goal of better crop yield prediction, leveraging recent graph signal processing (GSP) tools to exploit spatial correlation among neighboring counties, we denoise relevant features via graph spectral filtering that are inputs to a deep learning prediction model. Specifically, we first construct a combinatorial graph with edge weights that encode county-to-county similarities in soil and location features via metric learning. We then denoise features via a maximum a posteriori (MAP) formulation with a graph Laplacian regularizer (GLR). We focus on the challenge to estimate the crucial weight parameter $\mu$, trading off the fidelity term and GLR, that is a function of noise variance in an unsupervised manner. We first estimate noise variance directly from noise-corrupted graph signals using a graph clique detection (GCD) procedure that discovers locally constant regions. We then compute an optimal $\mu$ minimizing an approximate mean square error function via bias-variance analysis. Experimental results from collected USDA data show that using denoised features as input, performance of a crop yield prediction model can be improved noticeably.

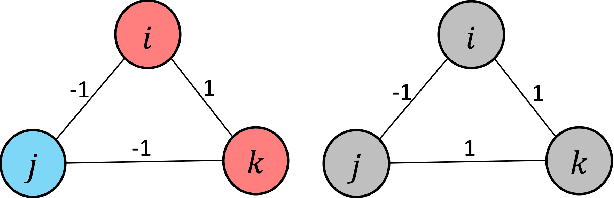
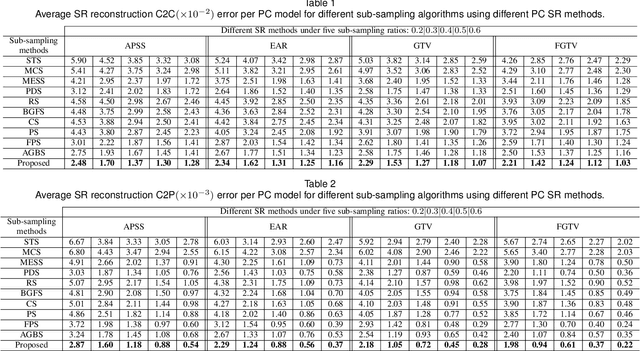
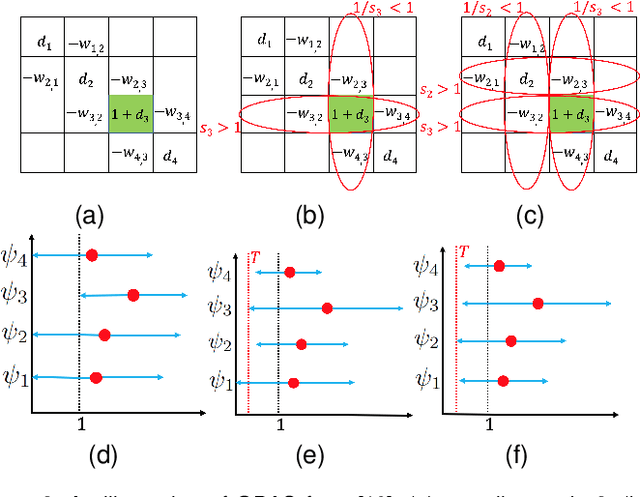
Point Cloud Sampling via Graph Balancing and Gershgorin Disc Alignment

3D point cloud (PC) -- a collection of discrete geometric samples of a physical object's surface -- is typically large in size, which entails expensive subsequent operations like viewpoint image rendering and object recognition. Leveraging on recent advances in graph sampling, we propose a fast PC sub-sampling algorithm that reduces its size while preserving the overall object shape. Specifically, to articulate a sampling objective, we first assume a super-resolution (SR) method based on feature graph Laplacian regularization (FGLR) that reconstructs the original high-resolution PC, given 3D points chosen by a sampling matrix $\H$. We prove that minimizing a worst-case SR reconstruction error is equivalent to maximizing the smallest eigenvalue $\lambda_{\min}$ of a matrix $\H^{\top} \H + \mu \cL$, where $\cL$ is a symmetric, positive semi-definite matrix computed from the neighborhood graph connecting the 3D points. Instead, for fast computation we maximize a lower bound $\lambda^-_{\min}(\H^{\top} \H + \mu \cL)$ via selection of $\H$ in three steps. Interpreting $\cL$ as a generalized graph Laplacian matrix corresponding to an unbalanced signed graph $\cG$, we first approximate $\cG$ with a balanced graph $\cG_B$ with the corresponding generalized graph Laplacian matrix $\cL_B$. Second, leveraging on a recent theorem called Gershgorin disc perfect alignment (GDPA), we perform a similarity transform $\cL_p = \S \cL_B \S^{-1}$ so that Gershgorin disc left-ends of $\cL_p$ are all aligned at the same value $\lambda_{\min}(\cL_B)$. Finally, we perform PC sub-sampling on $\cG_B$ using a graph sampling algorithm to maximize $\lambda^-_{\min}(\H^{\top} \H + \mu \cL_p)$ in roughly linear time. Experimental results show that 3D points chosen by our algorithm outperformed competing schemes both numerically and visually in SR reconstruction quality.