Ivan Bajic
Privacy-Preserving Autoencoder for Collaborative Object Detection
Feb 29, 2024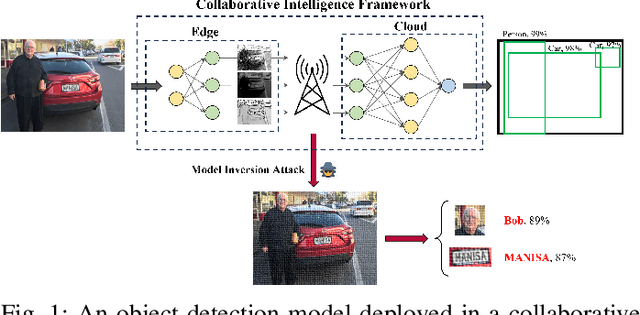
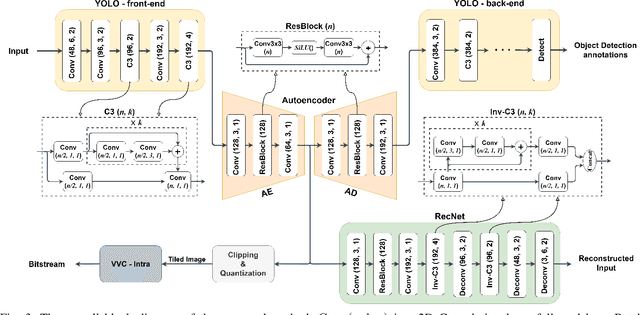

Abstract:Privacy is a crucial concern in collaborative machine vision where a part of a Deep Neural Network (DNN) model runs on the edge, and the rest is executed on the cloud. In such applications, the machine vision model does not need the exact visual content to perform its task. Taking advantage of this potential, private information could be removed from the data insofar as it does not significantly impair the accuracy of the machine vision system. In this paper, we present an autoencoder-style network integrated within an object detection pipeline, which generates a latent representation of the input image that preserves task-relevant information while removing private information. Our approach employs an adversarial training strategy that not only removes private information from the bottleneck of the autoencoder but also promotes improved compression efficiency for feature channels coded by conventional codecs like VVC-Intra. We assess the proposed system using a realistic evaluation framework for privacy, directly measuring face and license plate recognition accuracy. Experimental results show that our proposed method is able to reduce the bitrate significantly at the same object detection accuracy compared to coding the input images directly, while keeping the face and license plate recognition accuracy on the images recovered from the bottleneck features low, implying strong privacy protection.
Point Cloud Sampling via Graph Balancing and Gershgorin Disc Alignment
Mar 10, 2021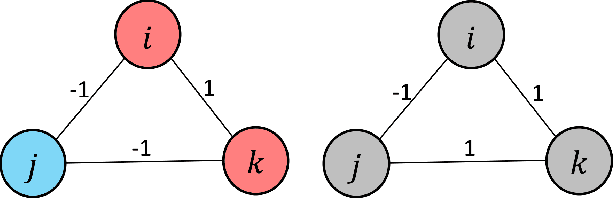
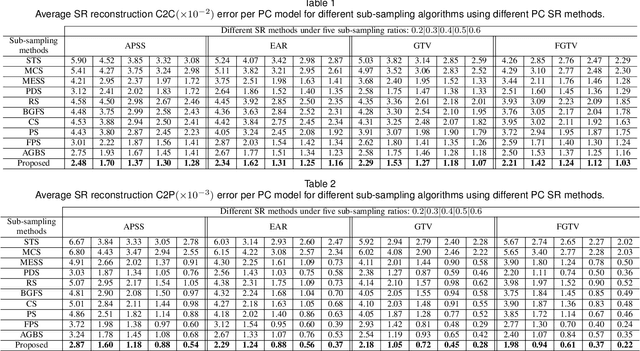
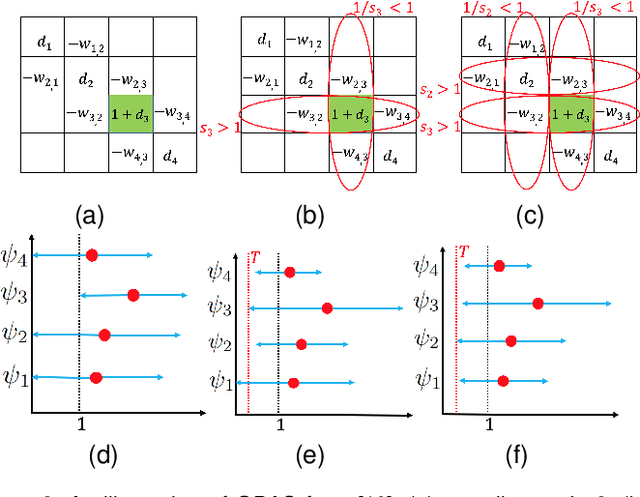
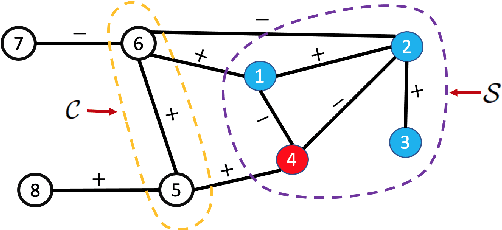
Abstract:3D point cloud (PC) -- a collection of discrete geometric samples of a physical object's surface -- is typically large in size, which entails expensive subsequent operations like viewpoint image rendering and object recognition. Leveraging on recent advances in graph sampling, we propose a fast PC sub-sampling algorithm that reduces its size while preserving the overall object shape. Specifically, to articulate a sampling objective, we first assume a super-resolution (SR) method based on feature graph Laplacian regularization (FGLR) that reconstructs the original high-resolution PC, given 3D points chosen by a sampling matrix $\H$. We prove that minimizing a worst-case SR reconstruction error is equivalent to maximizing the smallest eigenvalue $\lambda_{\min}$ of a matrix $\H^{\top} \H + \mu \cL$, where $\cL$ is a symmetric, positive semi-definite matrix computed from the neighborhood graph connecting the 3D points. Instead, for fast computation we maximize a lower bound $\lambda^-_{\min}(\H^{\top} \H + \mu \cL)$ via selection of $\H$ in three steps. Interpreting $\cL$ as a generalized graph Laplacian matrix corresponding to an unbalanced signed graph $\cG$, we first approximate $\cG$ with a balanced graph $\cG_B$ with the corresponding generalized graph Laplacian matrix $\cL_B$. Second, leveraging on a recent theorem called Gershgorin disc perfect alignment (GDPA), we perform a similarity transform $\cL_p = \S \cL_B \S^{-1}$ so that Gershgorin disc left-ends of $\cL_p$ are all aligned at the same value $\lambda_{\min}(\cL_B)$. Finally, we perform PC sub-sampling on $\cG_B$ using a graph sampling algorithm to maximize $\lambda^-_{\min}(\H^{\top} \H + \mu \cL_p)$ in roughly linear time. Experimental results show that 3D points chosen by our algorithm outperformed competing schemes both numerically and visually in SR reconstruction quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge