Point Cloud Sampling via Graph Balancing and Gershgorin Disc Alignment
Paper and Code
Mar 10, 2021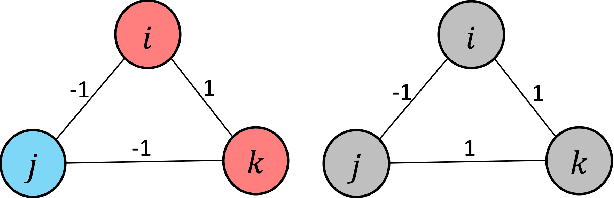
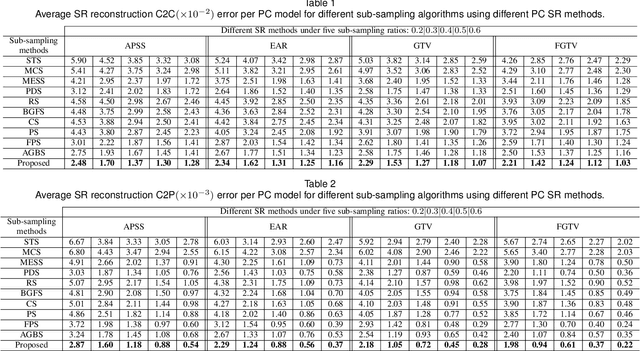
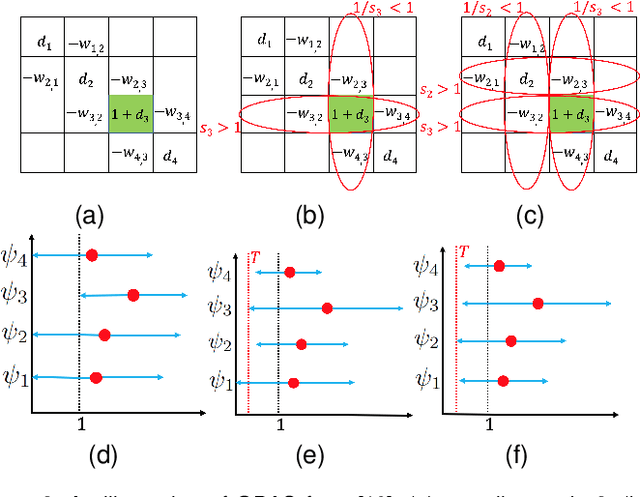
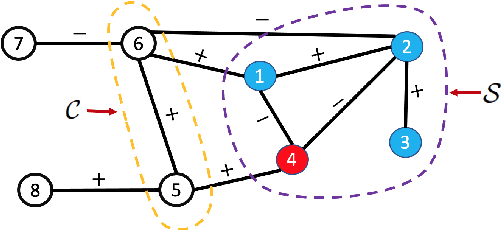
3D point cloud (PC) -- a collection of discrete geometric samples of a physical object's surface -- is typically large in size, which entails expensive subsequent operations like viewpoint image rendering and object recognition. Leveraging on recent advances in graph sampling, we propose a fast PC sub-sampling algorithm that reduces its size while preserving the overall object shape. Specifically, to articulate a sampling objective, we first assume a super-resolution (SR) method based on feature graph Laplacian regularization (FGLR) that reconstructs the original high-resolution PC, given 3D points chosen by a sampling matrix $\H$. We prove that minimizing a worst-case SR reconstruction error is equivalent to maximizing the smallest eigenvalue $\lambda_{\min}$ of a matrix $\H^{\top} \H + \mu \cL$, where $\cL$ is a symmetric, positive semi-definite matrix computed from the neighborhood graph connecting the 3D points. Instead, for fast computation we maximize a lower bound $\lambda^-_{\min}(\H^{\top} \H + \mu \cL)$ via selection of $\H$ in three steps. Interpreting $\cL$ as a generalized graph Laplacian matrix corresponding to an unbalanced signed graph $\cG$, we first approximate $\cG$ with a balanced graph $\cG_B$ with the corresponding generalized graph Laplacian matrix $\cL_B$. Second, leveraging on a recent theorem called Gershgorin disc perfect alignment (GDPA), we perform a similarity transform $\cL_p = \S \cL_B \S^{-1}$ so that Gershgorin disc left-ends of $\cL_p$ are all aligned at the same value $\lambda_{\min}(\cL_B)$. Finally, we perform PC sub-sampling on $\cG_B$ using a graph sampling algorithm to maximize $\lambda^-_{\min}(\H^{\top} \H + \mu \cL_p)$ in roughly linear time. Experimental results show that 3D points chosen by our algorithm outperformed competing schemes both numerically and visually in SR reconstruction quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge