Interaction as Intelligence Part II: Asynchronous Human-Agent Rollout for Long-Horizon Task Training

Large Language Model (LLM) agents have recently shown strong potential in domains such as automated coding, deep research, and graphical user interface manipulation. However, training them to succeed on long-horizon, domain-specialized tasks remains challenging. Current methods primarily fall into two categories. The first relies on dense human annotations through behavior cloning, which is prohibitively expensive for long-horizon tasks that can take days or months. The second depends on outcome-driven sampling, which often collapses due to the rarity of valid positive trajectories on domain-specialized tasks. We introduce Apollo, a sampling framework that integrates asynchronous human guidance with action-level data filtering. Instead of requiring annotators to shadow every step, Apollo allows them to intervene only when the agent drifts from a promising trajectory, by providing prior knowledge, strategic advice, etc. This lightweight design makes it possible to sustain interactions for over 30 hours and produces valuable trajectories at a lower cost. Apollo then applies supervision control to filter out sub-optimal actions and prevent error propagation. Together, these components enable reliable and effective data collection in long-horizon environments. To demonstrate the effectiveness of Apollo, we evaluate it using InnovatorBench. Our experiments show that when applied to train the GLM-4.5 model on InnovatorBench, Apollo achieves more than a 50% improvement over the untrained baseline and a 28% improvement over a variant trained without human interaction. These results highlight the critical role of human-in-the-loop sampling and the robustness of Apollo's design in handling long-horizon, domain-specialized tasks.

Context Engineering 2.0: The Context of Context Engineering

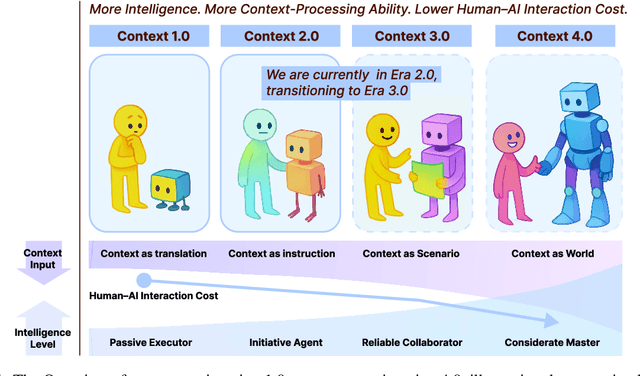
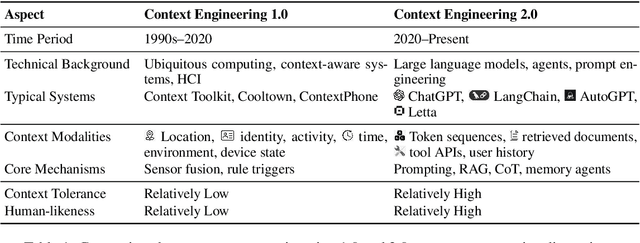
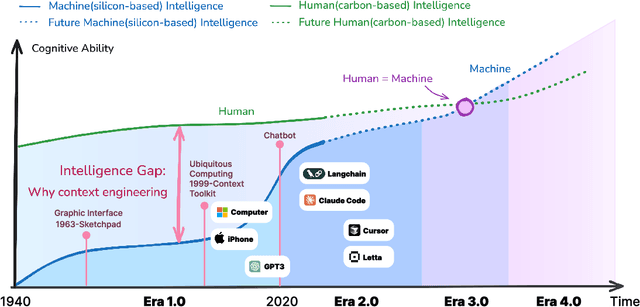
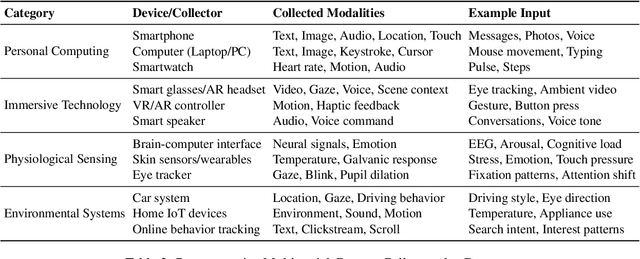
Karl Marx once wrote that ``the human essence is the ensemble of social relations'', suggesting that individuals are not isolated entities but are fundamentally shaped by their interactions with other entities, within which contexts play a constitutive and essential role. With the advent of computers and artificial intelligence, these contexts are no longer limited to purely human--human interactions: human--machine interactions are included as well. Then a central question emerges: How can machines better understand our situations and purposes? To address this challenge, researchers have recently introduced the concept of context engineering. Although it is often regarded as a recent innovation of the agent era, we argue that related practices can be traced back more than twenty years. Since the early 1990s, the field has evolved through distinct historical phases, each shaped by the intelligence level of machines: from early human--computer interaction frameworks built around primitive computers, to today's human--agent interaction paradigms driven by intelligent agents, and potentially to human--level or superhuman intelligence in the future. In this paper, we situate context engineering, provide a systematic definition, outline its historical and conceptual landscape, and examine key design considerations for practice. By addressing these questions, we aim to offer a conceptual foundation for context engineering and sketch its promising future. This paper is a stepping stone for a broader community effort toward systematic context engineering in AI systems.

Synthetic Power Flow Data Generation Using Physics-Informed Denoising Diffusion Probabilistic Models

Many data-driven modules in smart grid rely on access to high-quality power flow data; however, real-world data are often limited due to privacy and operational constraints. This paper presents a physics-informed generative framework based on Denoising Diffusion Probabilistic Models (DDPMs) for synthesizing feasible power flow data. By incorporating auxiliary training and physics-informed loss functions, the proposed method ensures that the generated data exhibit both statistical fidelity and adherence to power system feasibility. We evaluate the approach on the IEEE 14-bus and 30-bus benchmark systems, demonstrating its ability to capture key distributional properties and generalize to out-of-distribution scenarios. Comparative results show that the proposed model outperforms three baseline models in terms of feasibility, diversity, and accuracy of statistical features. This work highlights the potential of integrating generative modelling into data-driven power system applications.

A Trustworthy AIoT-enabled Localization System via Federated Learning and Blockchain

There is a significant demand for indoor localization technology in smart buildings, and the most promising solution in this field is using RF sensors and fingerprinting-based methods that employ machine learning models trained on crowd-sourced user data gathered from IoT devices. However, this raises security and privacy issues in practice. Some researchers propose to use federated learning to partially overcome privacy problems, but there still remain security concerns, e.g., single-point failure and malicious attacks. In this paper, we propose a framework named DFLoc to achieve precise 3D localization tasks while considering the following two security concerns. Particularly, we design a specialized blockchain to decentralize the framework by distributing the tasks such as model distribution and aggregation which are handled by a central server to all clients in most previous works, to address the issue of the single-point failure for a reliable and accurate indoor localization system. Moreover, we introduce an updated model verification mechanism within the blockchain to alleviate the concern of malicious node attacks. Experimental results substantiate the framework's capacity to deliver accurate 3D location predictions and its superior resistance to the impacts of single-point failure and malicious attacks when compared to conventional centralized federated learning systems.

Complex Graph Laplacian Regularizer for Inferencing Grid States

In order to maintain stable grid operations, system monitoring and control processes require the computation of grid states (e.g. voltage magnitude and angles) at high granularity. It is necessary to infer these grid states from measurements generated by a limited number of sensors like phasor measurement units (PMUs) that can be subjected to delays and losses due to channel artefacts, and/or adversarial attacks (e.g. denial of service, jamming, etc.). We propose a novel graph signal processing (GSP) based algorithm to interpolate states of the entire grid from observations of a small number of grid measurements. It is a two-stage process, where first an underlying Hermitian graph is learnt empirically from existing grid datasets. Then, the graph is used to interpolate missing grid signal samples in linear time. With our proposal, we can effectively reconstruct grid signals with significantly smaller number of observations when compared to existing traditional approaches (e.g. state estimation). In contrast to existing GSP approaches, we do not require knowledge of the underlying grid structure and parameters and are able to guarantee fast spectral optimization. We demonstrate the computational efficacy and accuracy of our proposal via practical studies conducted on the IEEE 118 bus system.