Learning Sparse Graph Laplacian with $K$ Eigenvector Prior via Iterative GLASSO and Projection
Paper and Code
Oct 25, 2020
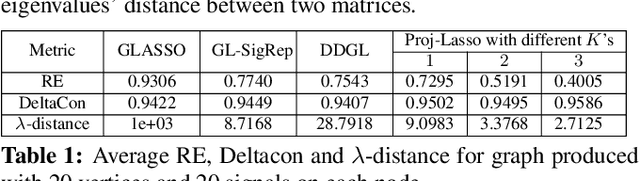
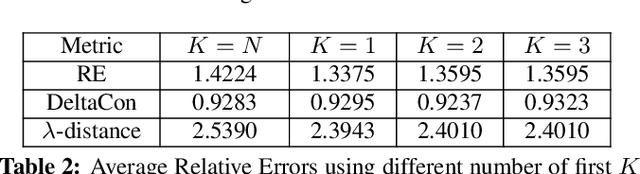
Learning a suitable graph is an important precursor to many graph signal processing (GSP) pipelines, such as graph spectral signal compression and denoising. Previous graph learning algorithms either i) make some assumptions on connectivity (e.g., graph sparsity), or ii) make simple graph edge assumptions such as positive edges only. In this paper, given an empirical covariance matrix $\bar{C}$ computed from data as input, we consider a structural assumption on the graph Laplacian matrix $L$: the first $K$ eigenvectors of $L$ are pre-selected, e.g., based on domain-specific criteria, such as computation requirement, and the remaining eigenvectors are then learned from data. One example use case is image coding, where the first eigenvector is pre-chosen to be constant, regardless of available observed data. We first prove that the subspace of symmetric positive semi-definite (PSD) matrices $H_{u}^+$ with the first $K$ eigenvectors being $\{u_k\}$ in a defined Hilbert space is a convex cone. We then construct an operator to project a given positive definite (PD) matrix $L$ to $H_{u}^+$, inspired by the Gram-Schmidt procedure. Finally, we design an efficient hybrid graphical lasso/projection algorithm to compute the most suitable graph Laplacian matrix $L^* \in H_{u}^+$ given $\bar{C}$. Experimental results show that given the first $K$ eigenvectors as a prior, our algorithm outperforms competing graph learning schemes using a variety of graph comparison metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge