Towards Reproducible Learning-based Compression

A deep learning system typically suffers from a lack of reproducibility that is partially rooted in hardware or software implementation details. The irreproducibility leads to skepticism in deep learning technologies and it can hinder them from being deployed in many applications. In this work, the irreproducibility issue is analyzed where deep learning is employed in compression systems while the encoding and decoding may be run on devices from different manufacturers. The decoding process can even crash due to a single bit difference, e.g., in a learning-based entropy coder. For a given deep learning-based module with limited resources for protection, we first suggest that reproducibility can only be assured when the mismatches are bounded. Then a safeguarding mechanism is proposed to tackle the challenges. The proposed method may be applied for different levels of protection either at the reconstruction level or at a selected decoding level. Furthermore, the overhead introduced for the protection can be scaled down accordingly when the error bound is being suppressed. Experiments demonstrate the effectiveness of the proposed approach for learning-based compression systems, e.g., in image compression and point cloud compression.

PIVOT-Net: Heterogeneous Point-Voxel-Tree-based Framework for Point Cloud Compression

The universality of the point cloud format enables many 3D applications, making the compression of point clouds a critical phase in practice. Sampled as discrete 3D points, a point cloud approximates 2D surface(s) embedded in 3D with a finite bit-depth. However, the point distribution of a practical point cloud changes drastically as its bit-depth increases, requiring different methodologies for effective consumption/analysis. In this regard, a heterogeneous point cloud compression (PCC) framework is proposed. We unify typical point cloud representations -- point-based, voxel-based, and tree-based representations -- and their associated backbones under a learning-based framework to compress an input point cloud at different bit-depth levels. Having recognized the importance of voxel-domain processing, we augment the framework with a proposed context-aware upsampling for decoding and an enhanced voxel transformer for feature aggregation. Extensive experimentation demonstrates the state-of-the-art performance of our proposal on a wide range of point clouds.

WrappingNet: Mesh Autoencoder via Deep Sphere Deformation

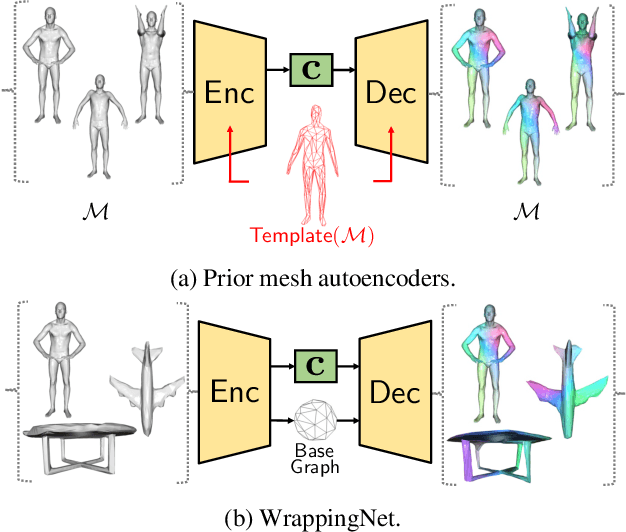
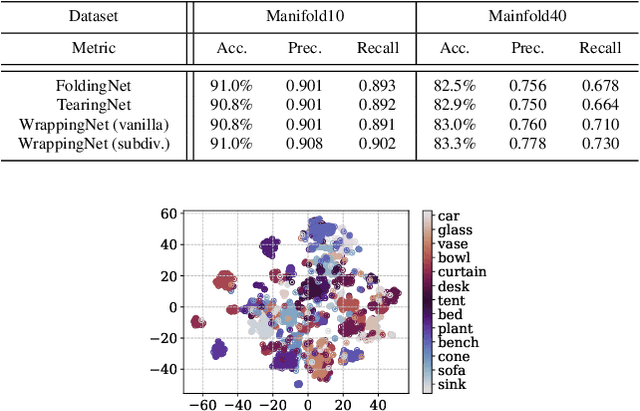
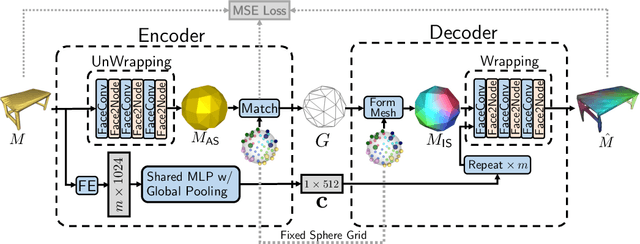
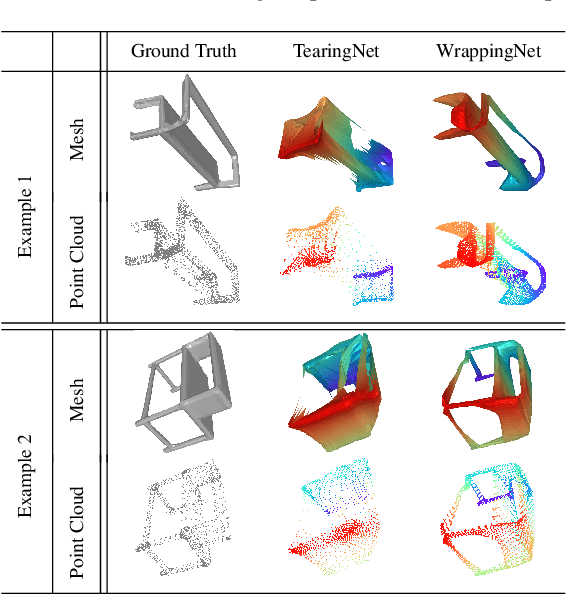
There have been recent efforts to learn more meaningful representations via fixed length codewords from mesh data, since a mesh serves as a complete model of underlying 3D shape compared to a point cloud. However, the mesh connectivity presents new difficulties when constructing a deep learning pipeline for meshes. Previous mesh unsupervised learning approaches typically assume category-specific templates, e.g., human face/body templates. It restricts the learned latent codes to only be meaningful for objects in a specific category, so the learned latent spaces are unable to be used across different types of objects. In this work, we present WrappingNet, the first mesh autoencoder enabling general mesh unsupervised learning over heterogeneous objects. It introduces a novel base graph in the bottleneck dedicated to representing mesh connectivity, which is shown to facilitate learning a shared latent space representing object shape. The superiority of WrappingNet mesh learning is further demonstrated via improved reconstruction quality and competitive classification compared to point cloud learning, as well as latent interpolation between meshes of different categories.

GRASP-Net: Geometric Residual Analysis and Synthesis for Point Cloud Compression

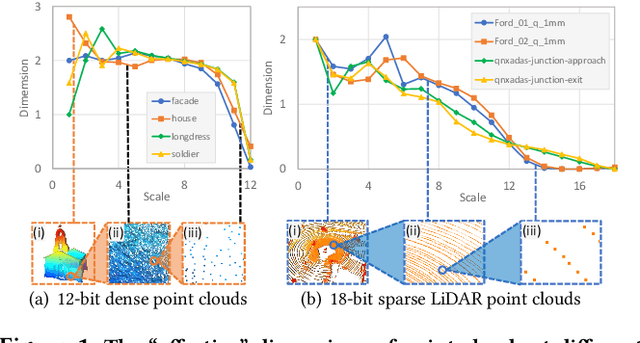
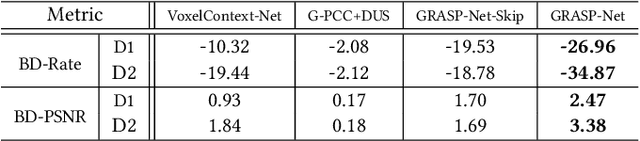
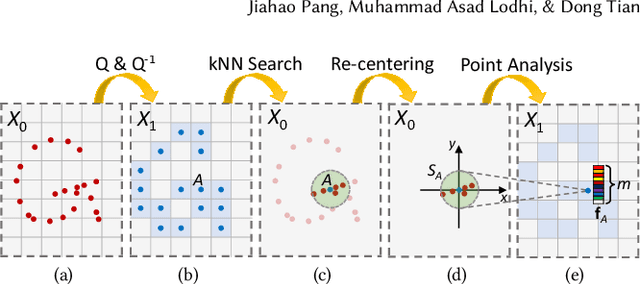
Point cloud compression (PCC) is a key enabler for various 3-D applications, owing to the universality of the point cloud format. Ideally, 3D point clouds endeavor to depict object/scene surfaces that are continuous. Practically, as a set of discrete samples, point clouds are locally disconnected and sparsely distributed. This sparse nature is hindering the discovery of local correlation among points for compression. Motivated by an analysis with fractal dimension, we propose a heterogeneous approach with deep learning for lossy point cloud geometry compression. On top of a base layer compressing a coarse representation of the input, an enhancement layer is designed to cope with the challenging geometric residual/details. Specifically, a point-based network is applied to convert the erratic local details to latent features residing on the coarse point cloud. Then a sparse convolutional neural network operating on the coarse point cloud is launched. It utilizes the continuity/smoothness of the coarse geometry to compress the latent features as an enhancement bit-stream that greatly benefits the reconstruction quality. When this bit-stream is unavailable, e.g., due to packet loss, we support a skip mode with the same architecture which generates geometric details from the coarse point cloud directly. Experimentation on both dense and sparse point clouds demonstrate the state-of-the-art compression performance achieved by our proposal. Our code is available at https://github.com/InterDigitalInc/GRASP-Net.

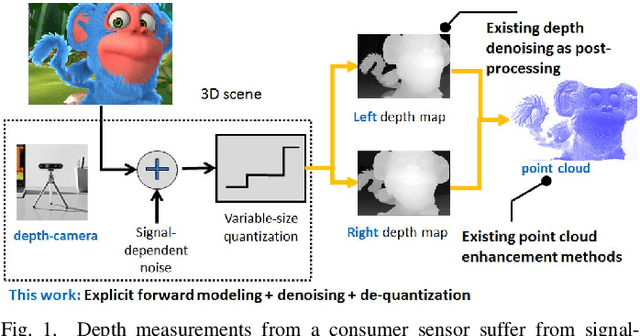
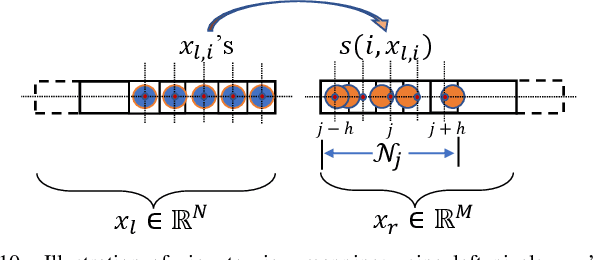
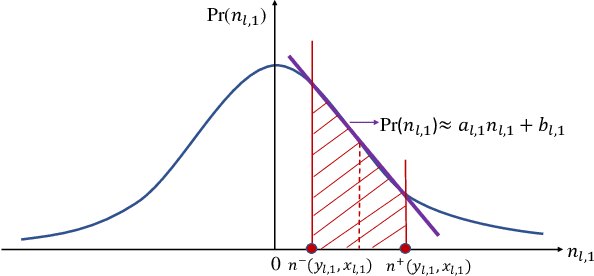
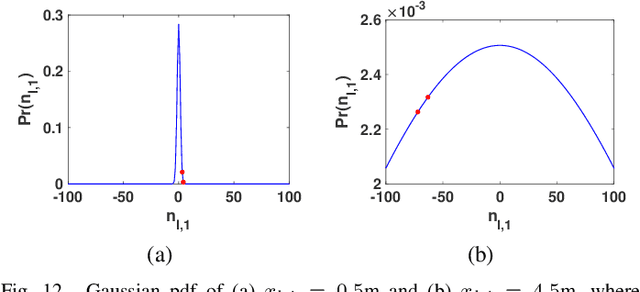
Graph-Based Depth Denoising & Dequantization for Point Cloud Enhancement

A 3D point cloud is typically constructed from depth measurements acquired by sensors at one or more viewpoints. The measurements suffer from both quantization and noise corruption. To improve quality, previous works denoise a point cloud \textit{a posteriori} after projecting the imperfect depth data onto 3D space. Instead, we enhance depth measurements directly on the sensed images \textit{a priori}, before synthesizing a 3D point cloud. By enhancing near the physical sensing process, we tailor our optimization to our depth formation model before subsequent processing steps that obscure measurement errors. Specifically, we model depth formation as a combined process of signal-dependent noise addition and non-uniform log-based quantization. The designed model is validated (with parameters fitted) using collected empirical data from an actual depth sensor. To enhance each pixel row in a depth image, we first encode intra-view similarities between available row pixels as edge weights via feature graph learning. We next establish inter-view similarities with another rectified depth image via viewpoint mapping and sparse linear interpolation. This leads to a maximum a posteriori (MAP) graph filtering objective that is convex and differentiable. We optimize the objective efficiently using accelerated gradient descent (AGD), where the optimal step size is approximated via Gershgorin circle theorem (GCT). Experiments show that our method significantly outperformed recent point cloud denoising schemes and state-of-the-art image denoising schemes, in two established point cloud quality metrics.

FESTA: Flow Estimation via Spatial-Temporal Attention for Scene Point Clouds

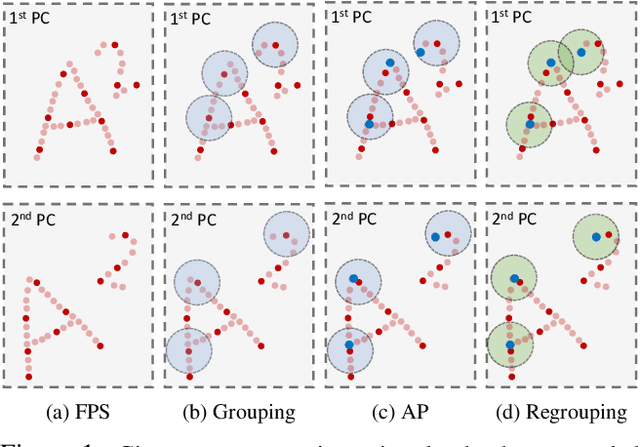
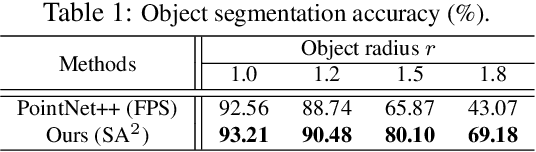
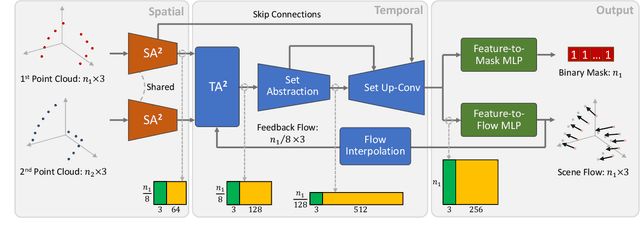
Scene flow depicts the dynamics of a 3D scene, which is critical for various applications such as autonomous driving, robot navigation, AR/VR, etc. Conventionally, scene flow is estimated from dense/regular RGB video frames. With the development of depth-sensing technologies, precise 3D measurements are available via point clouds which have sparked new research in 3D scene flow. Nevertheless, it remains challenging to extract scene flow from point clouds due to the sparsity and irregularity in typical point cloud sampling patterns. One major issue related to irregular sampling is identified as the randomness during point set abstraction/feature extraction -- an elementary process in many flow estimation scenarios. A novel Spatial Abstraction with Attention (SA^2) layer is accordingly proposed to alleviate the unstable abstraction problem. Moreover, a Temporal Abstraction with Attention (TA^2) layer is proposed to rectify attention in temporal domain, leading to benefits with motions scaled in a larger range. Extensive analysis and experiments verified the motivation and significant performance gains of our method, dubbed as Flow Estimation via Spatial-Temporal Attention (FESTA), when compared to several state-of-the-art benchmarks of scene flow estimation.

Graph Signal Processing for Geometric Data and Beyond: Theory and Applications

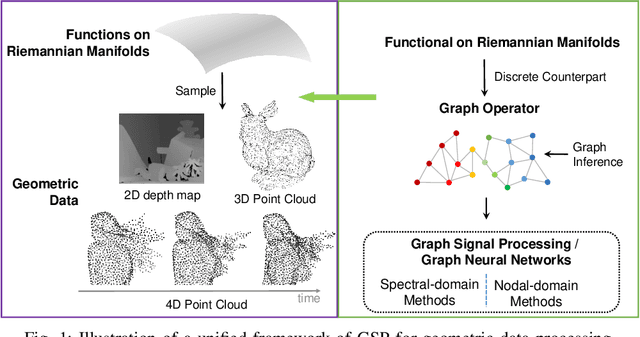
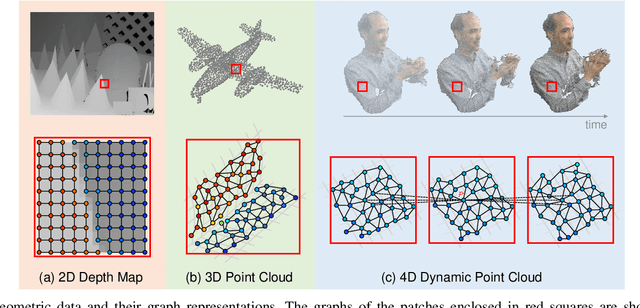
Geometric data acquired from real-world scenes, e.g., 2D depth images, 3D point clouds, and 4D dynamic point clouds, have found a wide range of applications including immersive telepresence, autonomous driving, surveillance, etc. Due to irregular sampling patterns of most geometric data, traditional image/video processing methodologies are limited, while Graph Signal Processing (GSP)---a fast-developing field in the signal processing community---enables processing signals that reside on irregular domains and plays a critical role in numerous applications of geometric data from low-level processing to high-level analysis. To further advance the research in this field, we provide the first timely and comprehensive overview of GSP methodologies for geometric data in a unified manner by bridging the connections between geometric data and graphs, among the various geometric data modalities, and with spectral/nodal graph filtering techniques. We also discuss the recently developed Graph Neural Networks (GNNs) and interpret the operation of these networks from the perspective of GSP. We conclude with a brief discussion of open problems and challenges.

TearingNet: Point Cloud Autoencoder to Learn Topology-Friendly Representations

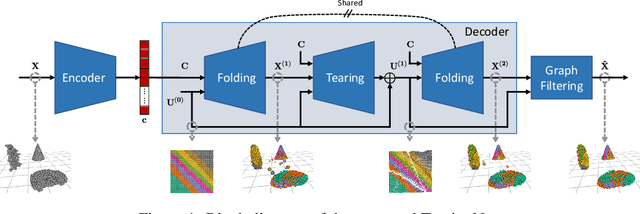
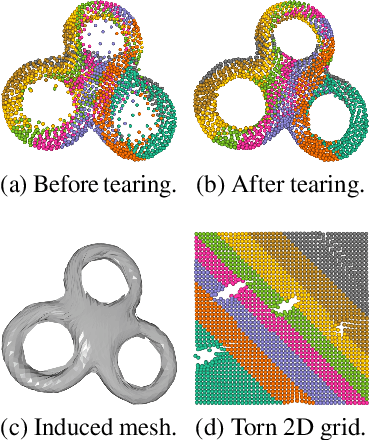
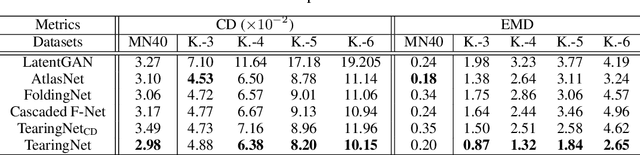
Topology matters. Despite the recent success of point cloud processing with geometric deep learning, it remains arduous to capture the complex topologies of point cloud data with a learning model. Given a point cloud dataset containing objects with various genera or scenes with multiple objects, we propose an autoencoder, TearingNet, which tackles the challenging task of representing the point clouds using a fixed-length descriptor. Unlike existing works to deform primitives of genus zero (e.g., a 2D square patch) to an object-level point cloud, we propose a function which tears the primitive during deformation, letting it emulate the topology of a target point cloud. From the torn primitive, we construct a locally-connected graph to further enforce the learned topology via filtering. Moreover, we analyze a widely existing problem which we call point-collapse when processing point clouds with diverse topologies. Correspondingly, we propose a subtractive sculpture strategy to train our TearingNet model. Experimentation finally shows the superiority of our proposal in terms of reconstructing more faithful point clouds as well as generating more topology-friendly representations than benchmarks.

Deep End-to-End Alignment and Refinement for Time-of-Flight RGB-D Module

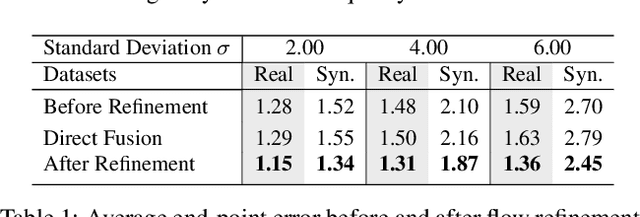
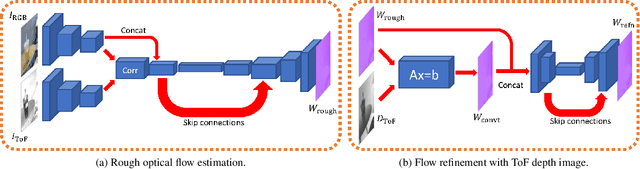
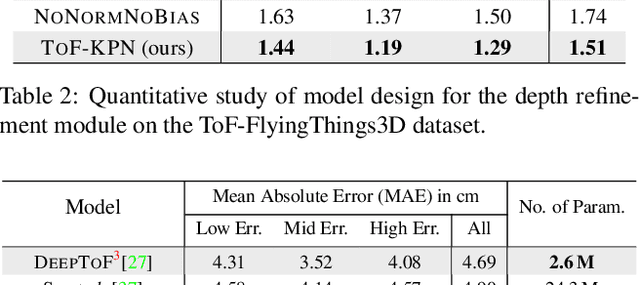
Recently, it is increasingly popular to equip mobile RGB cameras with Time-of-Flight (ToF) sensors for active depth sensing. However, for off-the-shelf ToF sensors, one must tackle two problems in order to obtain high-quality depth with respect to the RGB camera, namely 1) online calibration and alignment; and 2) complicated error correction for ToF depth sensing. In this work, we propose a framework for jointly alignment and refinement via deep learning. First, a cross-modal optical flow between the RGB image and the ToF amplitude image is estimated for alignment. The aligned depth is then refined via an improved kernel predicting network that performs kernel normalization and applies the bias prior to the dynamic convolution. To enrich our data for end-to-end training, we have also synthesized a dataset using tools from computer graphics. Experimental results demonstrate the effectiveness of our approach, achieving state-of-the-art for ToF refinement.

DSR: Direct Self-rectification for Uncalibrated Dual-lens Cameras

With the developments of dual-lens camera modules,depth information representing the third dimension of thecaptured scenes becomes available for smartphones. It isestimated by stereo matching algorithms, taking as input thetwo views captured by dual-lens cameras at slightly differ-ent viewpoints. Depth-of-field rendering (also be referred toas synthetic defocus or bokeh) is one of the trending depth-based applications. However, to achieve fast depth estima-tion on smartphones, the stereo pairs need to be rectified inthe first place. In this paper, we propose a cost-effective so-lution to perform stereo rectification for dual-lens camerascalled direct self-rectification, short for DSR1. It removesthe need of individual offline calibration for every pair ofdual-lens cameras. In addition, the proposed solution isrobust to the slight movements, e.g., due to collisions, ofthe dual-lens cameras after fabrication. Different with ex-isting self-rectification approaches, our approach computesthe homography in a novel way with zero geometric distor-tions introduced to the master image. It is achieved by di-rectly minimizing the vertical displacements of correspond-ing points between the original master image and the trans-formed slave image. Our method is evaluated on both real-istic and synthetic stereo image pairs, and produces supe-rior results compared to the calibrated rectification or otherself-rectification approaches