Towards equilibrium molecular conformation generation with GFlowNets

Sampling diverse, thermodynamically feasible molecular conformations plays a crucial role in predicting properties of a molecule. In this paper we propose to use GFlowNet for sampling conformations of small molecules from the Boltzmann distribution, as determined by the molecule's energy. The proposed approach can be used in combination with energy estimation methods of different fidelity and discovers a diverse set of low-energy conformations for highly flexible drug-like molecules. We demonstrate that GFlowNet can reproduce molecular potential energy surfaces by sampling proportionally to the Boltzmann distribution.

Crystal-GFN: sampling crystals with desirable properties and constraints

Accelerating material discovery holds the potential to greatly help mitigate the climate crisis. Discovering new solid-state crystals such as electrocatalysts, ionic conductors or photovoltaics can have a crucial impact, for instance, in improving the efficiency of renewable energy production and storage. In this paper, we introduce Crystal-GFlowNet, a generative model of crystal structures that sequentially samples a crystal's composition, space group and lattice parameters. This domain-inspired approach enables the flexible incorporation of physical and geometrical constraints, as well as the use of any available predictive model of a desired property as an objective function. We evaluate the capabilities of Crystal-GFlowNet by using as objective the formation energy of a crystal structure, as predicted by a new proxy model trained on MatBench. The results demonstrate that Crystal-GFlowNet is able to sample diverse crystals with low formation energy.

A theory of continuous generative flow networks

Generative flow networks (GFlowNets) are amortized variational inference algorithms that are trained to sample from unnormalized target distributions over compositional objects. A key limitation of GFlowNets until this time has been that they are restricted to discrete spaces. We present a theory for generalized GFlowNets, which encompasses both existing discrete GFlowNets and ones with continuous or hybrid state spaces, and perform experiments with two goals in mind. First, we illustrate critical points of the theory and the importance of various assumptions. Second, we empirically demonstrate how observations about discrete GFlowNets transfer to the continuous case and show strong results compared to non-GFlowNet baselines on several previously studied tasks. This work greatly widens the perspectives for the application of GFlowNets in probabilistic inference and various modeling settings.

Generative Flow Networks for Discrete Probabilistic Modeling

We present energy-based generative flow networks (EB-GFN), a novel probabilistic modeling algorithm for high-dimensional discrete data. Building upon the theory of generative flow networks (GFlowNets), we model the generation process by a stochastic data construction policy and thus amortize expensive MCMC exploration into a fixed number of actions sampled from a GFlowNet. We show how GFlowNets can approximately perform large-block Gibbs sampling to mix between modes. We propose a framework to jointly train a GFlowNet with an energy function, so that the GFlowNet learns to sample from the energy distribution, while the energy learns with an approximate MLE objective with negative samples from the GFlowNet. We demonstrate EB-GFN's effectiveness on various probabilistic modeling tasks.

Stochasticity in Neural ODEs: An Empirical Study

Stochastic regularization of neural networks (e.g. dropout) is a wide-spread technique in deep learning that allows for better generalization. Despite its success, continuous-time models, such as neural ordinary differential equation (ODE), usually rely on a completely deterministic feed-forward operation. This work provides an empirical study of stochastically regularized neural ODE on several image-classification tasks (CIFAR-10, CIFAR-100, TinyImageNet). Building upon the formalism of stochastic differential equations (SDEs), we demonstrate that neural SDE is able to outperform its deterministic counterpart. Further, we show that data augmentation during the training improves the performance of both deterministic and stochastic versions of the same model. However, the improvements obtained by the data augmentation completely eliminate the empirical gains of the stochastic regularization, making the difference in the performance of neural ODE and neural SDE negligible.

Semi-Conditional Normalizing Flows for Semi-Supervised Learning

This paper proposes a semi-conditional normalizing flow model for semi-supervised learning. The model uses both labelled and unlabeled data to learn an explicit model of joint distribution over objects and labels. Semi-conditional architecture of the model allows us to efficiently compute a value and gradients of the marginal likelihood for unlabeled objects. The conditional part of the model is based on a proposed conditional coupling layer. We demonstrate performance of the model for semi-supervised classification problem on different datasets. The model outperforms the baseline approach based on variational auto-encoders on MNIST dataset.

Cherenkov Detectors Fast Simulation Using Neural Networks

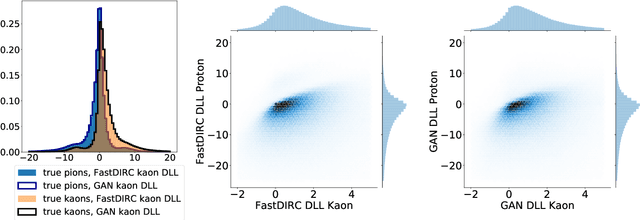
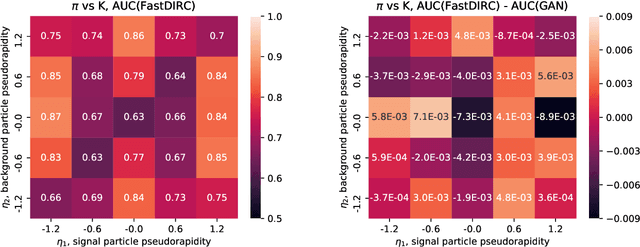
We propose a way to simulate Cherenkov detector response using a generative adversarial neural network to bypass low-level details. This network is trained to reproduce high level features of the simulated detector events based on input observables of incident particles. This allows the dramatic increase of simulation speed. We demonstrate that this approach provides simulation precision which is consistent with the baseline and discuss possible implications of these results.