How to do impactful research in artificial intelligence for chemistry and materials science

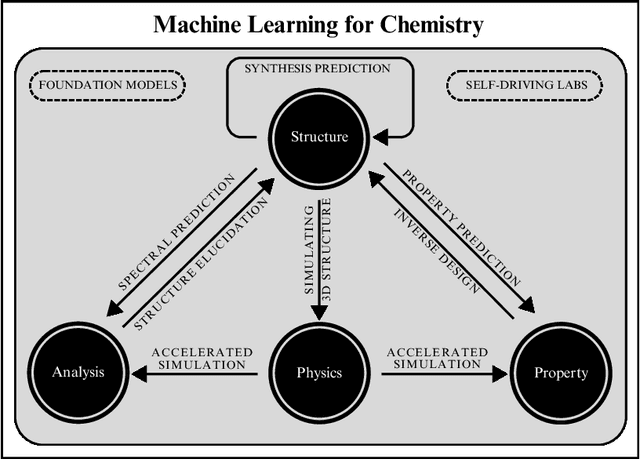
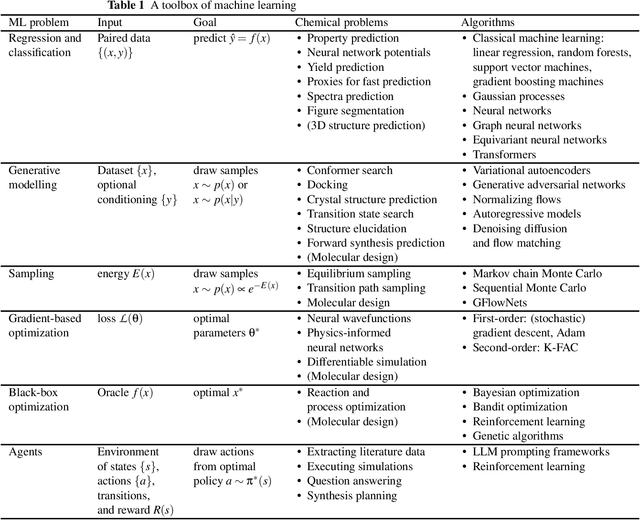
Machine learning has been pervasively touching many fields of science. Chemistry and materials science are no exception. While machine learning has been making a great impact, it is still not reaching its full potential or maturity. In this perspective, we first outline current applications across a diversity of problems in chemistry. Then, we discuss how machine learning researchers view and approach problems in the field. Finally, we provide our considerations for maximizing impact when researching machine learning for chemistry.

Sorting Out Quantum Monte Carlo

Molecular modeling at the quantum level requires choosing a parameterization of the wavefunction that both respects the required particle symmetries, and is scalable to systems of many particles. For the simulation of fermions, valid parameterizations must be antisymmetric with respect to the exchange of particles. Typically, antisymmetry is enforced by leveraging the anti-symmetry of determinants with respect to the exchange of matrix rows, but this involves computing a full determinant each time the wavefunction is evaluated. Instead, we introduce a new antisymmetrization layer derived from sorting, the $\textit{sortlet}$, which scales as $O(N \log N)$ with regards to the number of particles -- in contrast to $O(N^3)$ for the determinant. We show numerically that applying this anti-symmeterization layer on top of an attention based neural-network backbone yields a flexible wavefunction parameterization capable of reaching chemical accuracy when approximating the ground state of first-row atoms and small molecules.

Towards equilibrium molecular conformation generation with GFlowNets

Sampling diverse, thermodynamically feasible molecular conformations plays a crucial role in predicting properties of a molecule. In this paper we propose to use GFlowNet for sampling conformations of small molecules from the Boltzmann distribution, as determined by the molecule's energy. The proposed approach can be used in combination with energy estimation methods of different fidelity and discovers a diverse set of low-energy conformations for highly flexible drug-like molecules. We demonstrate that GFlowNet can reproduce molecular potential energy surfaces by sampling proportionally to the Boltzmann distribution.

Wasserstein Quantum Monte Carlo: A Novel Approach for Solving the Quantum Many-Body Schrödinger Equation

Solving the quantum many-body Schr\"odinger equation is a fundamental and challenging problem in the fields of quantum physics, quantum chemistry, and material sciences. One of the common computational approaches to this problem is Quantum Variational Monte Carlo (QVMC), in which ground-state solutions are obtained by minimizing the energy of the system within a restricted family of parameterized wave functions. Deep learning methods partially address the limitations of traditional QVMC by representing a rich family of wave functions in terms of neural networks. However, the optimization objective in QVMC remains notoriously hard to minimize and requires second-order optimization methods such as natural gradient. In this paper, we first reformulate energy functional minimization in the space of Born distributions corresponding to particle-permutation (anti-)symmetric wave functions, rather than the space of wave functions. We then interpret QVMC as the Fisher-Rao gradient flow in this distributional space, followed by a projection step onto the variational manifold. This perspective provides us with a principled framework to derive new QMC algorithms, by endowing the distributional space with better metrics, and following the projected gradient flow induced by those metrics. More specifically, we propose "Wasserstein Quantum Monte Carlo" (WQMC), which uses the gradient flow induced by the Wasserstein metric, rather than Fisher-Rao metric, and corresponds to transporting the probability mass, rather than teleporting it. We demonstrate empirically that the dynamics of WQMC results in faster convergence to the ground state of molecular systems.

Waveflow: Enforcing boundary conditions in smooth normalizing flows with application to fermionic wave functions

In this paper, we introduce four main novelties: First, we present a new way of handling the topology problem of normalizing flows. Second, we describe a technique to enforce certain classes of boundary conditions onto normalizing flows. Third, we introduce the I-Spline bijection, which, similar to previous work, leverages splines but, in contrast to those works, can be made arbitrarily often differentiable. And finally, we use these techniques to create Waveflow, an Ansatz for the one-space-dimensional multi-particle fermionic wave functions in real space based on normalizing flows, that can be efficiently trained with Variational Quantum Monte Carlo without the need for MCMC nor estimation of a normalization constant. To enforce the necessary anti-symmetry of fermionic wave functions, we train the normalizing flow only on the fundamental domain of the permutation group, which effectively reduces it to a boundary value problem.