Jack Richter-Powell
Sorting Out Quantum Monte Carlo
Nov 09, 2023Abstract:Molecular modeling at the quantum level requires choosing a parameterization of the wavefunction that both respects the required particle symmetries, and is scalable to systems of many particles. For the simulation of fermions, valid parameterizations must be antisymmetric with respect to the exchange of particles. Typically, antisymmetry is enforced by leveraging the anti-symmetry of determinants with respect to the exchange of matrix rows, but this involves computing a full determinant each time the wavefunction is evaluated. Instead, we introduce a new antisymmetrization layer derived from sorting, the $\textit{sortlet}$, which scales as $O(N \log N)$ with regards to the number of particles -- in contrast to $O(N^3)$ for the determinant. We show numerically that applying this anti-symmeterization layer on top of an attention based neural-network backbone yields a flexible wavefunction parameterization capable of reaching chemical accuracy when approximating the ground state of first-row atoms and small molecules.
Neural Conservation Laws: A Divergence-Free Perspective
Oct 04, 2022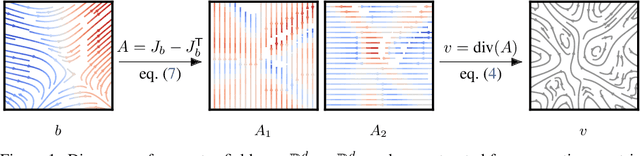
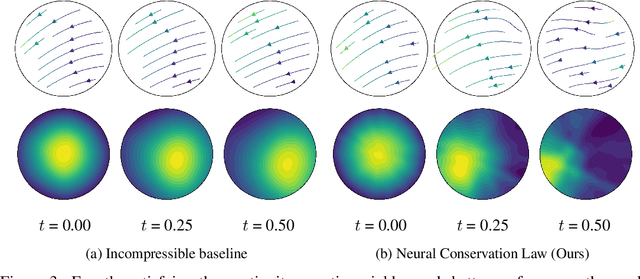
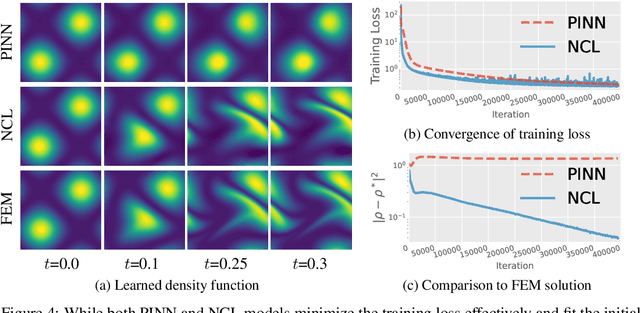
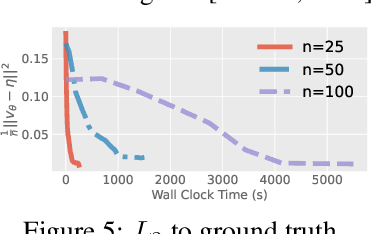
Abstract:We investigate the parameterization of deep neural networks that by design satisfy the continuity equation, a fundamental conservation law. This is enabled by the observation that solutions of the continuity equation can be represented as a divergence-free vector field. We hence propose building divergence-free neural networks through the concept of differential forms, and with the aid of automatic differentiation, realize two practical constructions. As a result, we can parameterize pairs of densities and vector fields that always satisfy the continuity equation by construction, foregoing the need for extra penalty methods or expensive numerical simulation. Furthermore, we prove these models are universal and so can be used to represent any divergence-free vector field. Finally, we experimentally validate our approaches on neural network-based solutions to fluid equations, solving for the Hodge decomposition, and learning dynamical optimal transport maps the Hodge decomposition, and learning dynamical optimal transport maps.
Input Convex Gradient Networks
Nov 23, 2021
Abstract:The gradients of convex functions are expressive models of non-trivial vector fields. For example, Brenier's theorem yields that the optimal transport map between any two measures on Euclidean space under the squared distance is realized as a convex gradient, which is a key insight used in recent generative flow models. In this paper, we study how to model convex gradients by integrating a Jacobian-vector product parameterized by a neural network, which we call the Input Convex Gradient Network (ICGN). We theoretically study ICGNs and compare them to taking the gradient of an Input-Convex Neural Network (ICNN), empirically demonstrating that a single layer ICGN can fit a toy example better than a single layer ICNN. Lastly, we explore extensions to deeper networks and connections to constructions from Riemannian geometry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge