Transition1x -- a Dataset for Building Generalizable Reactive Machine Learning Potentials

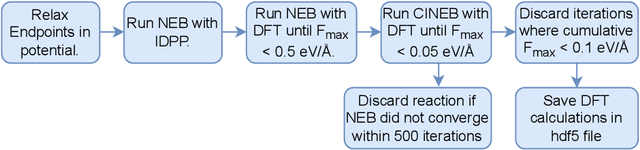
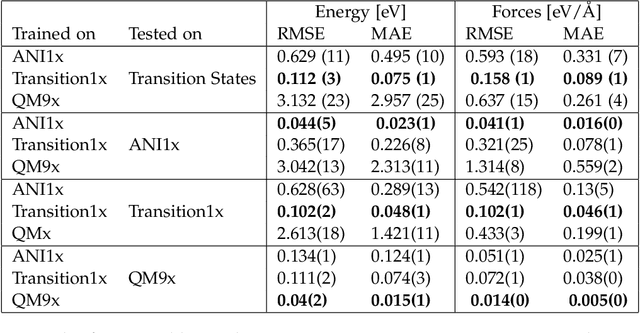
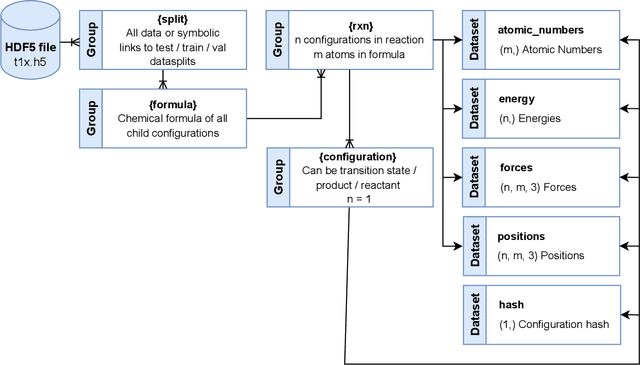
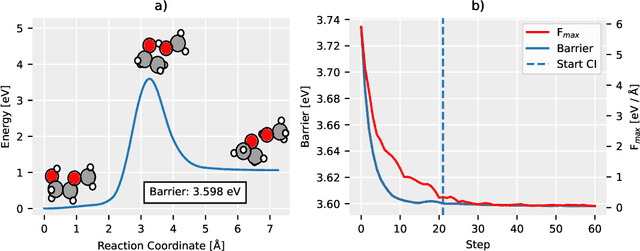
Machine Learning (ML) models have, in contrast to their usefulness in molecular dynamics studies, had limited success as surrogate potentials for reaction barrier search. It is due to the scarcity of training data in relevant transition state regions of chemical space. Currently, available datasets for training ML models on small molecular systems almost exclusively contain configurations at or near equilibrium. In this work, we present the dataset Transition1x containing 9.6 million Density Functional Theory (DFT) calculations of forces and energies of molecular configurations on and around reaction pathways at the wB97x/6-31G(d) level of theory. The data was generated by running Nudged Elastic Band (NEB) calculations with DFT on 10k reactions while saving intermediate calculations. We train state-of-the-art equivariant graph message-passing neural network models on Transition1x and cross-validate on the popular ANI1x and QM9 datasets. We show that ML models cannot learn features in transition-state regions solely by training on hitherto popular benchmark datasets. Transition1x is a new challenging benchmark that will provide an important step towards developing next-generation ML force fields that also work far away from equilibrium configurations and reactive systems.

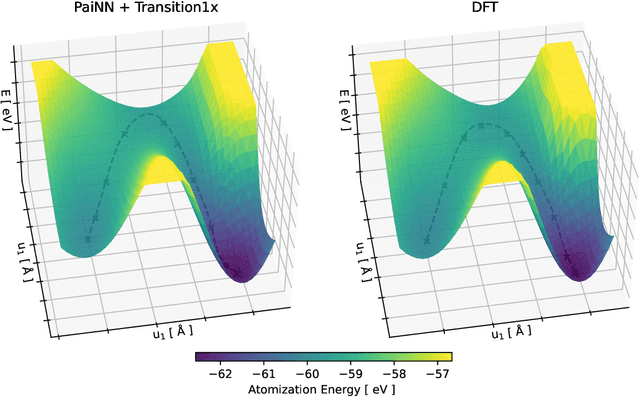
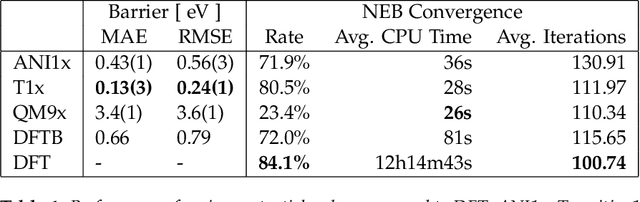
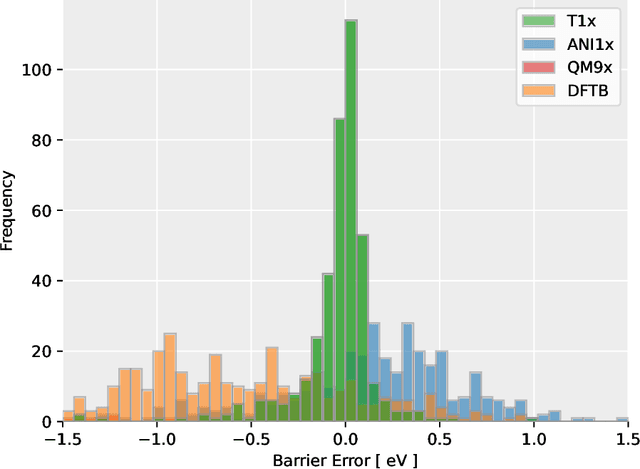
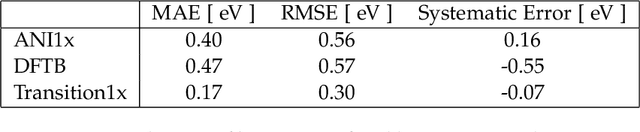
NeuralNEB -- Neural Networks can find Reaction Paths Fast

Quantum mechanical methods like Density Functional Theory (DFT) are used with great success alongside efficient search algorithms for studying kinetics of reactive systems. However, DFT is prohibitively expensive for large scale exploration. Machine Learning (ML) models have turned out to be excellent emulators of small molecule DFT calculations and could possibly replace DFT in such tasks. For kinetics, success relies primarily on the models capability to accurately predict the Potential Energy Surface (PES) around transition-states and Minimal Energy Paths (MEPs). Previously this has not been possible due to scarcity of relevant data in the literature. In this paper we train state of the art equivariant Graph Neural Network (GNN)-based models on around 10.000 elementary reactions from the Transition1x dataset. We apply the models as potentials for the Nudged Elastic Band (NEB) algorithm and achieve a Mean Average Error (MAE) of 0.13+/-0.03 eV on barrier energies on unseen reactions. We compare the results against equivalent models trained on QM9 and ANI1x. We also compare with and outperform Density Functional based Tight Binding (DFTB) on both accuracy and computational resource. The implication is that ML models, given relevant data, are now at a level where they can be applied for downstream tasks in quantum chemistry transcending prediction of simple molecular features.

Graph neural networks for fast electron density estimation of molecules, liquids, and solids

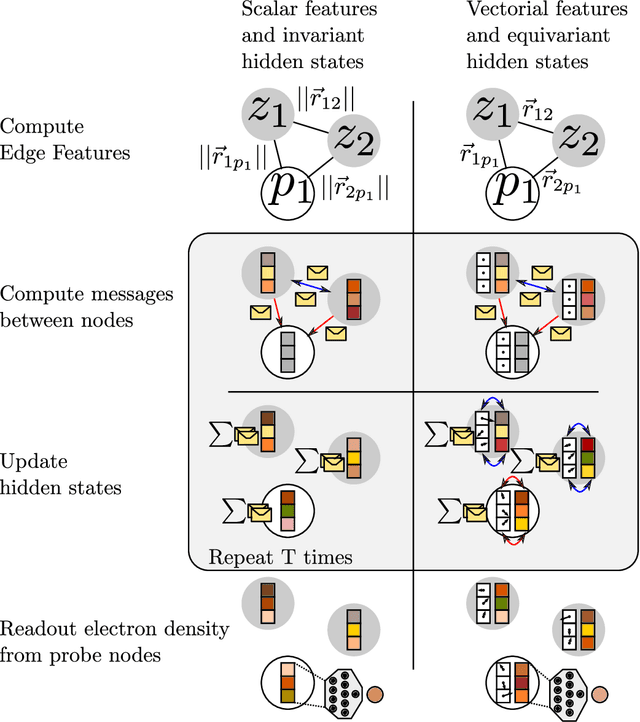
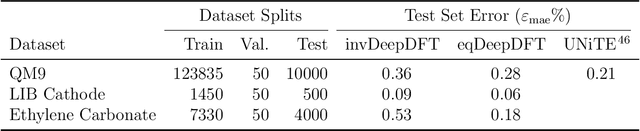
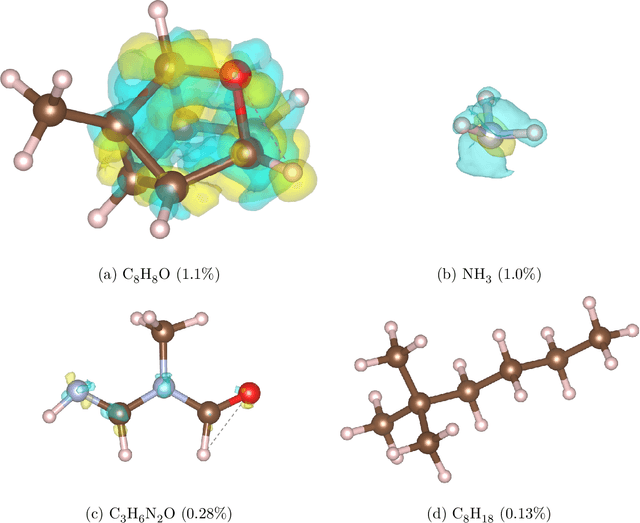
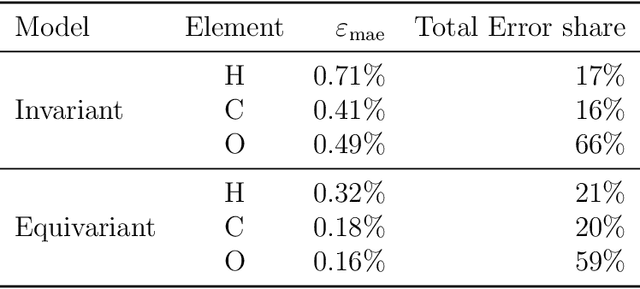
Electron density $\rho(\vec{r})$ is the fundamental variable in the calculation of ground state energy with density functional theory (DFT). Beyond total energy, features in $\rho(\vec{r})$ distribution and modifications in $\rho(\vec{r})$ are often used to capture critical physicochemical phenomena in functional materials and molecules at the electronic scale. Methods providing access to $\rho(\vec{r})$ of complex disordered systems with little computational cost can be a game changer in the expedited exploration of materials phase space towards the inverse design of new materials with better functionalities. We present a machine learning framework for the prediction of $\rho(\vec{r})$. The model is based on equivariant graph neural networks and the electron density is predicted at special query point vertices that are part of the message passing graph, but only receive messages. The model is tested across multiple data sets of molecules (QM9), liquid ethylene carbonate electrolyte (EC) and LixNiyMnzCo(1-y-z)O2 lithium ion battery cathodes (NMC). For QM9 molecules, the accuracy of the proposed model exceeds typical variability in $\rho(\vec{r})$ obtained from DFT done with different exchange-correlation functional and show beyond the state of the art accuracy. The accuracy is even better for the mixed oxide (NMC) and electrolyte (EC) datasets. The linear scaling model's capacity to probe thousands of points simultaneously permits calculation of $\rho(\vec{r})$ for large complex systems many orders of magnitude faster than DFT allowing screening of disordered functional materials.

Calibrated Uncertainty for Molecular Property Prediction using Ensembles of Message Passing Neural Networks

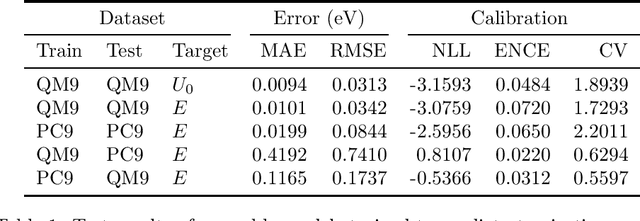
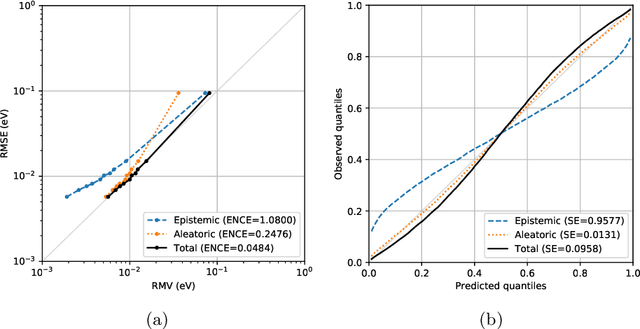
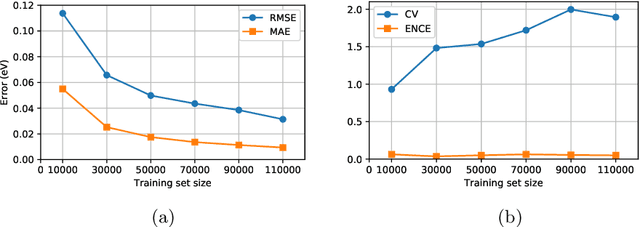
Data-driven methods based on machine learning have the potential to accelerate analysis of atomic structures. However, machine learning models can produce overconfident predictions and it is therefore crucial to detect and handle uncertainty carefully. Here, we extend a message passing neural network designed specifically for predicting properties of molecules and materials with a calibrated probabilistic predictive distribution. The method presented in this paper differs from the previous work by considering both aleatoric and epistemic uncertainty in a unified framework, and by re-calibrating the predictive distribution on unseen data. Through computer experiments, we show that our approach results in accurate models for predicting molecular formation energies with calibrated uncertainty in and out of the training data distribution on two public molecular benchmark datasets, QM9 and PC9. The proposed method provides a general framework for training and evaluating neural network ensemble models that are able to produce accurate predictions of properties of molecules with calibrated uncertainty.

DeepDFT: Neural Message Passing Network for Accurate Charge Density Prediction

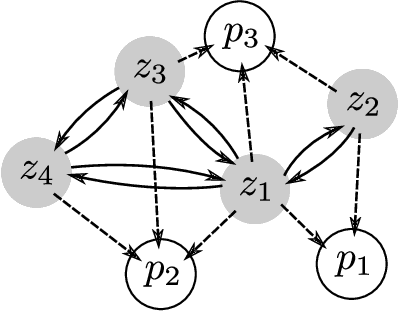
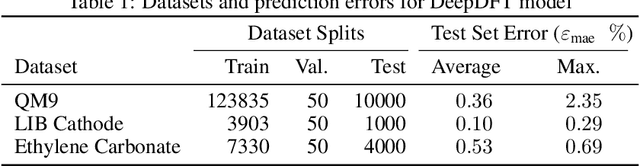
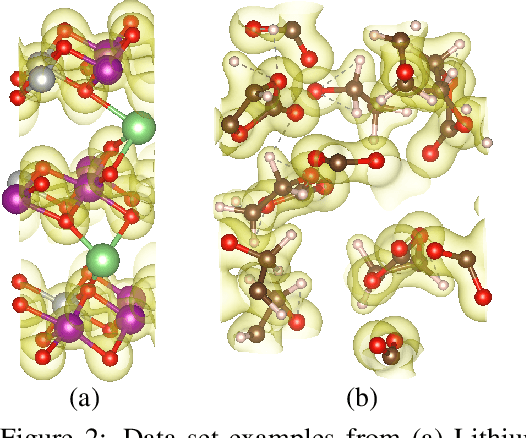
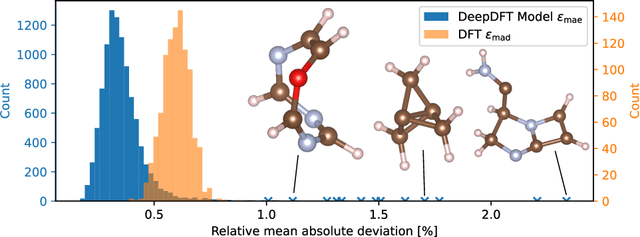
We introduce DeepDFT, a deep learning model for predicting the electronic charge density around atoms, the fundamental variable in electronic structure simulations from which all ground state properties can be calculated. The model is formulated as neural message passing on a graph, consisting of interacting atom vertices and special query point vertices for which the charge density is predicted. The accuracy and scalability of the model are demonstrated for molecules, solids and liquids. The trained model achieves lower average prediction errors than the observed variations in charge density obtained from density functional theory simulations using different exchange correlation functionals.