Graph neural networks for fast electron density estimation of molecules, liquids, and solids

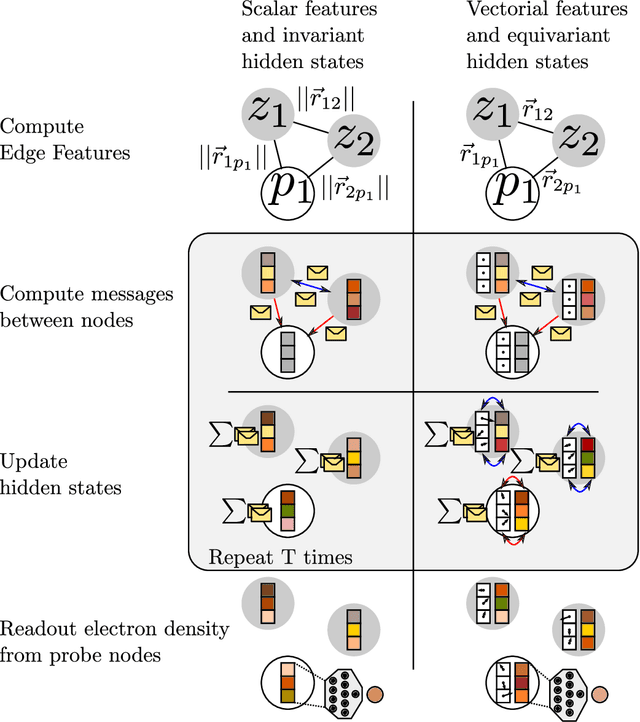
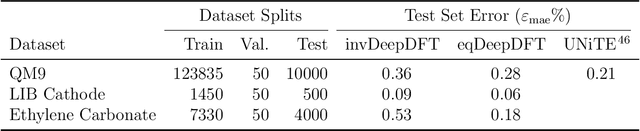
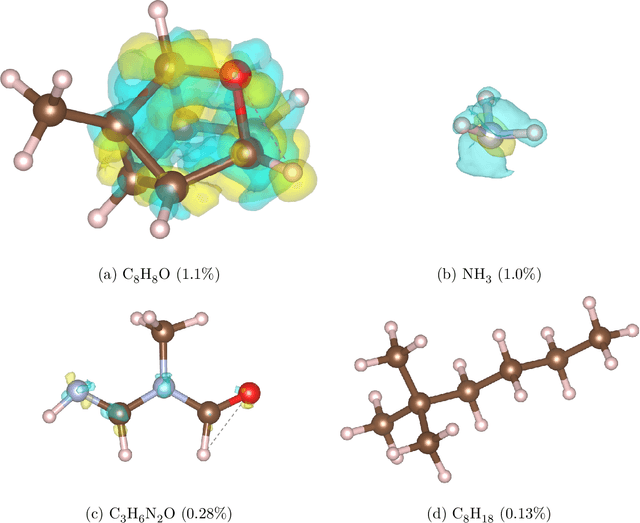
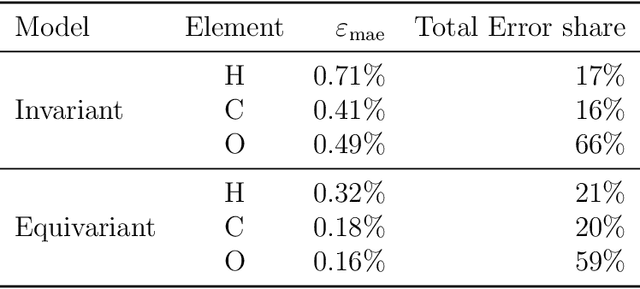
Electron density $\rho(\vec{r})$ is the fundamental variable in the calculation of ground state energy with density functional theory (DFT). Beyond total energy, features in $\rho(\vec{r})$ distribution and modifications in $\rho(\vec{r})$ are often used to capture critical physicochemical phenomena in functional materials and molecules at the electronic scale. Methods providing access to $\rho(\vec{r})$ of complex disordered systems with little computational cost can be a game changer in the expedited exploration of materials phase space towards the inverse design of new materials with better functionalities. We present a machine learning framework for the prediction of $\rho(\vec{r})$. The model is based on equivariant graph neural networks and the electron density is predicted at special query point vertices that are part of the message passing graph, but only receive messages. The model is tested across multiple data sets of molecules (QM9), liquid ethylene carbonate electrolyte (EC) and LixNiyMnzCo(1-y-z)O2 lithium ion battery cathodes (NMC). For QM9 molecules, the accuracy of the proposed model exceeds typical variability in $\rho(\vec{r})$ obtained from DFT done with different exchange-correlation functional and show beyond the state of the art accuracy. The accuracy is even better for the mixed oxide (NMC) and electrolyte (EC) datasets. The linear scaling model's capacity to probe thousands of points simultaneously permits calculation of $\rho(\vec{r})$ for large complex systems many orders of magnitude faster than DFT allowing screening of disordered functional materials.