Multi-Modal Multi-Task (M3T) Federated Foundation Models for Embodied AI: Potentials and Challenges for Edge Integration

As embodied AI systems become increasingly multi-modal, personalized, and interactive, they must learn effectively from diverse sensory inputs, adapt continually to user preferences, and operate safely under resource and privacy constraints. These challenges expose a pressing need for machine learning models capable of swift, context-aware adaptation while balancing model generalization and personalization. Here, two methods emerge as suitable candidates, each offering parts of these capabilities: Foundation Models (FMs) provide a pathway toward generalization across tasks and modalities, whereas Federated Learning (FL) offers the infrastructure for distributed, privacy-preserving model updates and user-level model personalization. However, when used in isolation, each of these approaches falls short of meeting the complex and diverse capability requirements of real-world embodied environments. In this vision paper, we introduce Federated Foundation Models (FFMs) for embodied AI, a new paradigm that unifies the strengths of multi-modal multi-task (M3T) FMs with the privacy-preserving distributed nature of FL, enabling intelligent systems at the wireless edge. We collect critical deployment dimensions of FFMs in embodied AI ecosystems under a unified framework, which we name "EMBODY": Embodiment heterogeneity, Modality richness and imbalance, Bandwidth and compute constraints, On-device continual learning, Distributed control and autonomy, and Yielding safety, privacy, and personalization. For each, we identify concrete challenges and envision actionable research directions. We also present an evaluation framework for deploying FFMs in embodied AI systems, along with the associated trade-offs.

An Automated Reinforcement Learning Reward Design Framework with Large Language Model for Cooperative Platoon Coordination

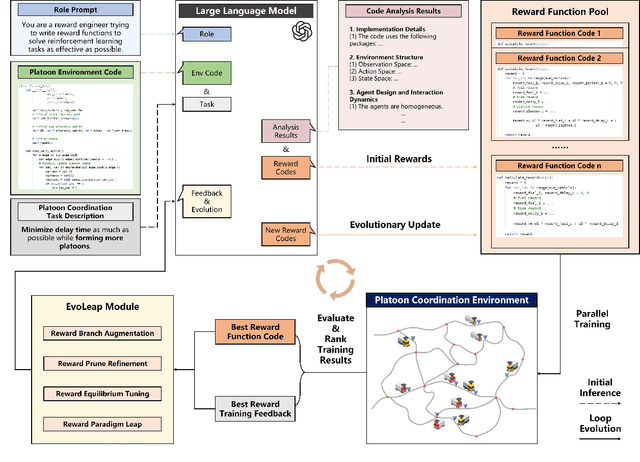
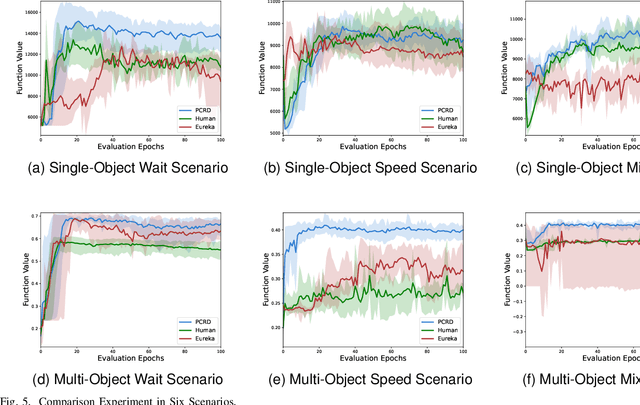
Reinforcement Learning (RL) has demonstrated excellent decision-making potential in platoon coordination problems. However, due to the variability of coordination goals, the complexity of the decision problem, and the time-consumption of trial-and-error in manual design, finding a well performance reward function to guide RL training to solve complex platoon coordination problems remains challenging. In this paper, we formally define the Platoon Coordination Reward Design Problem (PCRDP), extending the RL-based cooperative platoon coordination problem to incorporate automated reward function generation. To address PCRDP, we propose a Large Language Model (LLM)-based Platoon coordination Reward Design (PCRD) framework, which systematically automates reward function discovery through LLM-driven initialization and iterative optimization. In this method, LLM first initializes reward functions based on environment code and task requirements with an Analysis and Initial Reward (AIR) module, and then iteratively optimizes them based on training feedback with an evolutionary module. The AIR module guides LLM to deepen their understanding of code and tasks through a chain of thought, effectively mitigating hallucination risks in code generation. The evolutionary module fine-tunes and reconstructs the reward function, achieving a balance between exploration diversity and convergence stability for training. To validate our approach, we establish six challenging coordination scenarios with varying complexity levels within the Yangtze River Delta transportation network simulation. Comparative experimental results demonstrate that RL agents utilizing PCRD-generated reward functions consistently outperform human-engineered reward functions, achieving an average of 10\% higher performance metrics in all scenarios.

Adaptive UAV-Assisted Hierarchical Federated Learning: Optimizing Energy, Latency, and Resilience for Dynamic Smart IoT Networks

Hierarchical Federated Learning (HFL) introduces intermediate aggregation layers, addressing the limitations of conventional Federated Learning (FL) in geographically dispersed environments with limited communication infrastructure. An application of HFL is in smart IoT systems, such as remote monitoring, disaster response, and battlefield operations, where cellular connectivity is often unreliable or unavailable. In these scenarios, UAVs serve as mobile aggregators, providing connectivity to the terrestrial IoT devices. This paper studies an HFL architecture for energy-constrained UAVs in smart IoT systems, pioneering a solution to minimize global training cost increased caused by UAV disconnection. In light of this, we formulate a joint optimization problem involving learning configuration, bandwidth allocation, and device-to-UAV association, and perform global aggregation in time before UAV drops disconnect and redeployment of UAVs. The problem explicitly accounts for the dynamic nature of IoT devices and their interruptible communications and is unveiled to be NP-hard. To address this, we decompose it into three subproblems. First, we optimize the learning configuration and bandwidth allocation using an augmented Lagrangian function to reduce training costs. Second, we propose a device fitness score, integrating data heterogeneity (via Kullback-Leibler divergence), device-to-UAV distances, and IoT device resources, and develop a twin-delayed deep deterministic policy gradient (TD3)-based algorithm for dynamic device-to-UAV assignment. Third, We introduce a low-complexity two-stage greedy strategy for finding the location of UAVs redeployment and selecting the appropriate global aggregator UAV. Experiments on real-world datasets demonstrate significant cost reductions and robust performance under communication interruptions.

Multi-Vehicle Trajectory Planning at V2I-enabled Intersections based on Correlated Equilibrium

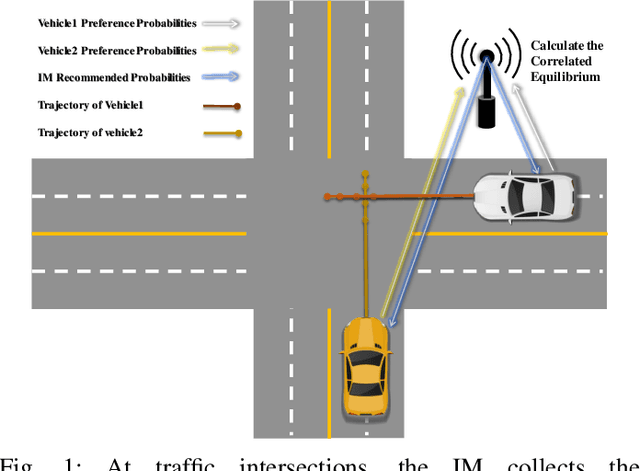
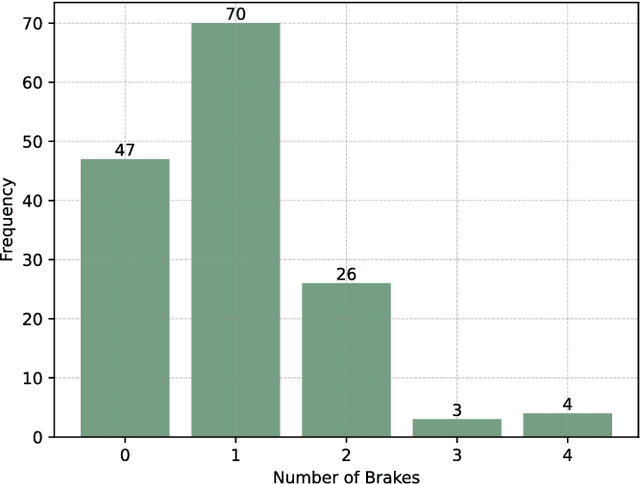
Generating trajectories that ensure both vehicle safety and improve traffic efficiency remains a challenging task at intersections. Many existing works utilize Nash equilibrium (NE) for the trajectory planning at intersections. However, NE-based planning can hardly guarantee that all vehicles are in the same equilibrium, leading to a risk of collision. In this work, we propose a framework for trajectory planning based on Correlated Equilibrium (CE) when V2I communication is also enabled. The recommendation with CE allows all vehicles to reach a safe and consensual equilibrium and meanwhile keeps the rationality as NE-based methods that no vehicle has the incentive to deviate. The Intersection Manager (IM) first collects the trajectory library and the personal preference probabilities over the library from each vehicle in a low-resolution spatial-temporal grid map. Then, the IM optimizes the recommendation probability distribution for each vehicle's trajectory by minimizing overall collision probability under the CE constraint. Finally, each vehicle samples a trajectory of the low-resolution map to construct a safety corridor and derive a smooth trajectory with a local refinement optimization. We conduct comparative experiments at a crossroad intersection involving two and four vehicles, validating the effectiveness of our method in balancing vehicle safety and traffic efficiency.

Distributed Fractional Bayesian Learning for Adaptive Optimization

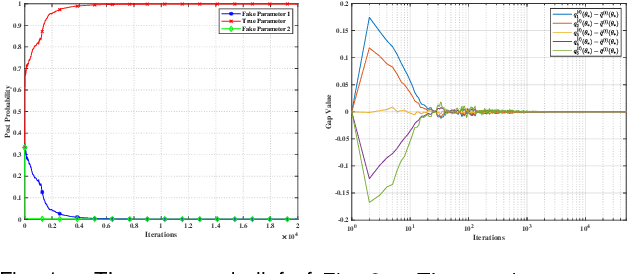
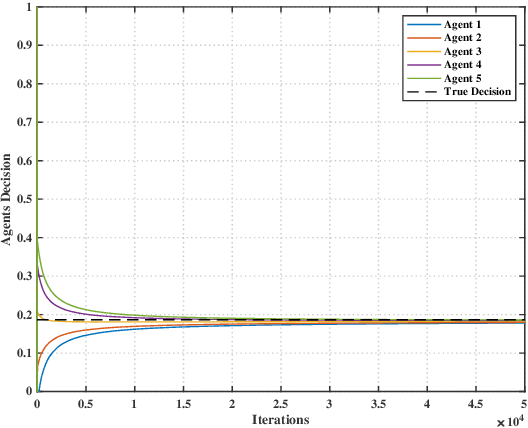
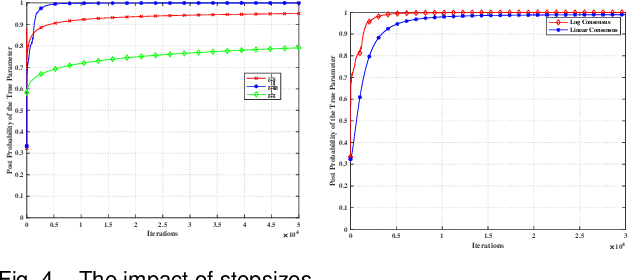
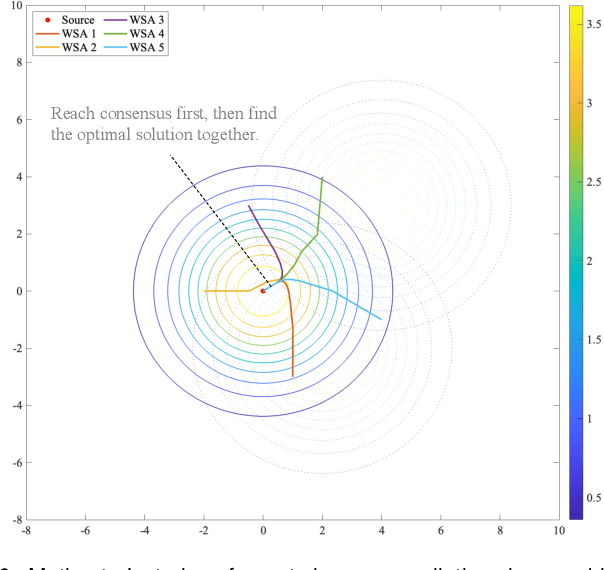
This paper considers a distributed adaptive optimization problem, where all agents only have access to their local cost functions with a common unknown parameter, whereas they mean to collaboratively estimate the true parameter and find the optimal solution over a connected network. A general mathematical framework for such a problem has not been studied yet. We aim to provide valuable insights for addressing parameter uncertainty in distributed optimization problems and simultaneously find the optimal solution. Thus, we propose a novel Prediction while Optimization scheme, which utilizes distributed fractional Bayesian learning through weighted averaging on the log-beliefs to update the beliefs of unknown parameters, and distributed gradient descent for renewing the estimation of the optimal solution. Then under suitable assumptions, we prove that all agents' beliefs and decision variables converge almost surely to the true parameter and the optimal solution under the true parameter, respectively. We further establish a sublinear convergence rate for the belief sequence. Finally, numerical experiments are implemented to corroborate the theoretical analysis.

Distributed Pose-graph Optimization with Multi-level Partitioning for Collaborative SLAM

The back-end module of Distributed Collaborative Simultaneous Localization and Mapping (DCSLAM) requires solving a nonlinear Pose Graph Optimization (PGO) under a distributed setting, also known as SE(d)-synchronization. Most existing distributed graph optimization algorithms employ a simple sequential partitioning scheme, which may result in unbalanced subgraph dimensions due to the different geographic locations of each robot, and hence imposes extra communication load. Moreover, the performance of current Riemannian optimization algorithms can be further accelerated. In this letter, we propose a novel distributed pose graph optimization algorithm combining multi-level partitioning with an accelerated Riemannian optimization method. Firstly, we employ the multi-level graph partitioning algorithm to preprocess the naive pose graph to formulate a balanced optimization problem. In addition, inspired by the accelerated coordinate descent method, we devise an Improved Riemannian Block Coordinate Descent (IRBCD) algorithm and the critical point obtained is globally optimal. Finally, we evaluate the effects of four common graph partitioning approaches on the correlation of the inter-subgraphs, and discover that the Highest scheme has the best partitioning performance. Also, we implement simulations to quantitatively demonstrate that our proposed algorithm outperforms the state-of-the-art distributed pose graph optimization protocols.

Online Parameter Identification of Generalized Non-cooperative Game

This work studies the parameter identification problem of a generalized non-cooperative game, where each player's cost function is influenced by an observable signal and some unknown parameters. We consider the scenario where equilibrium of the game at some observable signals can be observed with noises, whereas our goal is to identify the unknown parameters with the observed data. Assuming that the observable signals and the corresponding noise-corrupted equilibriums are acquired sequentially, we construct this parameter identification problem as online optimization and introduce a novel online parameter identification algorithm. To be specific, we construct a regularized loss function that balances conservativeness and correctiveness, where the conservativeness term ensures that the new estimates do not deviate significantly from the current estimates, while the correctiveness term is captured by the Karush-Kuhn-Tucker conditions. We then prove that when the players' cost functions are linear with respect to the unknown parameters and the learning rate of the online parameter identification algorithm satisfies \mu_k \propto 1/\sqrt{k}, along with other assumptions, the regret bound of the proposed algorithm is O(\sqrt{K}). Finally, we conduct numerical simulations on a Nash-Cournot problem to demonstrate that the performance of the online identification algorithm is comparable to that of the offline setting.

Distributed Online Convex Optimization with Adversarial Constraints: Reduced Cumulative Constraint Violation Bounds under Slater's Condition

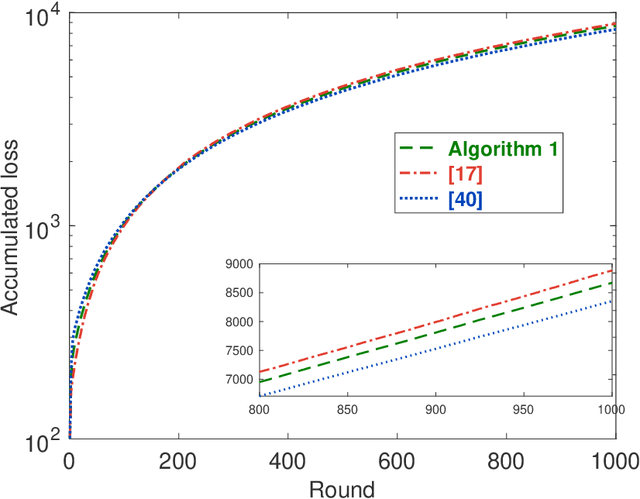
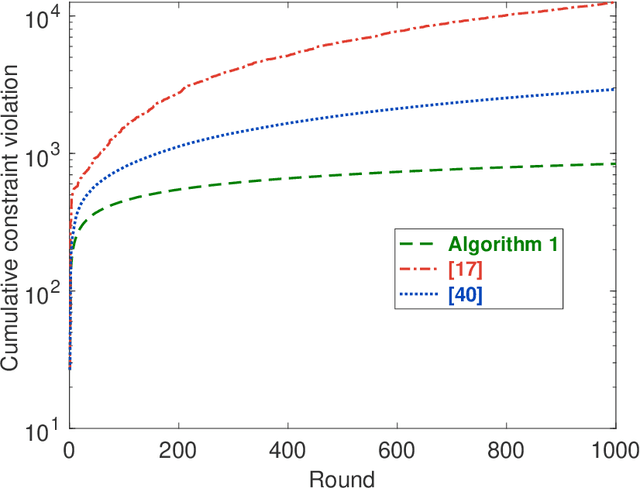
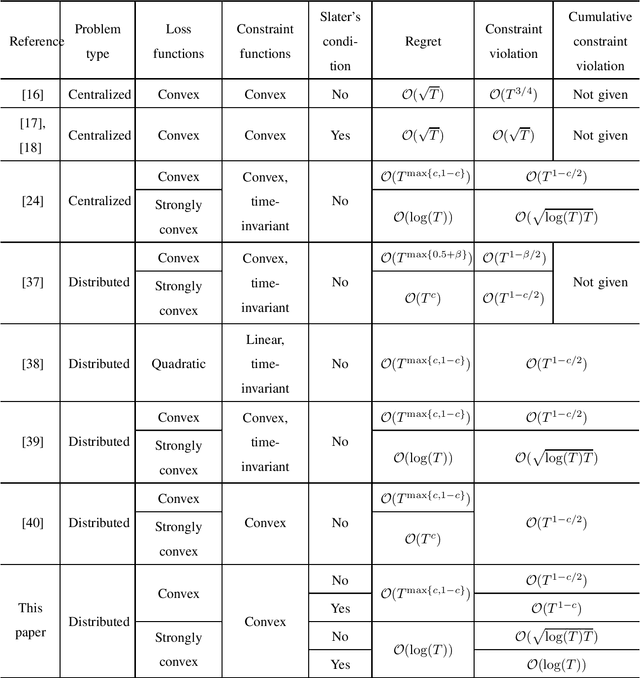
This paper considers distributed online convex optimization with adversarial constraints. In this setting, a network of agents makes decisions at each round, and then only a portion of the loss function and a coordinate block of the constraint function are privately revealed to each agent. The loss and constraint functions are convex and can vary arbitrarily across rounds. The agents collaborate to minimize network regret and cumulative constraint violation. A novel distributed online algorithm is proposed and it achieves an $\mathcal{O}(T^{\max\{c,1-c\}})$ network regret bound and an $\mathcal{O}(T^{1-c/2})$ network cumulative constraint violation bound, where $T$ is the number of rounds and $c\in(0,1)$ is a user-defined trade-off parameter. When Slater's condition holds (i.e, there is a point that strictly satisfies the inequality constraints), the network cumulative constraint violation bound is reduced to $\mathcal{O}(T^{1-c})$. Moreover, if the loss functions are strongly convex, then the network regret bound is reduced to $\mathcal{O}(\log(T))$, and the network cumulative constraint violation bound is reduced to $\mathcal{O}(\sqrt{\log(T)T})$ and $\mathcal{O}(\log(T))$ without and with Slater's condition, respectively. To the best of our knowledge, this paper is the first to achieve reduced (network) cumulative constraint violation bounds for (distributed) online convex optimization with adversarial constraints under Slater's condition. Finally, the theoretical results are verified through numerical simulations.

Global Nash Equilibrium in Non-convex Multi-player Game: Theory and Algorithms

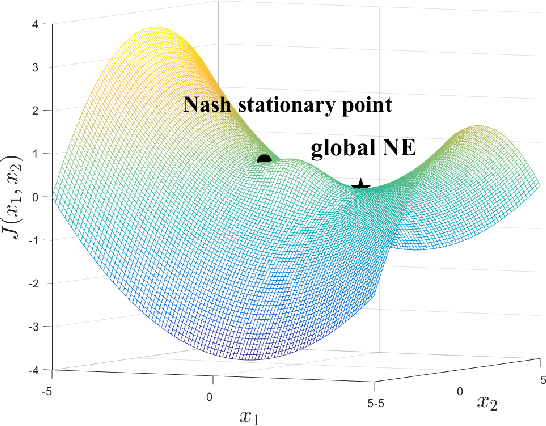
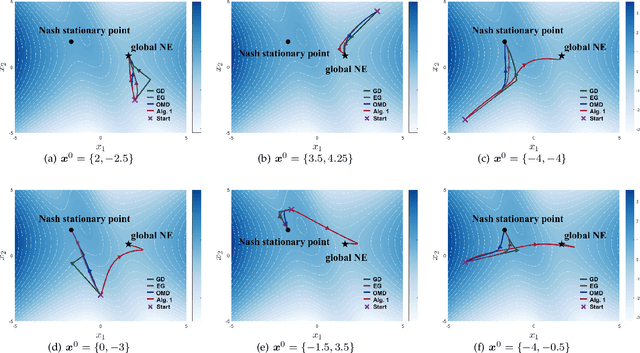
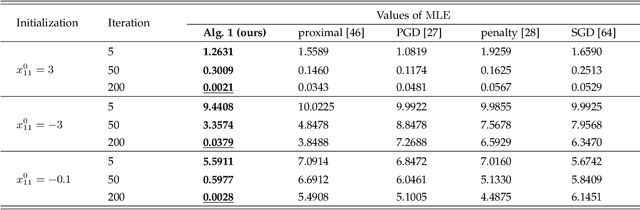
Wide machine learning tasks can be formulated as non-convex multi-player games, where Nash equilibrium (NE) is an acceptable solution to all players, since no one can benefit from changing its strategy unilaterally. Attributed to the non-convexity, obtaining the existence condition of global NE is challenging, let alone designing theoretically guaranteed realization algorithms. This paper takes conjugate transformation to the formulation of non-convex multi-player games, and casts the complementary problem into a variational inequality (VI) problem with a continuous pseudo-gradient mapping. We then prove the existence condition of global NE: the solution to the VI problem satisfies a duality relation. Based on this VI formulation, we design a conjugate-based ordinary differential equation (ODE) to approach global NE, which is proved to have an exponential convergence rate. To make the dynamics more implementable, we further derive a discretized algorithm. We apply our algorithm to two typical scenarios: multi-player generalized monotone game and multi-player potential game. In the two settings, we prove that the step-size setting is required to be $\mathcal{O}(1/k)$ and $\mathcal{O}(1/\sqrt k)$ to yield the convergence rates of $\mathcal{O}(1/ k)$ and $\mathcal{O}(1/\sqrt k)$, respectively. Extensive experiments in robust neural network training and sensor localization are in full agreement with our theory.

A Survey of Decision Making in Adversarial Games

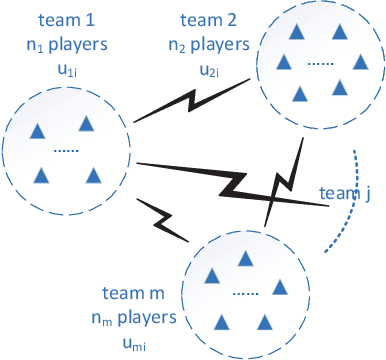
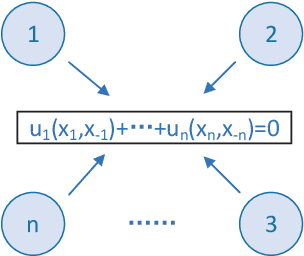
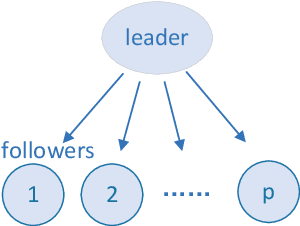
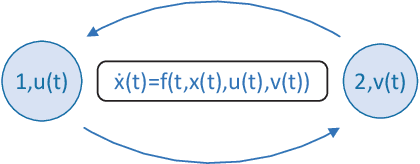
Game theory has by now found numerous applications in various fields, including economics, industry, jurisprudence, and artificial intelligence, where each player only cares about its own interest in a noncooperative or cooperative manner, but without obvious malice to other players. However, in many practical applications, such as poker, chess, evader pursuing, drug interdiction, coast guard, cyber-security, and national defense, players often have apparently adversarial stances, that is, selfish actions of each player inevitably or intentionally inflict loss or wreak havoc on other players. Along this line, this paper provides a systematic survey on three main game models widely employed in adversarial games, i.e., zero-sum normal-form and extensive-form games, Stackelberg (security) games, zero-sum differential games, from an array of perspectives, including basic knowledge of game models, (approximate) equilibrium concepts, problem classifications, research frontiers, (approximate) optimal strategy seeking techniques, prevailing algorithms, and practical applications. Finally, promising future research directions are also discussed for relevant adversarial games.