Distributed Fractional Bayesian Learning for Adaptive Optimization
Paper and Code
Apr 17, 2024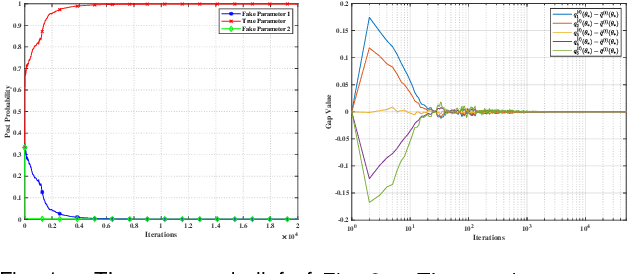
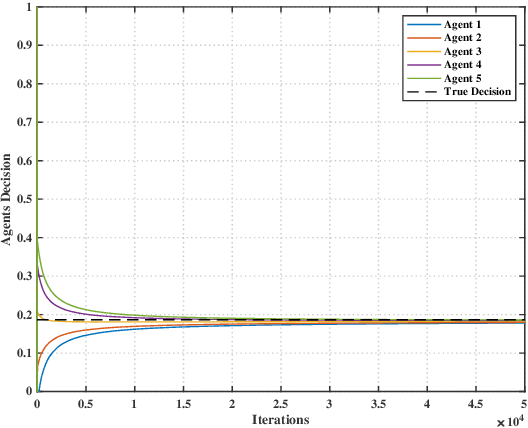
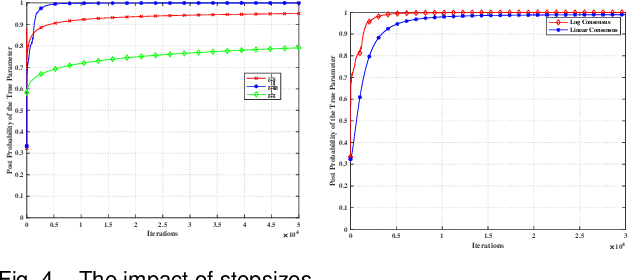
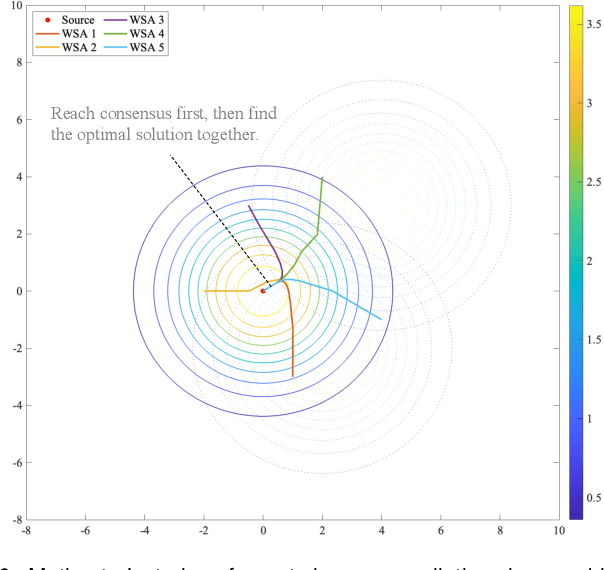
This paper considers a distributed adaptive optimization problem, where all agents only have access to their local cost functions with a common unknown parameter, whereas they mean to collaboratively estimate the true parameter and find the optimal solution over a connected network. A general mathematical framework for such a problem has not been studied yet. We aim to provide valuable insights for addressing parameter uncertainty in distributed optimization problems and simultaneously find the optimal solution. Thus, we propose a novel Prediction while Optimization scheme, which utilizes distributed fractional Bayesian learning through weighted averaging on the log-beliefs to update the beliefs of unknown parameters, and distributed gradient descent for renewing the estimation of the optimal solution. Then under suitable assumptions, we prove that all agents' beliefs and decision variables converge almost surely to the true parameter and the optimal solution under the true parameter, respectively. We further establish a sublinear convergence rate for the belief sequence. Finally, numerical experiments are implemented to corroborate the theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge