Rate Analysis of Coupled Distributed Stochastic Approximation for Misspecified Optimization

We consider an $n$ agents distributed optimization problem with imperfect information characterized in a parametric sense, where the unknown parameter can be solved by a distinct distributed parameter learning problem. Though each agent only has access to its local parameter learning and computational problem, they mean to collaboratively minimize the average of their local cost functions. To address the special optimization problem, we propose a coupled distributed stochastic approximation algorithm, in which every agent updates the current beliefs of its unknown parameter and decision variable by stochastic approximation method; and then averages the beliefs and decision variables of its neighbors over network in consensus protocol. Our interest lies in the convergence analysis of this algorithm. We quantitatively characterize the factors that affect the algorithm performance, and prove that the mean-squared error of the decision variable is bounded by $\mathcal{O}(\frac{1}{nk})+\mathcal{O}\left(\frac{1}{\sqrt{n}(1-\rho_w)}\right)\frac{1}{k^{1.5}}+\mathcal{O}\big(\frac{1}{(1-\rho_w)^2} \big)\frac{1}{k^2}$, where $k$ is the iteration count and $(1-\rho_w)$ is the spectral gap of the network weighted adjacency matrix. It reveals that the network connectivity characterized by $(1-\rho_w)$ only influences the high order of convergence rate, while the domain rate still acts the same as the centralized algorithm. In addition, we analyze that the transient iteration needed for reaching its dominant rate $\mathcal{O}(\frac{1}{nk})$ is $\mathcal{O}(\frac{n}{(1-\rho_w)^2})$. Numerical experiments are carried out to demonstrate the theoretical results by taking different CPUs as agents, which is more applicable to real-world distributed scenarios.

Distributed Fractional Bayesian Learning for Adaptive Optimization

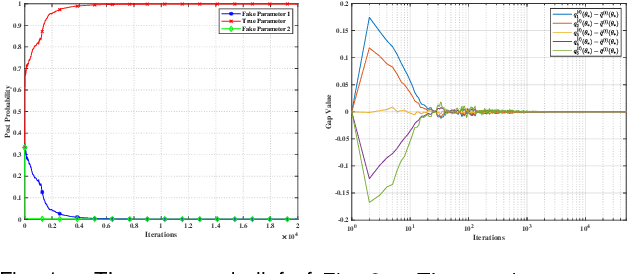
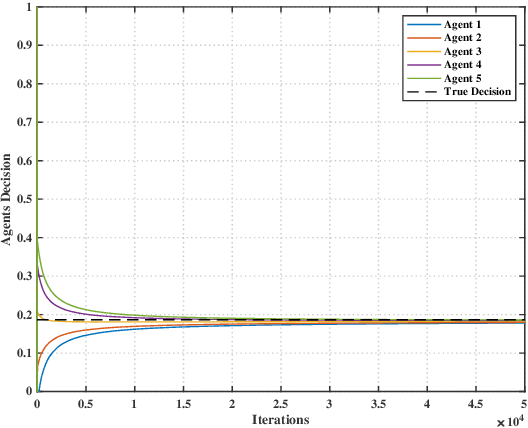
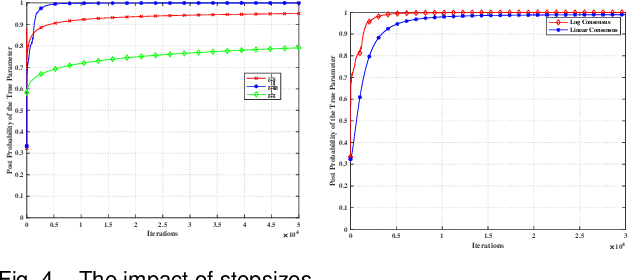
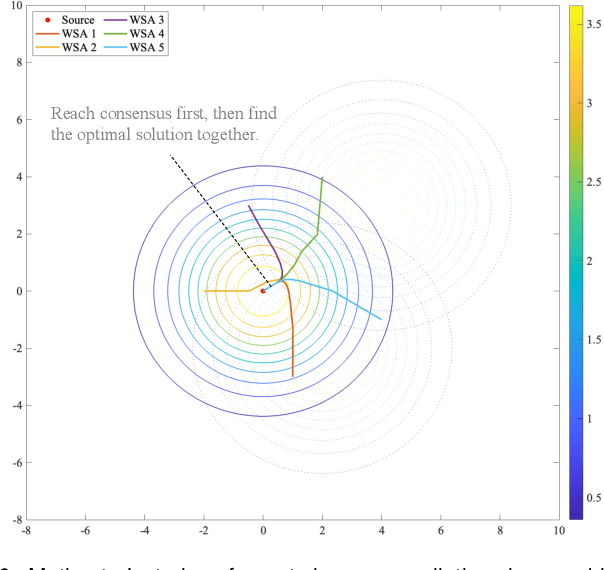
This paper considers a distributed adaptive optimization problem, where all agents only have access to their local cost functions with a common unknown parameter, whereas they mean to collaboratively estimate the true parameter and find the optimal solution over a connected network. A general mathematical framework for such a problem has not been studied yet. We aim to provide valuable insights for addressing parameter uncertainty in distributed optimization problems and simultaneously find the optimal solution. Thus, we propose a novel Prediction while Optimization scheme, which utilizes distributed fractional Bayesian learning through weighted averaging on the log-beliefs to update the beliefs of unknown parameters, and distributed gradient descent for renewing the estimation of the optimal solution. Then under suitable assumptions, we prove that all agents' beliefs and decision variables converge almost surely to the true parameter and the optimal solution under the true parameter, respectively. We further establish a sublinear convergence rate for the belief sequence. Finally, numerical experiments are implemented to corroborate the theoretical analysis.