Jinlong Lei
HGFormer: A Hierarchical Graph Transformer Framework for Two-Stage Colonel Blotto Games via Reinforcement Learning
Jun 10, 2025Abstract:Two-stage Colonel Blotto game represents a typical adversarial resource allocation problem, in which two opposing agents sequentially allocate resources in a network topology across two phases: an initial resource deployment followed by multiple rounds of dynamic reallocation adjustments. The sequential dependency between game stages and the complex constraints imposed by the graph topology make it difficult for traditional approaches to attain a globally optimal strategy. To address these challenges, we propose a hierarchical graph Transformer framework called HGformer. By incorporating an enhanced graph Transformer encoder with structural biases and a two-agent hierarchical decision model, our approach enables efficient policy generation in large-scale adversarial environments. Moreover, we design a layer-by-layer feedback reinforcement learning algorithm that feeds the long-term returns from lower-level decisions back into the optimization of the higher-level strategy, thus bridging the coordination gap between the two decision-making stages. Experimental results demonstrate that, compared to existing hierarchical decision-making or graph neural network methods, HGformer significantly improves resource allocation efficiency and adversarial payoff, achieving superior overall performance in complex dynamic game scenarios.
An Automated Reinforcement Learning Reward Design Framework with Large Language Model for Cooperative Platoon Coordination
Apr 28, 2025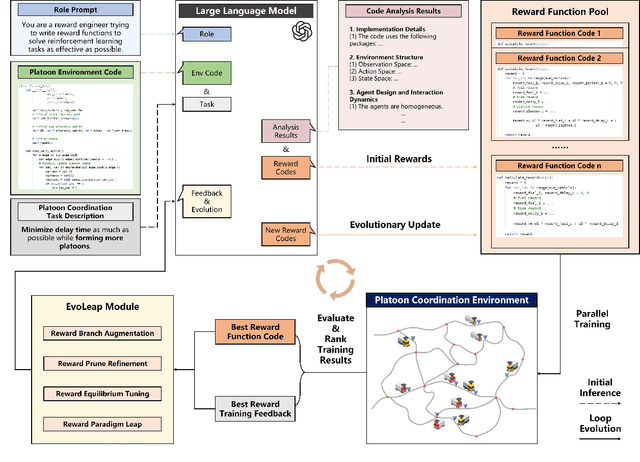

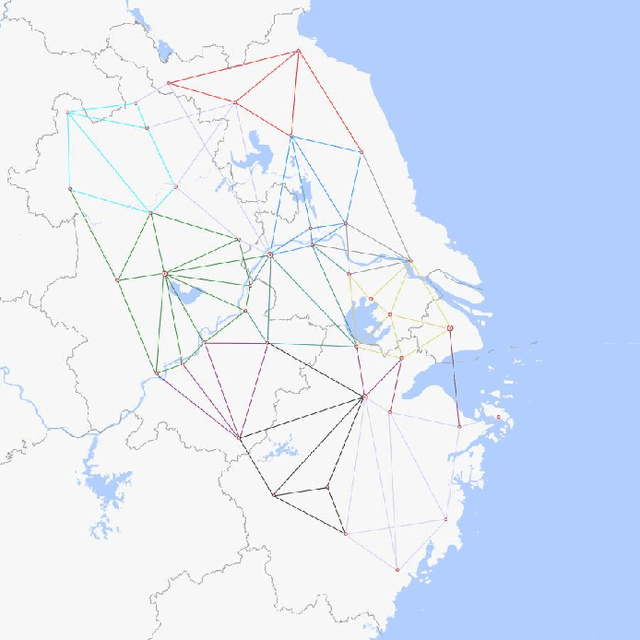
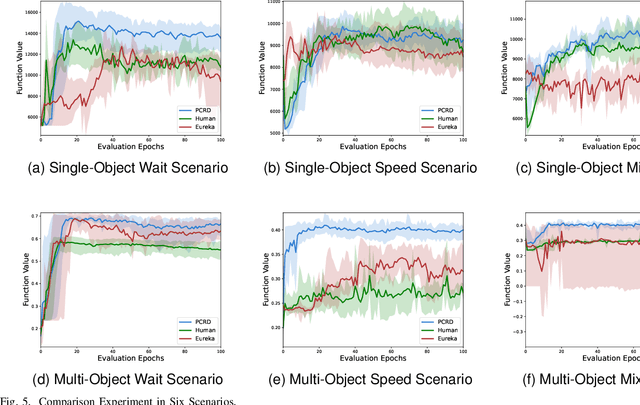
Abstract:Reinforcement Learning (RL) has demonstrated excellent decision-making potential in platoon coordination problems. However, due to the variability of coordination goals, the complexity of the decision problem, and the time-consumption of trial-and-error in manual design, finding a well performance reward function to guide RL training to solve complex platoon coordination problems remains challenging. In this paper, we formally define the Platoon Coordination Reward Design Problem (PCRDP), extending the RL-based cooperative platoon coordination problem to incorporate automated reward function generation. To address PCRDP, we propose a Large Language Model (LLM)-based Platoon coordination Reward Design (PCRD) framework, which systematically automates reward function discovery through LLM-driven initialization and iterative optimization. In this method, LLM first initializes reward functions based on environment code and task requirements with an Analysis and Initial Reward (AIR) module, and then iteratively optimizes them based on training feedback with an evolutionary module. The AIR module guides LLM to deepen their understanding of code and tasks through a chain of thought, effectively mitigating hallucination risks in code generation. The evolutionary module fine-tunes and reconstructs the reward function, achieving a balance between exploration diversity and convergence stability for training. To validate our approach, we establish six challenging coordination scenarios with varying complexity levels within the Yangtze River Delta transportation network simulation. Comparative experimental results demonstrate that RL agents utilizing PCRD-generated reward functions consistently outperform human-engineered reward functions, achieving an average of 10\% higher performance metrics in all scenarios.
A Local Information Aggregation based Multi-Agent Reinforcement Learning for Robot Swarm Dynamic Task Allocation
Nov 29, 2024



Abstract:In this paper, we explore how to optimize task allocation for robot swarms in dynamic environments, emphasizing the necessity of formulating robust, flexible, and scalable strategies for robot cooperation. We introduce a novel framework using a decentralized partially observable Markov decision process (Dec_POMDP), specifically designed for distributed robot swarm networks. At the core of our methodology is the Local Information Aggregation Multi-Agent Deep Deterministic Policy Gradient (LIA_MADDPG) algorithm, which merges centralized training with distributed execution (CTDE). During the centralized training phase, a local information aggregation (LIA) module is meticulously designed to gather critical data from neighboring robots, enhancing decision-making efficiency. In the distributed execution phase, a strategy improvement method is proposed to dynamically adjust task allocation based on changing and partially observable environmental conditions. Our empirical evaluations show that the LIA module can be seamlessly integrated into various CTDE-based MARL methods, significantly enhancing their performance. Additionally, by comparing LIA_MADDPG with six conventional reinforcement learning algorithms and a heuristic algorithm, we demonstrate its superior scalability, rapid adaptation to environmental changes, and ability to maintain both stability and convergence speed. These results underscore LIA_MADDPG's outstanding performance and its potential to significantly improve dynamic task allocation in robot swarms through enhanced local collaboration and adaptive strategy execution.
A Semi-decentralized and Variational-Equilibrium-Based Trajectory Planner for Connected and Autonomous Vehicles
Oct 20, 2024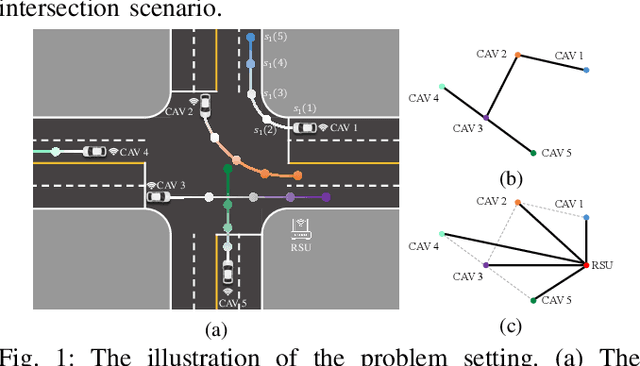
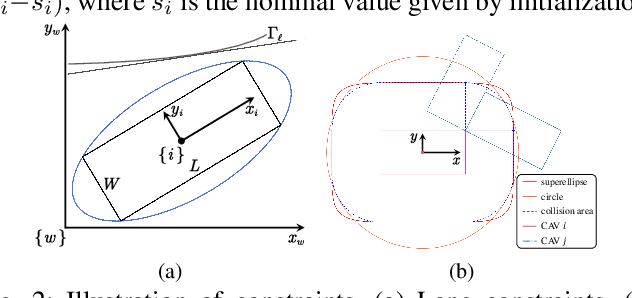
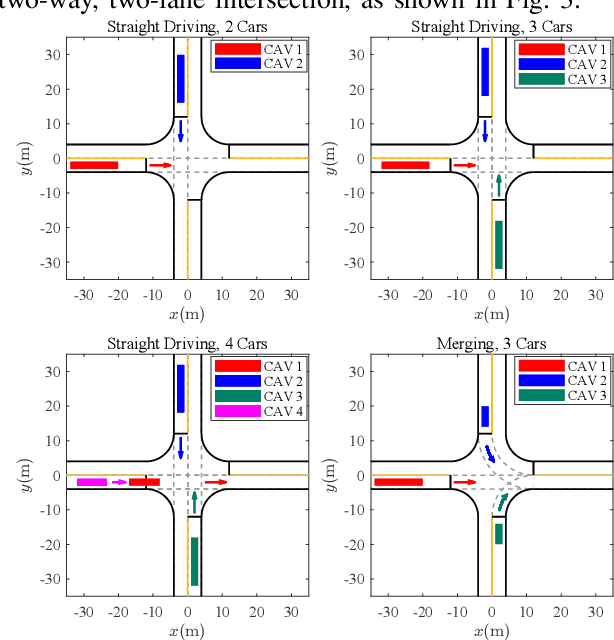
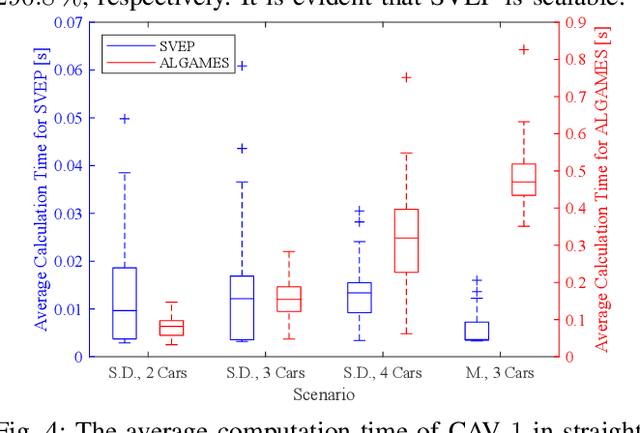
Abstract:This paper designs a novel trajectory planning approach to resolve the computational efficiency and safety problems in uncoordinated methods by exploiting vehicle-to-everything (V2X) technology. The trajectory planning for connected and autonomous vehicles (CAVs) is formulated as a game with coupled safety constraints. We then define interaction-fair trajectories and prove that they correspond to the variational equilibrium (VE) of this game. We propose a semi-decentralized planner for the vehicles to seek VE-based fair trajectories, which can significantly improve computational efficiency through parallel computing among CAVs and enhance the safety of planned trajectories by ensuring equilibrium concordance among CAVs. Finally, experimental results show the advantages of the approach, including fast computation speed, high scalability, equilibrium concordance, and safety.
Rate Analysis of Coupled Distributed Stochastic Approximation for Misspecified Optimization
Apr 21, 2024Abstract:We consider an $n$ agents distributed optimization problem with imperfect information characterized in a parametric sense, where the unknown parameter can be solved by a distinct distributed parameter learning problem. Though each agent only has access to its local parameter learning and computational problem, they mean to collaboratively minimize the average of their local cost functions. To address the special optimization problem, we propose a coupled distributed stochastic approximation algorithm, in which every agent updates the current beliefs of its unknown parameter and decision variable by stochastic approximation method; and then averages the beliefs and decision variables of its neighbors over network in consensus protocol. Our interest lies in the convergence analysis of this algorithm. We quantitatively characterize the factors that affect the algorithm performance, and prove that the mean-squared error of the decision variable is bounded by $\mathcal{O}(\frac{1}{nk})+\mathcal{O}\left(\frac{1}{\sqrt{n}(1-\rho_w)}\right)\frac{1}{k^{1.5}}+\mathcal{O}\big(\frac{1}{(1-\rho_w)^2} \big)\frac{1}{k^2}$, where $k$ is the iteration count and $(1-\rho_w)$ is the spectral gap of the network weighted adjacency matrix. It reveals that the network connectivity characterized by $(1-\rho_w)$ only influences the high order of convergence rate, while the domain rate still acts the same as the centralized algorithm. In addition, we analyze that the transient iteration needed for reaching its dominant rate $\mathcal{O}(\frac{1}{nk})$ is $\mathcal{O}(\frac{n}{(1-\rho_w)^2})$. Numerical experiments are carried out to demonstrate the theoretical results by taking different CPUs as agents, which is more applicable to real-world distributed scenarios.
Distributed Fractional Bayesian Learning for Adaptive Optimization
Apr 17, 2024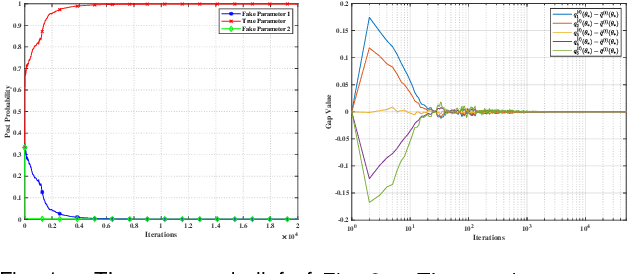
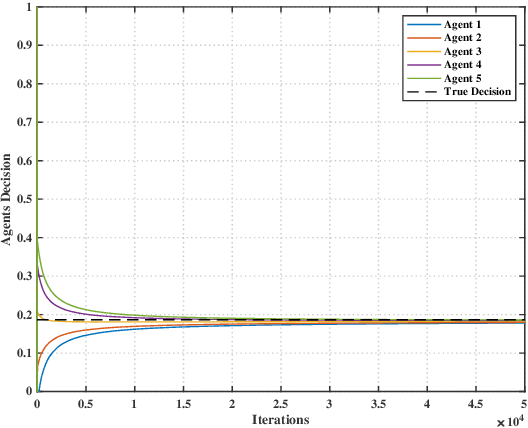
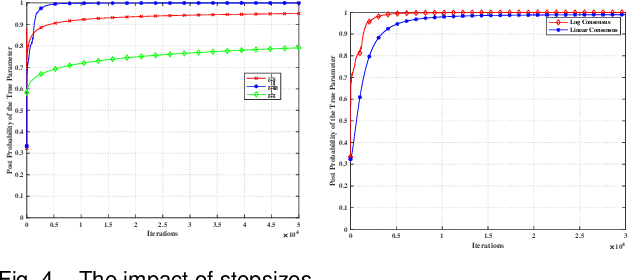
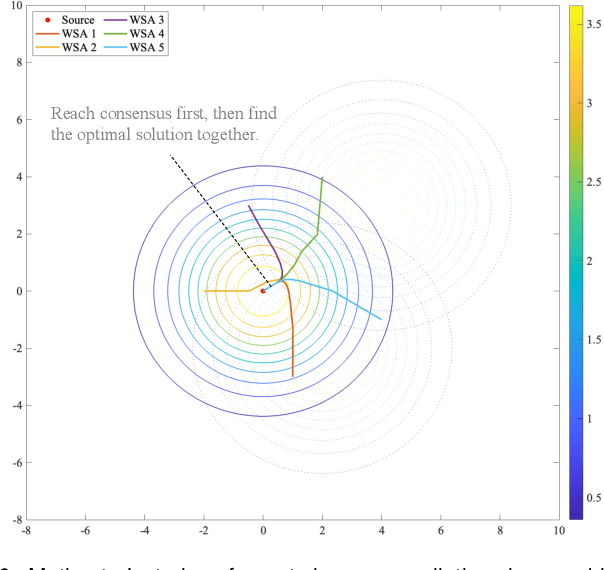
Abstract:This paper considers a distributed adaptive optimization problem, where all agents only have access to their local cost functions with a common unknown parameter, whereas they mean to collaboratively estimate the true parameter and find the optimal solution over a connected network. A general mathematical framework for such a problem has not been studied yet. We aim to provide valuable insights for addressing parameter uncertainty in distributed optimization problems and simultaneously find the optimal solution. Thus, we propose a novel Prediction while Optimization scheme, which utilizes distributed fractional Bayesian learning through weighted averaging on the log-beliefs to update the beliefs of unknown parameters, and distributed gradient descent for renewing the estimation of the optimal solution. Then under suitable assumptions, we prove that all agents' beliefs and decision variables converge almost surely to the true parameter and the optimal solution under the true parameter, respectively. We further establish a sublinear convergence rate for the belief sequence. Finally, numerical experiments are implemented to corroborate the theoretical analysis.
Online Parameter Identification of Generalized Non-cooperative Game
Oct 14, 2023


Abstract:This work studies the parameter identification problem of a generalized non-cooperative game, where each player's cost function is influenced by an observable signal and some unknown parameters. We consider the scenario where equilibrium of the game at some observable signals can be observed with noises, whereas our goal is to identify the unknown parameters with the observed data. Assuming that the observable signals and the corresponding noise-corrupted equilibriums are acquired sequentially, we construct this parameter identification problem as online optimization and introduce a novel online parameter identification algorithm. To be specific, we construct a regularized loss function that balances conservativeness and correctiveness, where the conservativeness term ensures that the new estimates do not deviate significantly from the current estimates, while the correctiveness term is captured by the Karush-Kuhn-Tucker conditions. We then prove that when the players' cost functions are linear with respect to the unknown parameters and the learning rate of the online parameter identification algorithm satisfies \mu_k \propto 1/\sqrt{k}, along with other assumptions, the regret bound of the proposed algorithm is O(\sqrt{K}). Finally, we conduct numerical simulations on a Nash-Cournot problem to demonstrate that the performance of the online identification algorithm is comparable to that of the offline setting.
No-regret learning for repeated non-cooperative games with lossy bandits
May 14, 2022
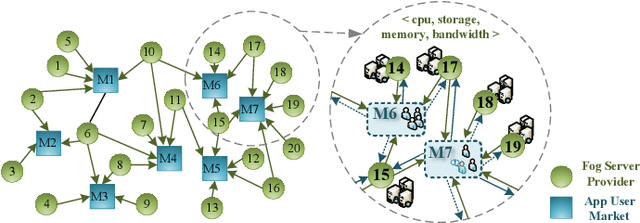
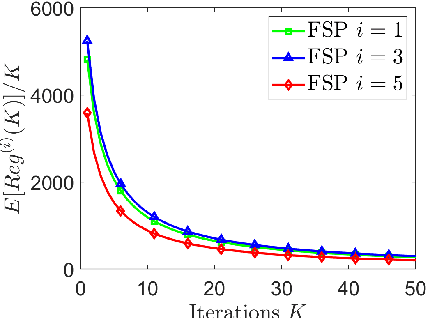
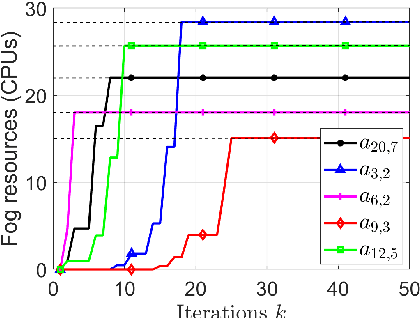
Abstract:This paper considers no-regret learning for repeated continuous-kernel games with lossy bandit feedback. Since it is difficult to give the explicit model of the utility functions in dynamic environments, the players' action can only be learned with bandit feedback. Moreover, because of unreliable communication channels or privacy protection, the bandit feedback may be lost or dropped at random. Therefore, we study the asynchronous online learning strategy of the players to adaptively adjust the next actions for minimizing the long-term regret loss. The paper provides a novel no-regret learning algorithm, called Online Gradient Descent with lossy bandits (OGD-lb). We first give the regret analysis for concave games with differentiable and Lipschitz utilities. Then we show that the action profile converges to a Nash equilibrium with probability 1 when the game is also strictly monotone. We further provide the mean square convergence rate $\mathcal{O}\left(k^{-2\min\{\beta, 1/6\}}\right)$ when the game is $\beta-$ strongly monotone. In addition, we extend the algorithm to the case when the loss probability of the bandit feedback is unknown, and prove its almost sure convergence to Nash equilibrium for strictly monotone games. Finally, we take the resource management in fog computing as an application example, and carry out numerical experiments to empirically demonstrate the algorithm performance.
Distributed Policy Gradient with Variance Reduction in Multi-Agent Reinforcement Learning
Nov 30, 2021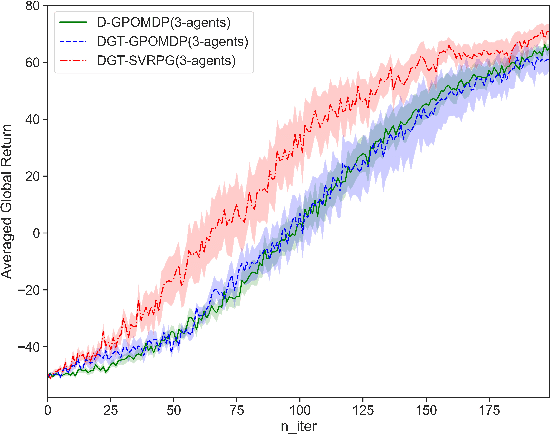
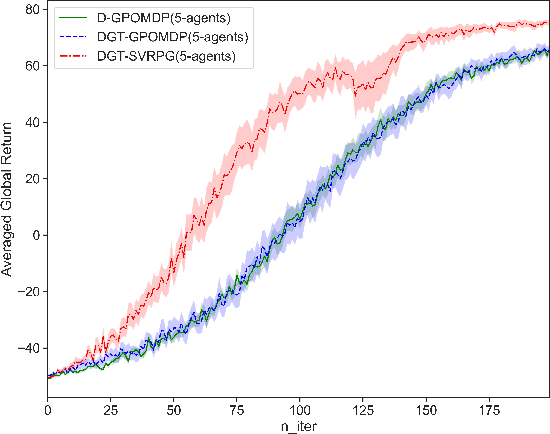
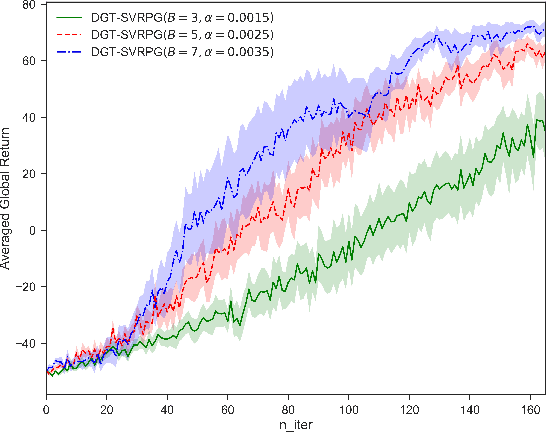
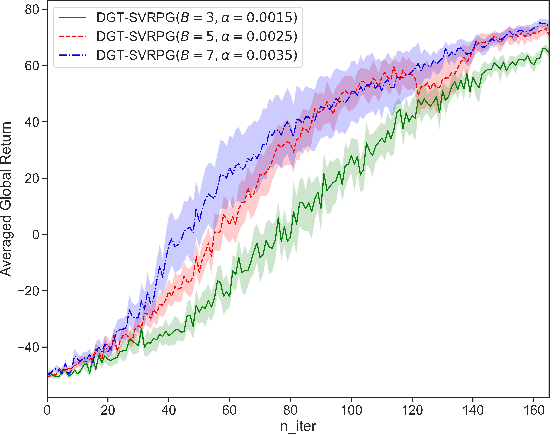
Abstract:This paper studies a distributed policy gradient in collaborative multi-agent reinforcement learning (MARL), where agents over a communication network aim to find the optimal policy to maximize the average of all agents' local returns. Due to the non-concave performance function of policy gradient, the existing distributed stochastic optimization methods for convex problems cannot be directly used for policy gradient in MARL. This paper proposes a distributed policy gradient with variance reduction and gradient tracking to address the high variances of policy gradient, and utilizes importance weight to solve the non-stationary problem in the sampling process. We then provide an upper bound on the mean-squared stationary gap, which depends on the number of iterations, the mini-batch size, the epoch size, the problem parameters, and the network topology. We further establish the sample and communication complexity to obtain an $\epsilon$-approximate stationary point. Numerical experiments on the control problem in MARL are performed to validate the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge