Large receptive field strategy and important feature extraction strategy in 3D object detection

The enhancement of 3D object detection is pivotal for precise environmental perception and improved task execution capabilities in autonomous driving. LiDAR point clouds, offering accurate depth information, serve as a crucial information for this purpose. Our study focuses on key challenges in 3D target detection. To tackle the challenge of expanding the receptive field of a 3D convolutional kernel, we introduce the Dynamic Feature Fusion Module (DFFM). This module achieves adaptive expansion of the 3D convolutional kernel's receptive field, balancing the expansion with acceptable computational loads. This innovation reduces operations, expands the receptive field, and allows the model to dynamically adjust to different object requirements. Simultaneously, we identify redundant information in 3D features. Employing the Feature Selection Module (FSM) quantitatively evaluates and eliminates non-important features, achieving the separation of output box fitting and feature extraction. This innovation enables the detector to focus on critical features, resulting in model compression, reduced computational burden, and minimized candidate frame interference. Extensive experiments confirm that both DFFM and FSM not only enhance current benchmarks, particularly in small target detection, but also accelerate network performance. Importantly, these modules exhibit effective complementarity.

Distributed Online Convex Optimization with Adversarial Constraints: Reduced Cumulative Constraint Violation Bounds under Slater's Condition

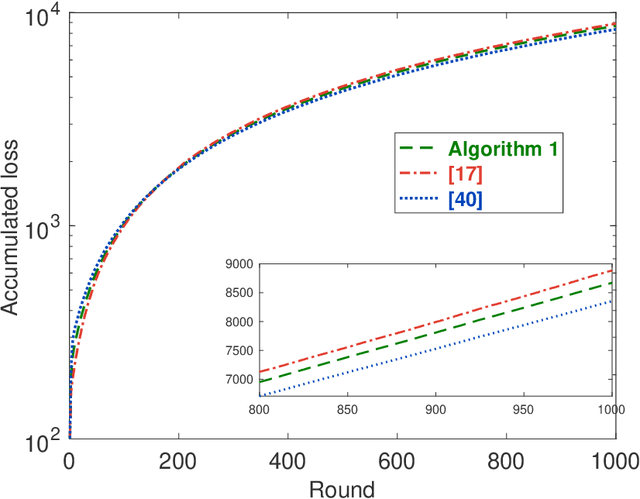
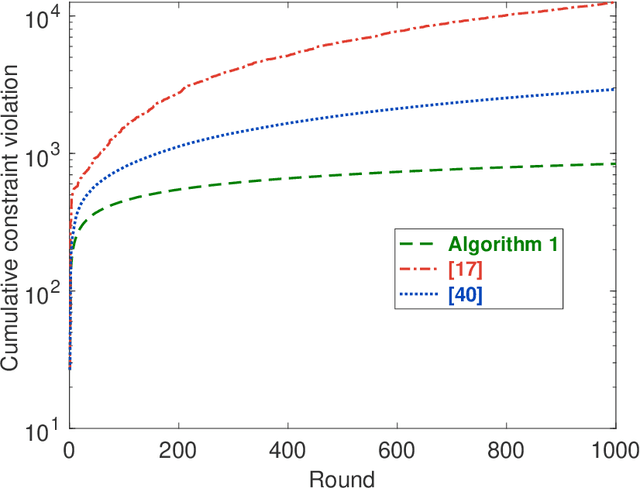
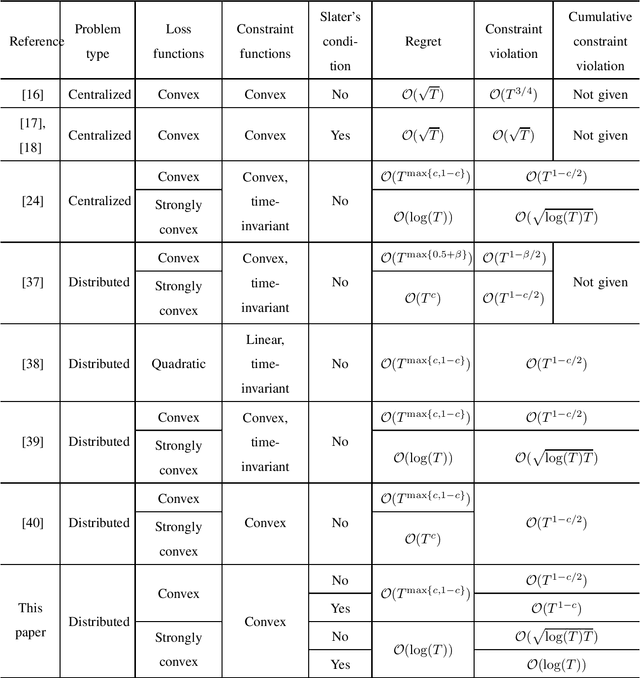
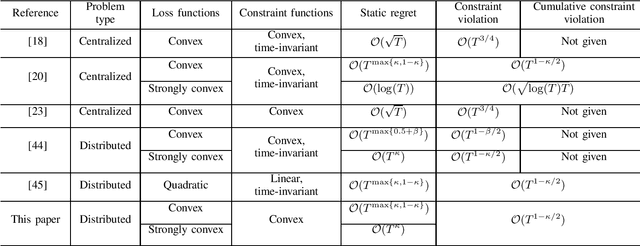
This paper considers distributed online convex optimization with adversarial constraints. In this setting, a network of agents makes decisions at each round, and then only a portion of the loss function and a coordinate block of the constraint function are privately revealed to each agent. The loss and constraint functions are convex and can vary arbitrarily across rounds. The agents collaborate to minimize network regret and cumulative constraint violation. A novel distributed online algorithm is proposed and it achieves an $\mathcal{O}(T^{\max\{c,1-c\}})$ network regret bound and an $\mathcal{O}(T^{1-c/2})$ network cumulative constraint violation bound, where $T$ is the number of rounds and $c\in(0,1)$ is a user-defined trade-off parameter. When Slater's condition holds (i.e, there is a point that strictly satisfies the inequality constraints), the network cumulative constraint violation bound is reduced to $\mathcal{O}(T^{1-c})$. Moreover, if the loss functions are strongly convex, then the network regret bound is reduced to $\mathcal{O}(\log(T))$, and the network cumulative constraint violation bound is reduced to $\mathcal{O}(\sqrt{\log(T)T})$ and $\mathcal{O}(\log(T))$ without and with Slater's condition, respectively. To the best of our knowledge, this paper is the first to achieve reduced (network) cumulative constraint violation bounds for (distributed) online convex optimization with adversarial constraints under Slater's condition. Finally, the theoretical results are verified through numerical simulations.

A Generalized Multi-Modal Fusion Detection Framework

LiDAR point clouds have become the most common data source in autonomous driving. However, due to the sparsity of point clouds, accurate and reliable detection cannot be achieved in specific scenarios. Because of their complementarity with point clouds, images are getting increasing attention. Although with some success, existing fusion methods either perform hard fusion or do not fuse in a direct manner. In this paper, we propose a generic 3D detection framework called MMFusion, using multi-modal features. The framework aims to achieve accurate fusion between LiDAR and images to improve 3D detection in complex scenes. Our framework consists of two separate streams: the LiDAR stream and the camera stream, which can be compatible with any single-modal feature extraction network. The Voxel Local Perception Module in the LiDAR stream enhances local feature representation, and then the Multi-modal Feature Fusion Module selectively combines feature output from different streams to achieve better fusion. Extensive experiments have shown that our framework not only outperforms existing benchmarks but also improves their detection, especially for detecting cyclists and pedestrians on KITTI benchmarks, with strong robustness and generalization capabilities. Hopefully, our work will stimulate more research into multi-modal fusion for autonomous driving tasks.

A Survey of Decision Making in Adversarial Games

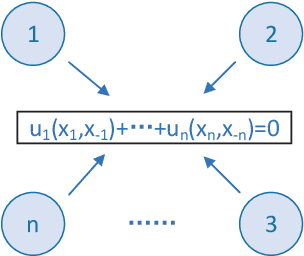
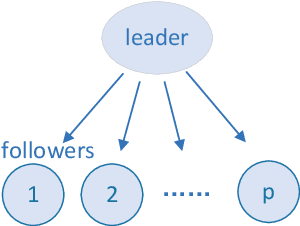
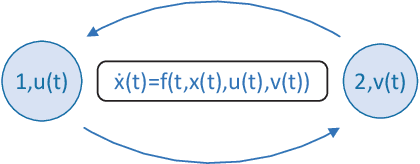
Game theory has by now found numerous applications in various fields, including economics, industry, jurisprudence, and artificial intelligence, where each player only cares about its own interest in a noncooperative or cooperative manner, but without obvious malice to other players. However, in many practical applications, such as poker, chess, evader pursuing, drug interdiction, coast guard, cyber-security, and national defense, players often have apparently adversarial stances, that is, selfish actions of each player inevitably or intentionally inflict loss or wreak havoc on other players. Along this line, this paper provides a systematic survey on three main game models widely employed in adversarial games, i.e., zero-sum normal-form and extensive-form games, Stackelberg (security) games, zero-sum differential games, from an array of perspectives, including basic knowledge of game models, (approximate) equilibrium concepts, problem classifications, research frontiers, (approximate) optimal strategy seeking techniques, prevailing algorithms, and practical applications. Finally, promising future research directions are also discussed for relevant adversarial games.

A Survey of Decentralized Online Learning

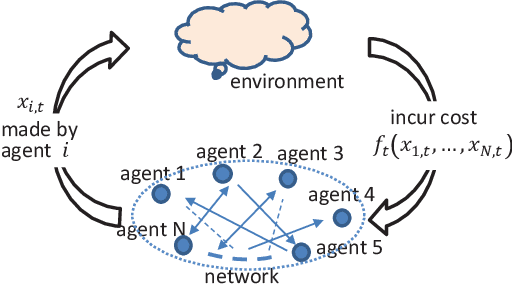
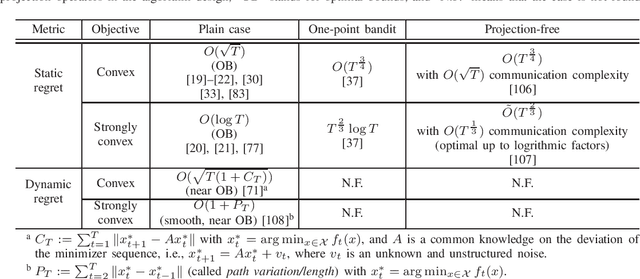
Decentralized online learning (DOL) has been increasingly researched in the last decade, mostly motivated by its wide applications in sensor networks, commercial buildings, robotics (e.g., decentralized target tracking and formation control), smart grids, deep learning, and so forth. In this problem, there are a network of agents who may be cooperative (i.e., decentralized online optimization) or noncooperative (i.e., online game) through local information exchanges, and the local cost function of each agent is often time-varying in dynamic and even adversarial environments. At each time, a decision must be made by each agent based on historical information at hand without knowing future information on cost functions. Although this problem has been extensively studied in the last decade, a comprehensive survey is lacking. Therefore, this paper provides a thorough overview of DOL from the perspective of problem settings, communication, computation, and performances. In addition, some potential future directions are also discussed in details.

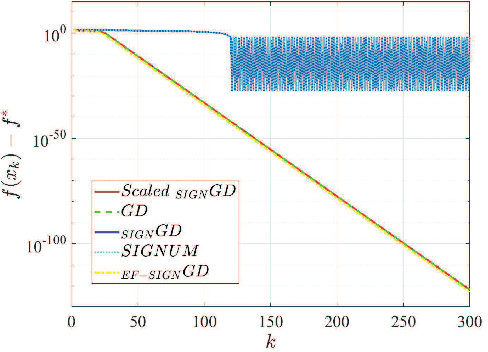
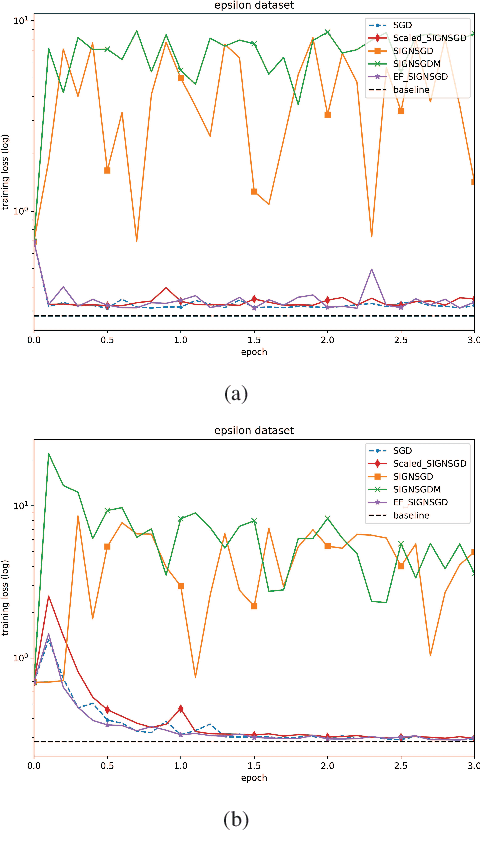
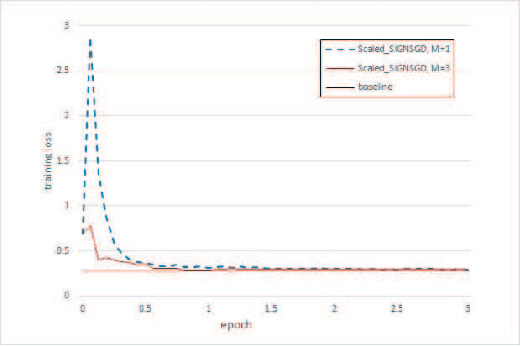
On Faster Convergence of Scaled Sign Gradient Descent

Communication has been seen as a significant bottleneck in industrial applications over large-scale networks. To alleviate the communication burden, sign-based optimization algorithms have gained popularity recently in both industrial and academic communities, which is shown to be closely related to adaptive gradient methods, such as Adam. Along this line, this paper investigates faster convergence for a variant of sign-based gradient descent, called scaled signGD, in three cases: 1) the objective function is strongly convex; 2) the objective function is nonconvex but satisfies the Polyak-Lojasiewicz (PL) inequality; 3) the gradient is stochastic, called scaled signGD in this case. For the first two cases, it can be shown that the scaled signGD converges at a linear rate. For case 3), the algorithm is shown to converge linearly to a neighborhood of the optimal value when a constant learning rate is employed, and the algorithm converges at a rate of $O(1/k)$ when using a diminishing learning rate, where $k$ is the iteration number. The results are also extended to the distributed setting by majority vote in a parameter-server framework. Finally, numerical experiments on logistic regression are performed to corroborate the theoretical findings.

Composition and Application of Current Advanced Driving Assistance System: A Review

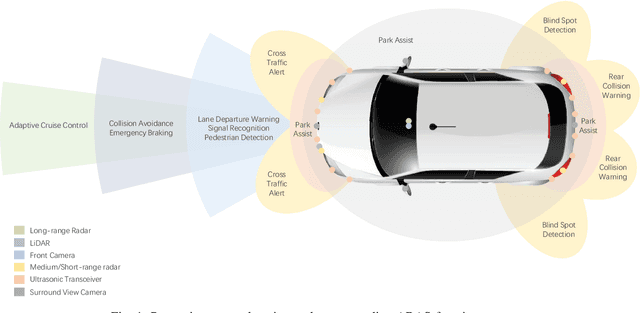
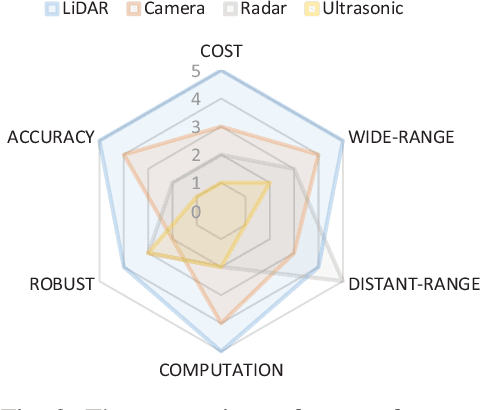
Due to the growing awareness of driving safety and the development of sophisticated technologies, advanced driving assistance system (ADAS) has been equipped in more and more vehicles with higher accuracy and lower price. The latest progress in this field has called for a review to sum up the conventional knowledge of ADAS, the state-of-the-art researches, and novel applications in real-world. With the help of this kind of review, newcomers in this field can get basic knowledge easier and other researchers may be inspired with potential future development possibility. This paper makes a general introduction about ADAS by analyzing its hardware support and computation algorithms. Different types of perception sensors are introduced from their interior feature classifications, installation positions, supporting ADAS functions, and pros and cons. The comparisons between different sensors are concluded and illustrated from their inherent characters and specific usages serving for each ADAS function. The current algorithms for ADAS functions are also collected and briefly presented in this paper from both traditional methods and novel ideas. Additionally, discussions about the definition of ADAS from different institutes are reviewed in this paper, and future approaches about ADAS in China are introduced in particular.

Regret and Cumulative Constraint Violation Analysis for Online Convex Optimization with Long Term Constraints

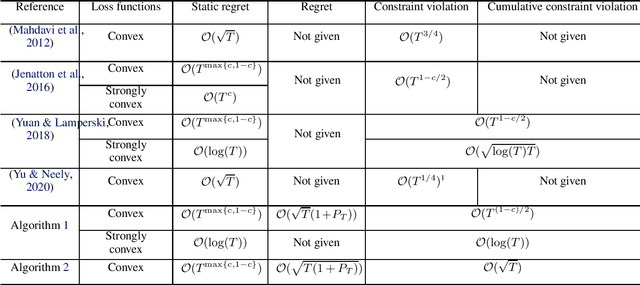
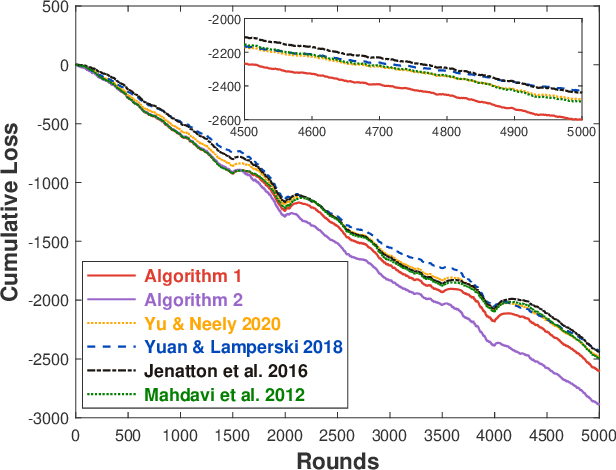
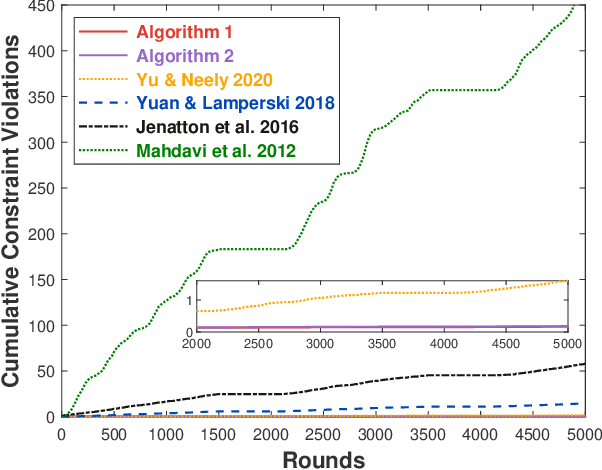
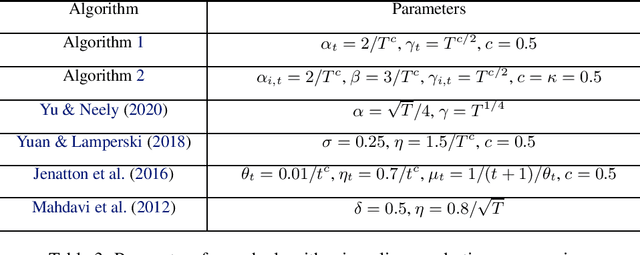
This paper considers online convex optimization with long term constraints, where constraints can be violated in intermediate rounds, but need to be satisfied in the long run. The cumulative constraint violation is used as the metric to measure constraint violations, which excludes the situation that strictly feasible constraints can compensate the effects of violated constraints. A novel algorithm is first proposed and it achieves an $\mathcal{O}(T^{\max\{c,1-c\}})$ bound for static regret and an $\mathcal{O}(T^{(1-c)/2})$ bound for cumulative constraint violation, where $c\in(0,1)$ is a user-defined trade-off parameter, and thus has improved performance compared with existing results. Both static regret and cumulative constraint violation bounds are reduced to $\mathcal{O}(\log(T))$ when the loss functions are strongly convex, which also improves existing results. %In order to bound the regret with respect to any comparator sequence, In order to achieve the optimal regret with respect to any comparator sequence, another algorithm is then proposed and it achieves the optimal $\mathcal{O}(\sqrt{T(1+P_T)})$ regret and an $\mathcal{O}(\sqrt{T})$ cumulative constraint violation, where $P_T$ is the path-length of the comparator sequence. Finally, numerical simulations are provided to illustrate the effectiveness of the theoretical results.

Regret and Cumulative Constraint Violation Analysis for Distributed Online Constrained Convex Optimization

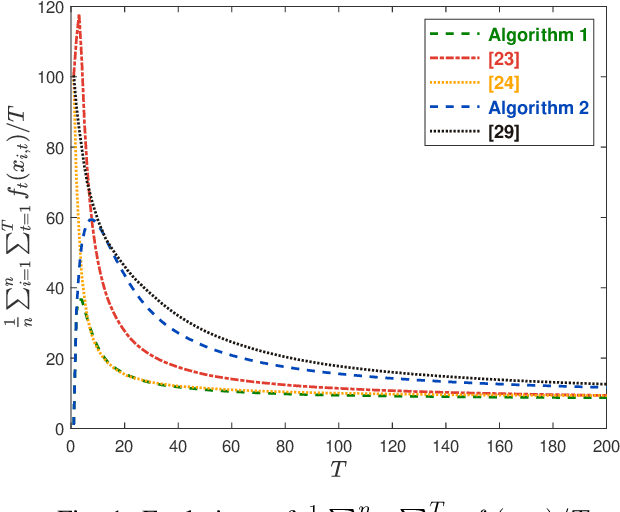
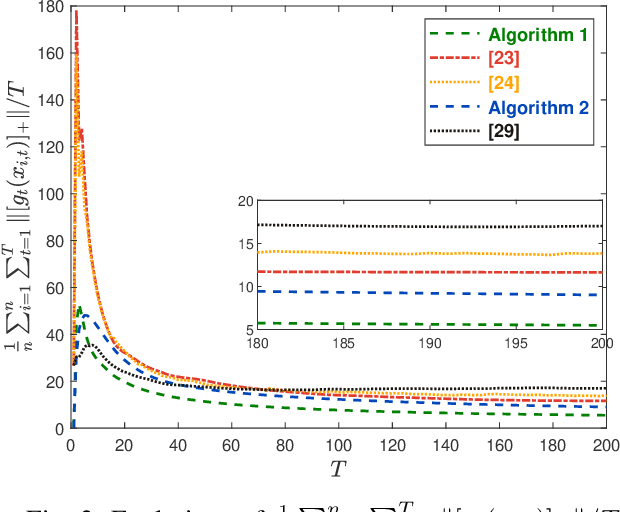
This paper considers the distributed online convex optimization problem with time-varying constraints over a network of agents. This is a sequential decision making problem with two sequences of arbitrarily varying convex loss and constraint functions. At each round, each agent selects a decision from the decision set, and then only a portion of the loss function and a coordinate block of the constraint function at this round are privately revealed to this agent. The goal of the network is to minimize network regret and constraint violation. Two distributed online algorithms with full-information and bandit feedback are proposed. Both dynamic and static network regret bounds are analyzed for the proposed algorithms, and network cumulative constraint violation is used to measure constraint violation, which excludes the situation that strictly feasible constraints can compensate the effects of violated constraints. In particular, we show that the proposed algorithms achieve $\mathcal{O}(T^{\max\{\kappa,1-\kappa\}})$ static network regret and $\mathcal{O}(T^{1-\kappa/2})$ network cumulative constraint violation, where $T$ is the total number of rounds and $\kappa\in(0,1)$ is a user-defined trade-off parameter. Moreover, if the loss functions are strongly convex, then the static network regret bound can be reduced to $\mathcal{O}(T^{\kappa})$. Finally, numerical simulations are provided to illustrate the effectiveness of the theoretical results.

Distributed Online Convex Optimization with Time-Varying Coupled Inequality Constraints

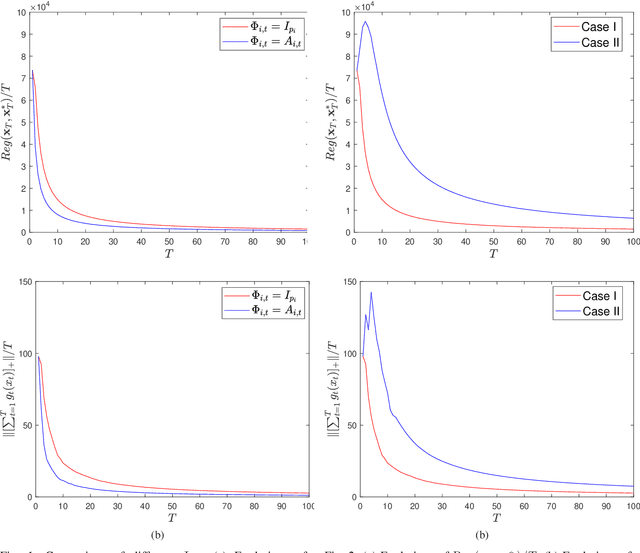
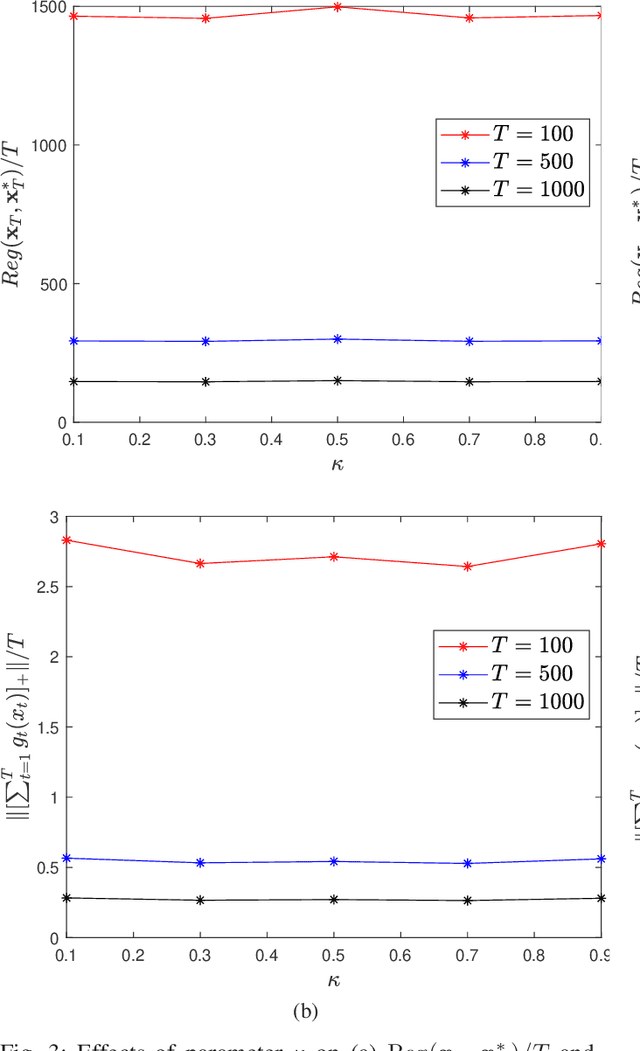
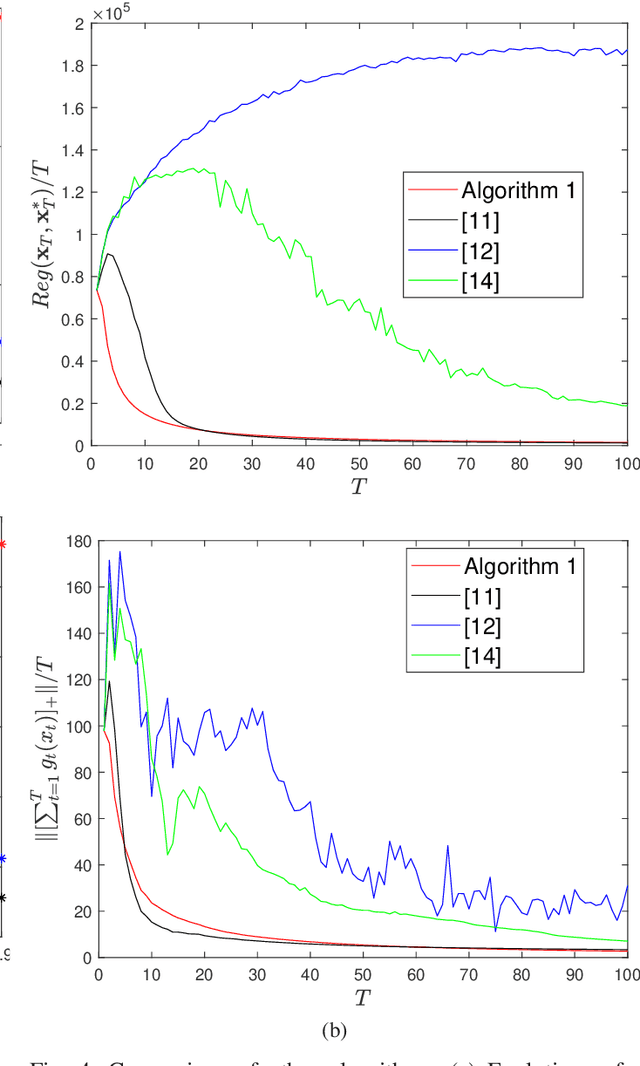
This paper considers distributed online optimization with time-varying coupled inequality constraints. The global objective function is composed of local convex cost and regularization functions and the coupled constraint function is the sum of local convex constraint functions. A distributed online primal-dual dynamic mirror descent algorithm is proposed to solve this problem, where the local cost, regularization, and constraint functions are held privately and revealed only after each time slot. We first derive regret and cumulative constraint violation bounds for the algorithm and show how they depend on the stepsize sequences, the accumulated dynamic variation of the comparator sequence, the number of agents, and the network connectivity. As a result, under some natural decreasing stepsize sequences, we prove that the algorithm achieves sublinear dynamic regret and cumulative constraint violation if the accumulated dynamic variation of the optimal sequence also grows sublinearly. We also prove that the algorithm achieves sublinear static regret and cumulative constraint violation under mild conditions. In addition, smaller bounds on the static regret are achieved when the objective functions are strongly convex. Finally, numerical simulations are provided to illustrate the effectiveness of the theoretical results.