OmniForce: On Human-Centered, Large Model Empowered and Cloud-Edge Collaborative AutoML System

Automated machine learning (AutoML) seeks to build ML models with minimal human effort. While considerable research has been conducted in the area of AutoML in general, aiming to take humans out of the loop when building artificial intelligence (AI) applications, scant literature has focused on how AutoML works well in open-environment scenarios such as the process of training and updating large models, industrial supply chains or the industrial metaverse, where people often face open-loop problems during the search process: they must continuously collect data, update data and models, satisfy the requirements of the development and deployment environment, support massive devices, modify evaluation metrics, etc. Addressing the open-environment issue with pure data-driven approaches requires considerable data, computing resources, and effort from dedicated data engineers, making current AutoML systems and platforms inefficient and computationally intractable. Human-computer interaction is a practical and feasible way to tackle the problem of open-environment AI. In this paper, we introduce OmniForce, a human-centered AutoML (HAML) system that yields both human-assisted ML and ML-assisted human techniques, to put an AutoML system into practice and build adaptive AI in open-environment scenarios. Specifically, we present OmniForce in terms of ML version management; pipeline-driven development and deployment collaborations; a flexible search strategy framework; and widely provisioned and crowdsourced application algorithms, including large models. Furthermore, the (large) models constructed by OmniForce can be automatically turned into remote services in a few minutes; this process is dubbed model as a service (MaaS). Experimental results obtained in multiple search spaces and real-world use cases demonstrate the efficacy and efficiency of OmniForce.

Global Nash Equilibrium in Non-convex Multi-player Game: Theory and Algorithms

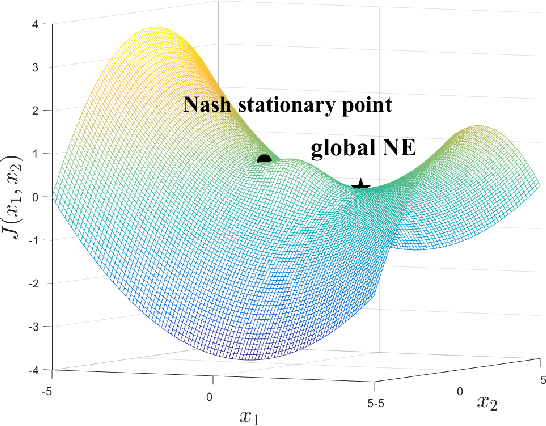
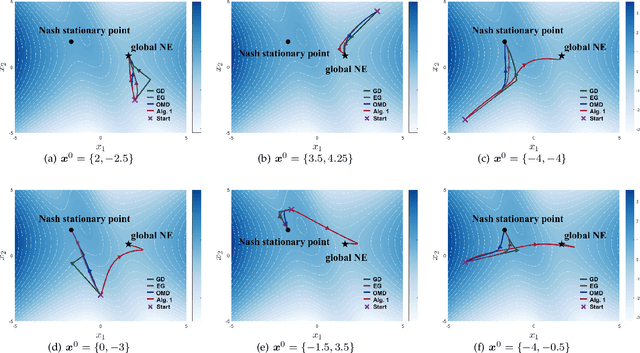
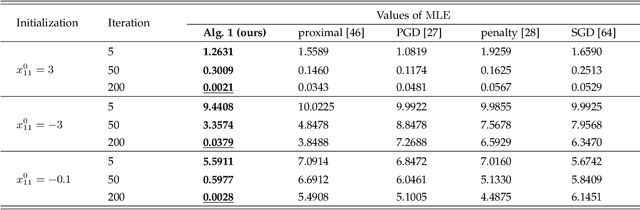
Wide machine learning tasks can be formulated as non-convex multi-player games, where Nash equilibrium (NE) is an acceptable solution to all players, since no one can benefit from changing its strategy unilaterally. Attributed to the non-convexity, obtaining the existence condition of global NE is challenging, let alone designing theoretically guaranteed realization algorithms. This paper takes conjugate transformation to the formulation of non-convex multi-player games, and casts the complementary problem into a variational inequality (VI) problem with a continuous pseudo-gradient mapping. We then prove the existence condition of global NE: the solution to the VI problem satisfies a duality relation. Based on this VI formulation, we design a conjugate-based ordinary differential equation (ODE) to approach global NE, which is proved to have an exponential convergence rate. To make the dynamics more implementable, we further derive a discretized algorithm. We apply our algorithm to two typical scenarios: multi-player generalized monotone game and multi-player potential game. In the two settings, we prove that the step-size setting is required to be $\mathcal{O}(1/k)$ and $\mathcal{O}(1/\sqrt k)$ to yield the convergence rates of $\mathcal{O}(1/ k)$ and $\mathcal{O}(1/\sqrt k)$, respectively. Extensive experiments in robust neural network training and sensor localization are in full agreement with our theory.