Bridging Molecular Graphs and Large Language Models

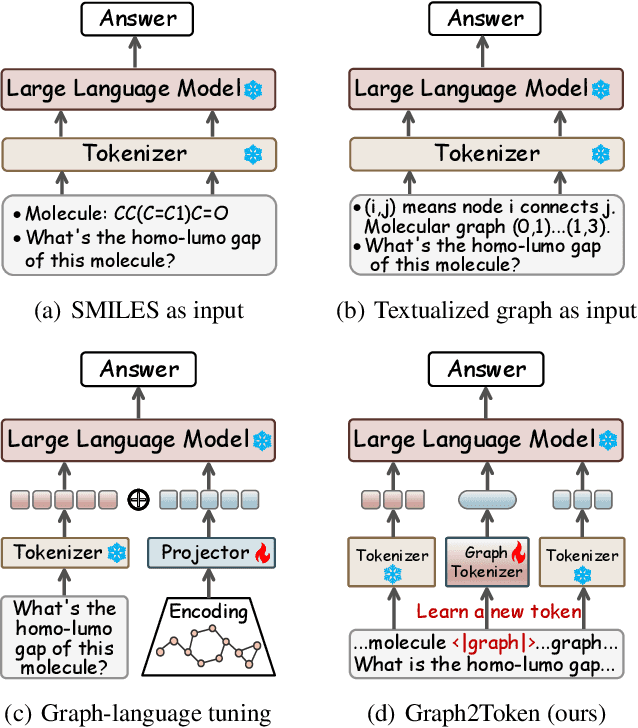
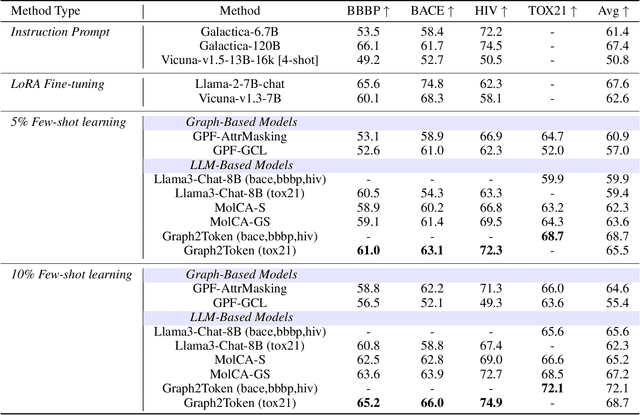
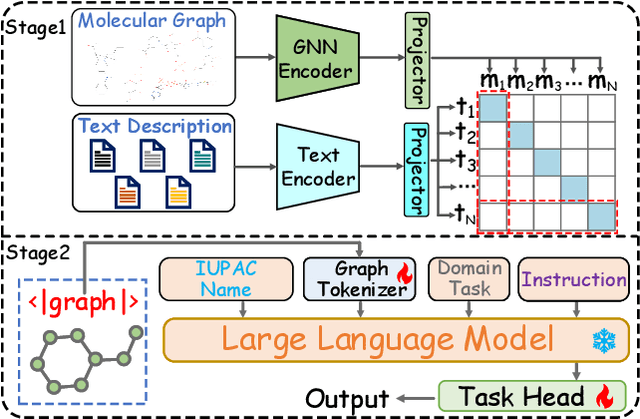
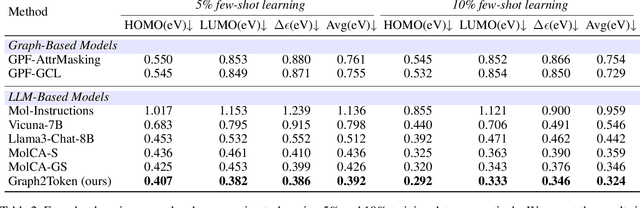
While Large Language Models (LLMs) have shown exceptional generalization capabilities, their ability to process graph data, such as molecular structures, remains limited. To bridge this gap, this paper proposes Graph2Token, an efficient solution that aligns graph tokens to LLM tokens. The key idea is to represent a graph token with the LLM token vocabulary, without fine-tuning the LLM backbone. To achieve this goal, we first construct a molecule-text paired dataset from multisources, including CHEBI and HMDB, to train a graph structure encoder, which reduces the distance between graphs and texts representations in the feature space. Then, we propose a novel alignment strategy that associates a graph token with LLM tokens. To further unleash the potential of LLMs, we collect molecular IUPAC name identifiers, which are incorporated into the LLM prompts. By aligning molecular graphs as special tokens, we can activate LLM generalization ability to molecular few-shot learning. Extensive experiments on molecular classification and regression tasks demonstrate the effectiveness of our proposed Graph2Token.

Topology-Driven Attribute Recovery for Attribute Missing Graph Learning in Social Internet of Things

With the advancement of information technology, the Social Internet of Things (SIoT) has fostered the integration of physical devices and social networks, deepening the study of complex interaction patterns. Text Attribute Graphs (TAGs) capture both topological structures and semantic attributes, enhancing the analysis of complex interactions within the SIoT. However, existing graph learning methods are typically designed for complete attributed graphs, and the common issue of missing attributes in Attribute Missing Graphs (AMGs) increases the difficulty of analysis tasks. To address this, we propose the Topology-Driven Attribute Recovery (TDAR) framework, which leverages topological data for AMG learning. TDAR introduces an improved pre-filling method for initial attribute recovery using native graph topology. Additionally, it dynamically adjusts propagation weights and incorporates homogeneity strategies within the embedding space to suit AMGs' unique topological structures, effectively reducing noise during information propagation. Extensive experiments on public datasets demonstrate that TDAR significantly outperforms state-of-the-art methods in attribute reconstruction and downstream tasks, offering a robust solution to the challenges posed by AMGs. The code is available at https://github.com/limengran98/TDAR.

Graph2text or Graph2token: A Perspective of Large Language Models for Graph Learning

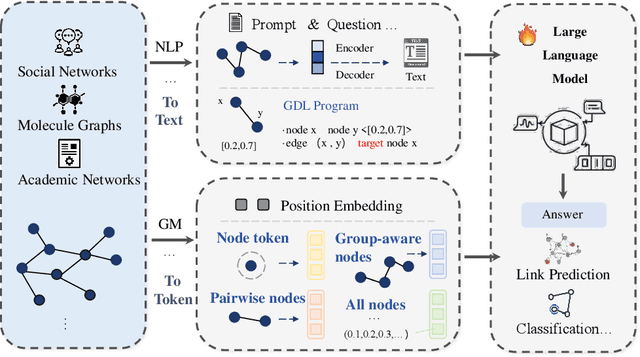
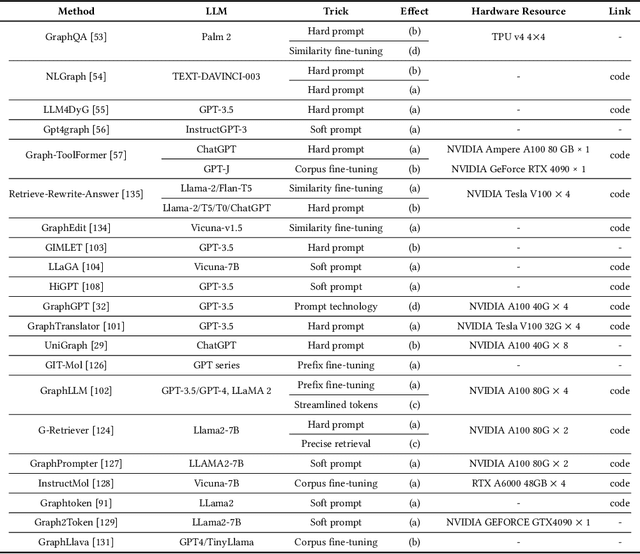
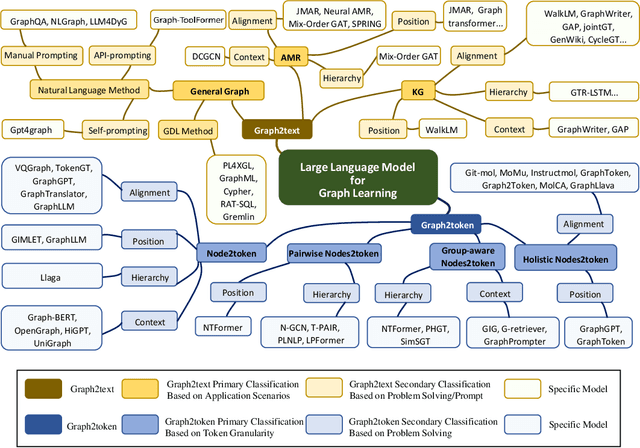
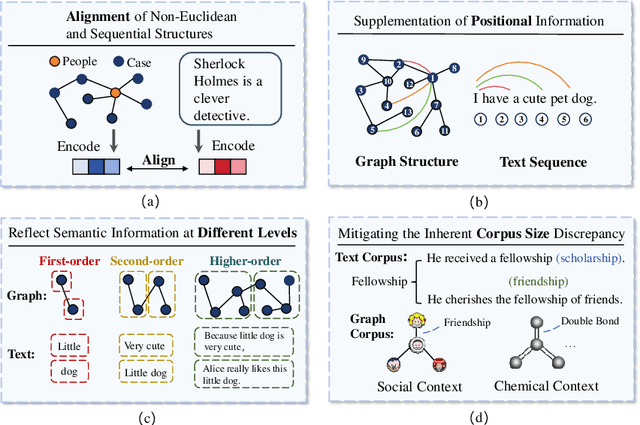
Graphs are data structures used to represent irregular networks and are prevalent in numerous real-world applications. Previous methods directly model graph structures and achieve significant success. However, these methods encounter bottlenecks due to the inherent irregularity of graphs. An innovative solution is converting graphs into textual representations, thereby harnessing the powerful capabilities of Large Language Models (LLMs) to process and comprehend graphs. In this paper, we present a comprehensive review of methodologies for applying LLMs to graphs, termed LLM4graph. The core of LLM4graph lies in transforming graphs into texts for LLMs to understand and analyze. Thus, we propose a novel taxonomy of LLM4graph methods in the view of the transformation. Specifically, existing methods can be divided into two paradigms: Graph2text and Graph2token, which transform graphs into texts or tokens as the input of LLMs, respectively. We point out four challenges during the transformation to systematically present existing methods in a problem-oriented perspective. For practical concerns, we provide a guideline for researchers on selecting appropriate models and LLMs for different graphs and hardware constraints. We also identify five future research directions for LLM4graph.

Generalizing Knowledge Graph Embedding with Universal Orthogonal Parameterization

Recent advances in knowledge graph embedding (KGE) rely on Euclidean/hyperbolic orthogonal relation transformations to model intrinsic logical patterns and topological structures. However, existing approaches are confined to rigid relational orthogonalization with restricted dimension and homogeneous geometry, leading to deficient modeling capability. In this work, we move beyond these approaches in terms of both dimension and geometry by introducing a powerful framework named GoldE, which features a universal orthogonal parameterization based on a generalized form of Householder reflection. Such parameterization can naturally achieve dimensional extension and geometric unification with theoretical guarantees, enabling our framework to simultaneously capture crucial logical patterns and inherent topological heterogeneity of knowledge graphs. Empirically, GoldE achieves state-of-the-art performance on three standard benchmarks. Codes are available at https://github.com/xxrep/GoldE.

How Can Large Language Models Understand Spatial-Temporal Data?

While Large Language Models (LLMs) dominate tasks like natural language processing and computer vision, harnessing their power for spatial-temporal forecasting remains challenging. The disparity between sequential text and complex spatial-temporal data hinders this application. To address this issue, this paper introduces STG-LLM, an innovative approach empowering LLMs for spatial-temporal forecasting. We tackle the data mismatch by proposing: 1) STG-Tokenizer: This spatial-temporal graph tokenizer transforms intricate graph data into concise tokens capturing both spatial and temporal relationships; 2) STG-Adapter: This minimalistic adapter, consisting of linear encoding and decoding layers, bridges the gap between tokenized data and LLM comprehension. By fine-tuning only a small set of parameters, it can effectively grasp the semantics of tokens generated by STG-Tokenizer, while preserving the original natural language understanding capabilities of LLMs. Extensive experiments on diverse spatial-temporal benchmark datasets show that STG-LLM successfully unlocks LLM potential for spatial-temporal forecasting. Remarkably, our approach achieves competitive performance on par with dedicated SOTA methods.

To Copy Rather Than Memorize: A Vertical Learning Paradigm for Knowledge Graph Completion

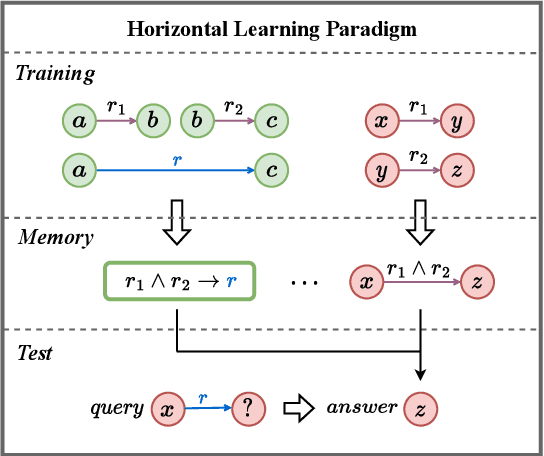
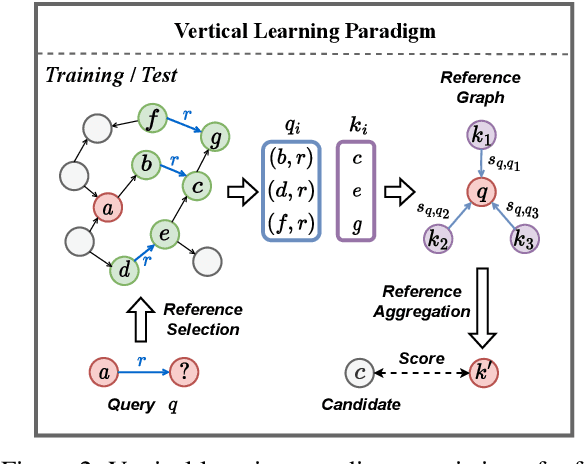
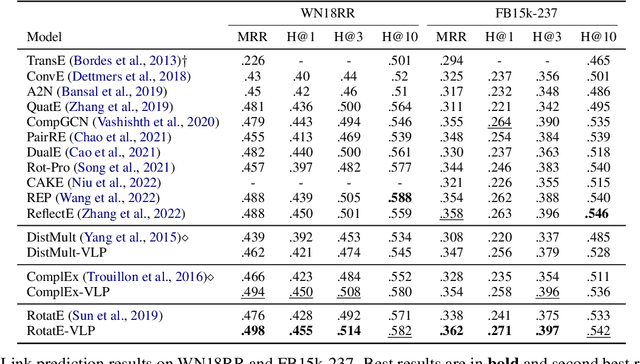
Embedding models have shown great power in knowledge graph completion (KGC) task. By learning structural constraints for each training triple, these methods implicitly memorize intrinsic relation rules to infer missing links. However, this paper points out that the multi-hop relation rules are hard to be reliably memorized due to the inherent deficiencies of such implicit memorization strategy, making embedding models underperform in predicting links between distant entity pairs. To alleviate this problem, we present Vertical Learning Paradigm (VLP), which extends embedding models by allowing to explicitly copy target information from related factual triples for more accurate prediction. Rather than solely relying on the implicit memory, VLP directly provides additional cues to improve the generalization ability of embedding models, especially making the distant link prediction significantly easier. Moreover, we also propose a novel relative distance based negative sampling technique (ReD) for more effective optimization. Experiments demonstrate the validity and generality of our proposals on two standard benchmarks. Our code is available at https://github.com/rui9812/VLP.

Towards Better Graph Representation Learning with Parameterized Decomposition & Filtering

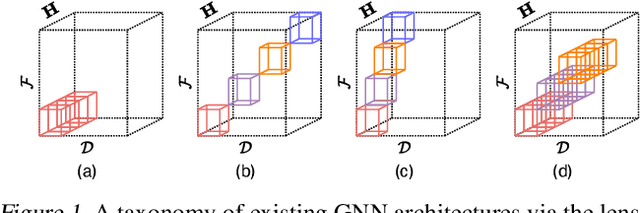
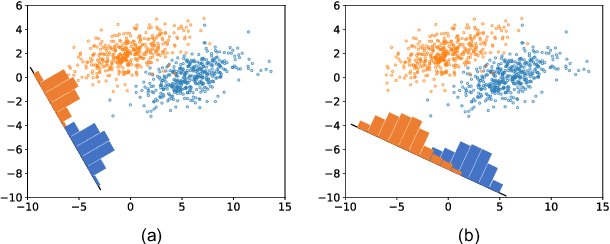
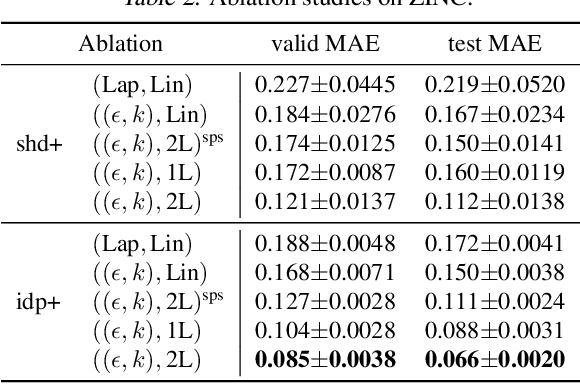
Proposing an effective and flexible matrix to represent a graph is a fundamental challenge that has been explored from multiple perspectives, e.g., filtering in Graph Fourier Transforms. In this work, we develop a novel and general framework which unifies many existing GNN models from the view of parameterized decomposition and filtering, and show how it helps to enhance the flexibility of GNNs while alleviating the smoothness and amplification issues of existing models. Essentially, we show that the extensively studied spectral graph convolutions with learnable polynomial filters are constrained variants of this formulation, and releasing these constraints enables our model to express the desired decomposition and filtering simultaneously. Based on this generalized framework, we develop models that are simple in implementation but achieve significant improvements and computational efficiency on a variety of graph learning tasks. Code is available at https://github.com/qslim/PDF.

NodeTrans: A Graph Transfer Learning Approach for Traffic Prediction

Recently, deep learning methods have made great progress in traffic prediction, but their performance depends on a large amount of historical data. In reality, we may face the data scarcity issue. In this case, deep learning models fail to obtain satisfactory performance. Transfer learning is a promising approach to solve the data scarcity issue. However, existing transfer learning approaches in traffic prediction are mainly based on regular grid data, which is not suitable for the inherent graph data in the traffic network. Moreover, existing graph-based models can only capture shared traffic patterns in the road network, and how to learn node-specific patterns is also a challenge. In this paper, we propose a novel transfer learning approach to solve the traffic prediction with few data, which can transfer the knowledge learned from a data-rich source domain to a data-scarce target domain. First, a spatial-temporal graph neural network is proposed, which can capture the node-specific spatial-temporal traffic patterns of different road networks. Then, to improve the robustness of transfer, we design a pattern-based transfer strategy, where we leverage a clustering-based mechanism to distill common spatial-temporal patterns in the source domain, and use these knowledge to further improve the prediction performance of the target domain. Experiments on real-world datasets verify the effectiveness of our approach.

Soft-mask: Adaptive Substructure Extractions for Graph Neural Networks

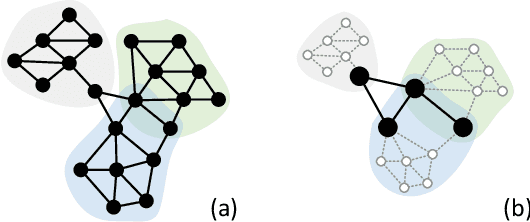
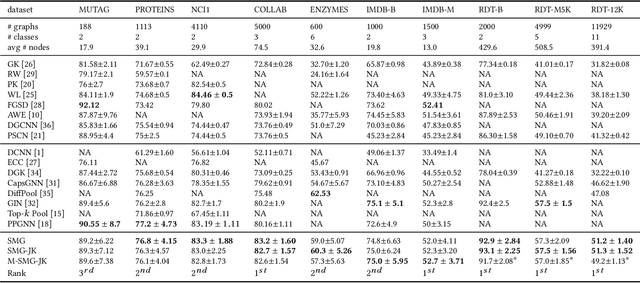
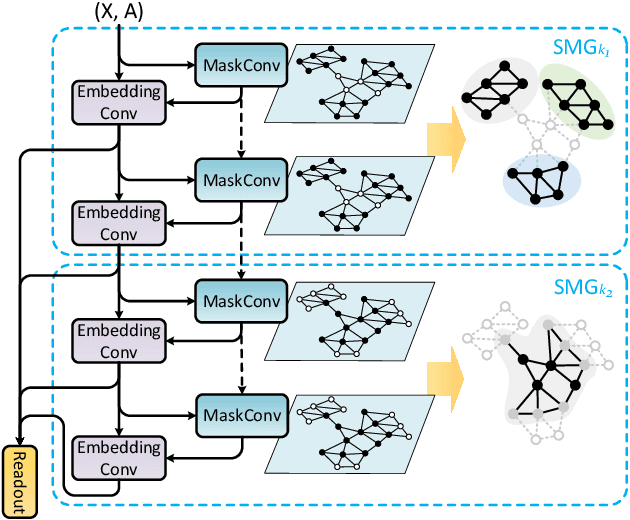
For learning graph representations, not all detailed structures within a graph are relevant to the given graph tasks. Task-relevant structures can be $localized$ or $sparse$ which are only involved in subgraphs or characterized by the interactions of subgraphs (a hierarchical perspective). A graph neural network should be able to efficiently extract task-relevant structures and be invariant to irrelevant parts, which is challenging for general message passing GNNs. In this work, we propose to learn graph representations from a sequence of subgraphs of the original graph to better capture task-relevant substructures or hierarchical structures and skip $noisy$ parts. To this end, we design soft-mask GNN layer to extract desired subgraphs through the mask mechanism. The soft-mask is defined in a continuous space to maintain the differentiability and characterize the weights of different parts. Compared with existing subgraph or hierarchical representation learning methods and graph pooling operations, the soft-mask GNN layer is not limited by the fixed sample or drop ratio, and therefore is more flexible to extract subgraphs with arbitrary sizes. Extensive experiments on public graph benchmarks show that soft-mask mechanism brings performance improvements. And it also provides interpretability where visualizing the values of masks in each layer allows us to have an insight into the structures learned by the model.

HousE: Knowledge Graph Embedding with Householder Parameterization

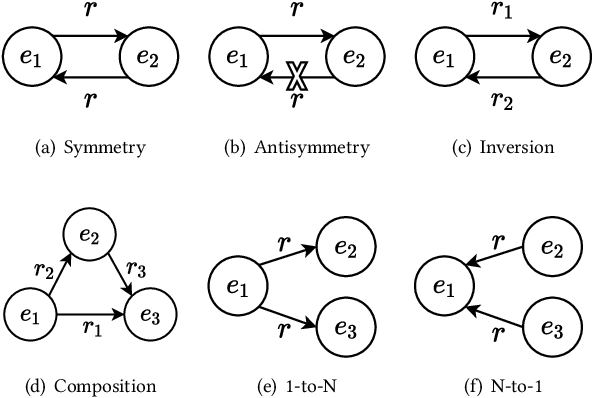
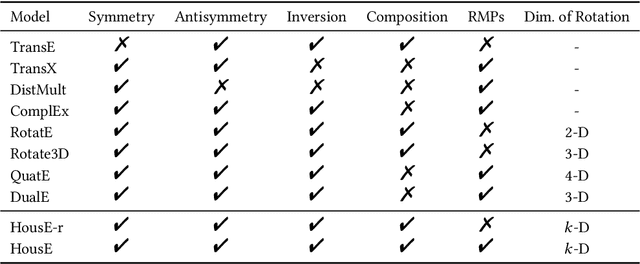
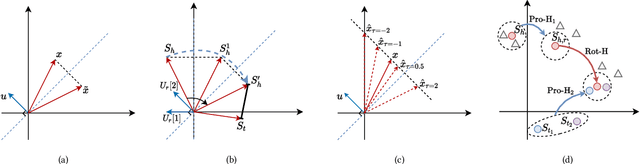
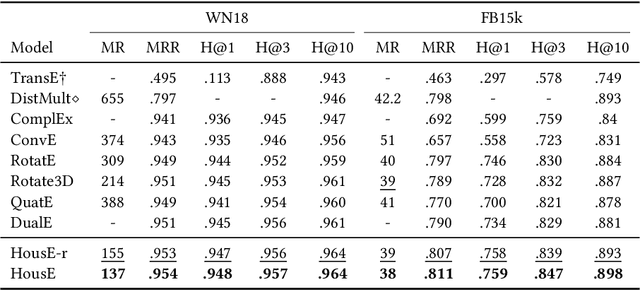
The effectiveness of knowledge graph embedding (KGE) largely depends on the ability to model intrinsic relation patterns and mapping properties. However, existing approaches can only capture some of them with insufficient modeling capacity. In this work, we propose a more powerful KGE framework named HousE, which involves a novel parameterization based on two kinds of Householder transformations: (1) Householder rotations to achieve superior capacity of modeling relation patterns; (2) Householder projections to handle sophisticated relation mapping properties. Theoretically, HousE is capable of modeling crucial relation patterns and mapping properties simultaneously. Besides, HousE is a generalization of existing rotation-based models while extending the rotations to high-dimensional spaces. Empirically, HousE achieves new state-of-the-art performance on five benchmark datasets. Our code is available at https://github.com/anrep/HousE.