Xuyang Chen
MeSS: City Mesh-Guided Outdoor Scene Generation with Cross-View Consistent Diffusion
Aug 21, 2025Abstract:Mesh models have become increasingly accessible for numerous cities; however, the lack of realistic textures restricts their application in virtual urban navigation and autonomous driving. To address this, this paper proposes MeSS (Meshbased Scene Synthesis) for generating high-quality, styleconsistent outdoor scenes with city mesh models serving as the geometric prior. While image and video diffusion models can leverage spatial layouts (such as depth maps or HD maps) as control conditions to generate street-level perspective views, they are not directly applicable to 3D scene generation. Video diffusion models excel at synthesizing consistent view sequences that depict scenes but often struggle to adhere to predefined camera paths or align accurately with rendered control videos. In contrast, image diffusion models, though unable to guarantee cross-view visual consistency, can produce more geometry-aligned results when combined with ControlNet. Building on this insight, our approach enhances image diffusion models by improving cross-view consistency. The pipeline comprises three key stages: first, we generate geometrically consistent sparse views using Cascaded Outpainting ControlNets; second, we propagate denser intermediate views via a component dubbed AGInpaint; and third, we globally eliminate visual inconsistencies (e.g., varying exposure) using the GCAlign module. Concurrently with generation, a 3D Gaussian Splatting (3DGS) scene is reconstructed by initializing Gaussian balls on the mesh surface. Our method outperforms existing approaches in both geometric alignment and generation quality. Once synthesized, the scene can be rendered in diverse styles through relighting and style transfer techniques.
QoE Optimization for Semantic Self-Correcting Video Transmission in Multi-UAV Networks
Jul 09, 2025
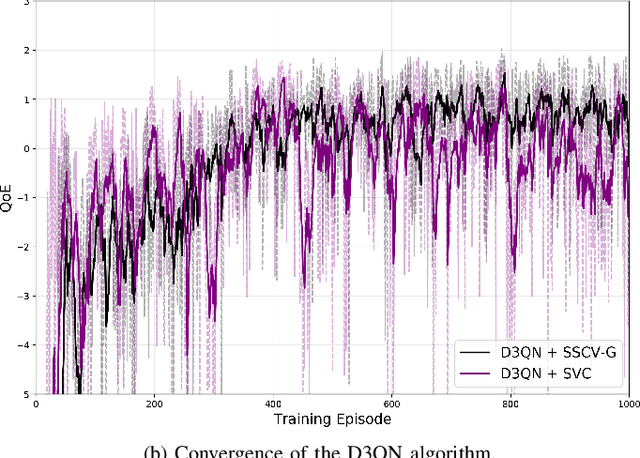
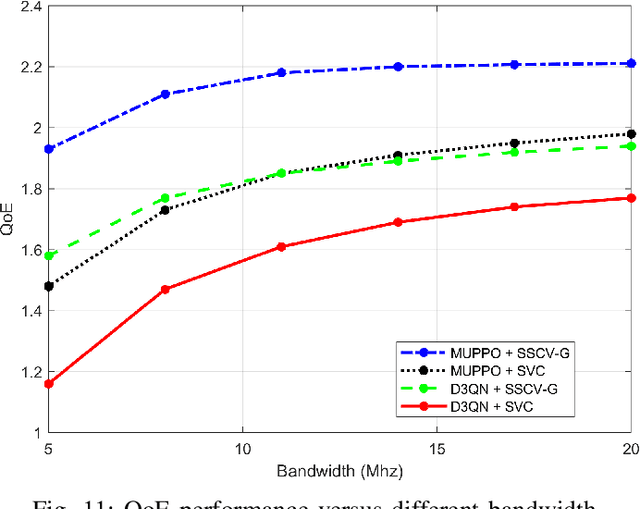
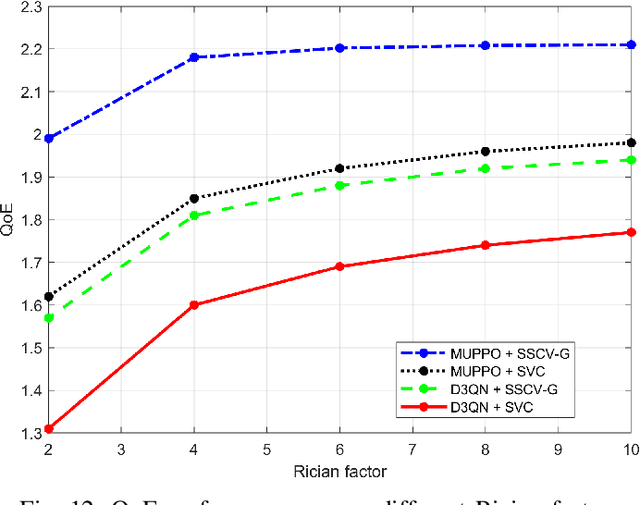
Abstract:Real-time unmanned aerial vehicle (UAV) video streaming is essential for time-sensitive applications, including remote surveillance, emergency response, and environmental monitoring. However, it faces challenges such as limited bandwidth, latency fluctuations, and high packet loss. To address these issues, we propose a novel semantic self-correcting video transmission framework with ultra-fine bitrate granularity (SSCV-G). In SSCV-G, video frames are encoded into a compact semantic codebook space, and the transmitter adaptively sends a subset of semantic indices based on bandwidth availability, enabling fine-grained bitrate control for improved bandwidth efficiency. At the receiver, a spatio-temporal vision transformer (ST-ViT) performs multi-frame joint decoding to reconstruct dropped semantic indices by modeling intra- and inter-frame dependencies. To further improve performance under dynamic network conditions, we integrate a multi-user proximal policy optimization (MUPPO) reinforcement learning scheme that jointly optimizes communication resource allocation and semantic bitrate selection to maximize user Quality of Experience (QoE). Extensive experiments demonstrate that the proposed SSCV-G significantly outperforms state-of-the-art video codecs in coding efficiency, bandwidth adaptability, and packet loss robustness. Moreover, the proposed MUPPO-based QoE optimization consistently surpasses existing benchmarks.
Taming OOD Actions for Offline Reinforcement Learning: An Advantage-Based Approach
May 08, 2025Abstract:Offline reinforcement learning (RL) aims to learn decision-making policies from fixed datasets without online interactions, providing a practical solution where online data collection is expensive or risky. However, offline RL often suffers from distribution shift, resulting in inaccurate evaluation and substantial overestimation on out-of-distribution (OOD) actions. To address this, existing approaches incorporate conservatism by indiscriminately discouraging all OOD actions, thereby hindering the agent's ability to generalize and exploit beneficial ones. In this paper, we propose Advantage-based Diffusion Actor-Critic (ADAC), a novel method that systematically evaluates OOD actions using the batch-optimal value function. Based on this evaluation, ADAC defines an advantage function to modulate the Q-function update, enabling more precise assessment of OOD action quality. We design a custom PointMaze environment and collect datasets to visually reveal that advantage modulation can effectively identify and select superior OOD actions. Extensive experiments show that ADAC achieves state-of-the-art performance on almost all tasks in the D4RL benchmark, with particularly clear margins on the more challenging tasks.
Global Optimality of Single-Timescale Actor-Critic under Continuous State-Action Space: A Study on Linear Quadratic Regulator
May 02, 2025
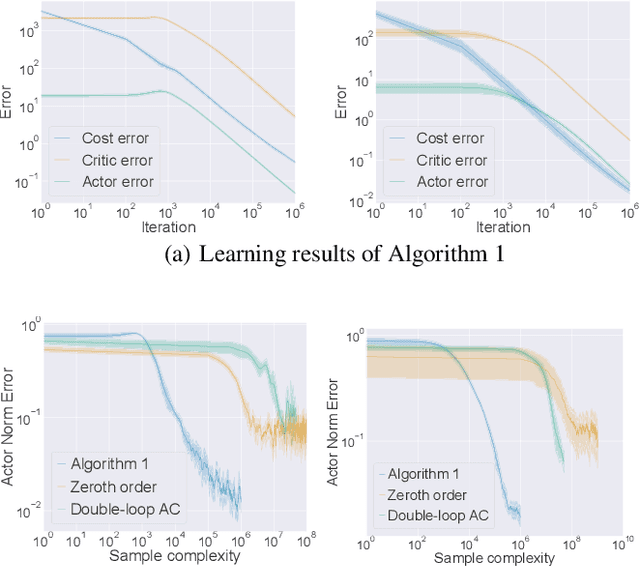
Abstract:Actor-critic methods have achieved state-of-the-art performance in various challenging tasks. However, theoretical understandings of their performance remain elusive and challenging. Existing studies mostly focus on practically uncommon variants such as double-loop or two-timescale stepsize actor-critic algorithms for simplicity. These results certify local convergence on finite state- or action-space only. We push the boundary to investigate the classic single-sample single-timescale actor-critic on continuous (infinite) state-action space, where we employ the canonical linear quadratic regulator (LQR) problem as a case study. We show that the popular single-timescale actor-critic can attain an epsilon-optimal solution with an order of epsilon to -2 sample complexity for solving LQR on the demanding continuous state-action space. Our work provides new insights into the performance of single-timescale actor-critic, which further bridges the gap between theory and practice.
VIPO: Value Function Inconsistency Penalized Offline Reinforcement Learning
Apr 16, 2025Abstract:Offline reinforcement learning (RL) learns effective policies from pre-collected datasets, offering a practical solution for applications where online interactions are risky or costly. Model-based approaches are particularly advantageous for offline RL, owing to their data efficiency and generalizability. However, due to inherent model errors, model-based methods often artificially introduce conservatism guided by heuristic uncertainty estimation, which can be unreliable. In this paper, we introduce VIPO, a novel model-based offline RL algorithm that incorporates self-supervised feedback from value estimation to enhance model training. Specifically, the model is learned by additionally minimizing the inconsistency between the value learned directly from the offline data and the one estimated from the model. We perform comprehensive evaluations from multiple perspectives to show that VIPO can learn a highly accurate model efficiently and consistently outperform existing methods. It offers a general framework that can be readily integrated into existing model-based offline RL algorithms to systematically enhance model accuracy. As a result, VIPO achieves state-of-the-art performance on almost all tasks in both D4RL and NeoRL benchmarks.
The Communication and Computation Trade-off in Wireless Semantic Communications
Apr 14, 2025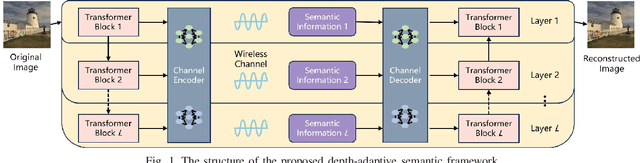
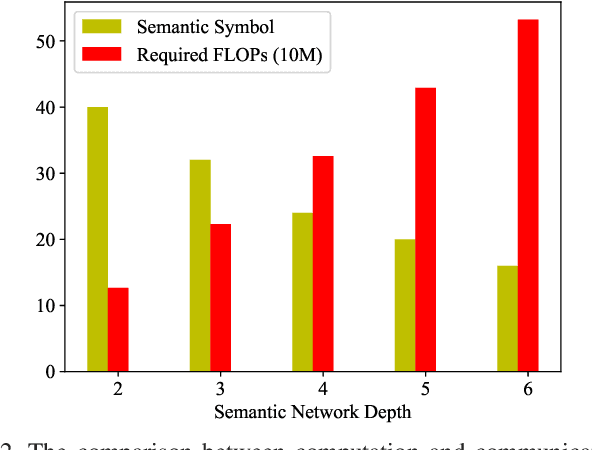
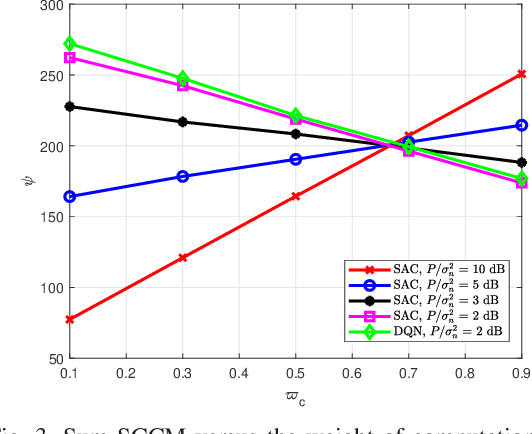
Abstract:Semantic communications have emerged as a crucial research direction for future wireless communication networks. However, as wireless systems become increasingly complex, the demands for computation and communication resources in semantic communications continue to grow rapidly. This paper investigates the trade-off between computation and communication in wireless semantic communications, taking into consideration transmission task delay and performance constraints within the semantic communication framework. We propose a novel tradeoff metric to analyze the balance between computation and communication in semantic transmissions and employ the deep reinforcement learning (DRL) algorithm to minimize this metric, thereby reducing the cost associated with balancing computation and communication. Through simulations, we analyze the tradeoff between computation and communication and demonstrate the effectiveness of optimizing this trade-off metric.
Preference-Guided Reinforcement Learning for Efficient Exploration
Jul 09, 2024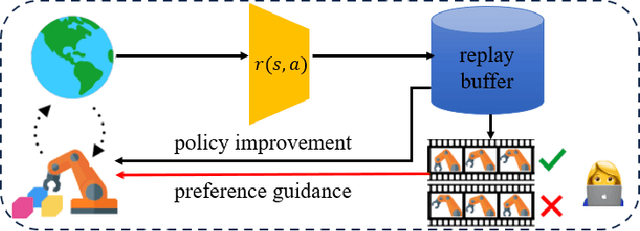
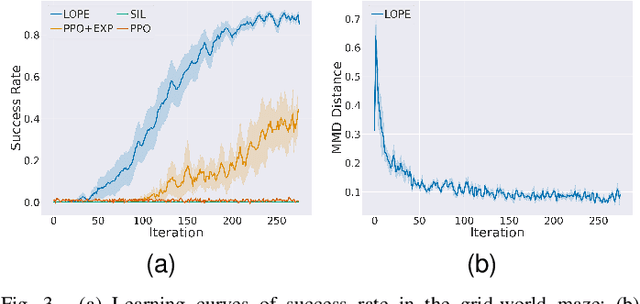
Abstract:In this paper, we investigate preference-based reinforcement learning (PbRL) that allows reinforcement learning (RL) agents to learn from human feedback. This is particularly valuable when defining a fine-grain reward function is not feasible. However, this approach is inefficient and impractical for promoting deep exploration in hard-exploration tasks with long horizons and sparse rewards. To tackle this issue, we introduce LOPE: Learning Online with trajectory Preference guidancE, an end-to-end preference-guided RL framework that enhances exploration efficiency in hard-exploration tasks. Our intuition is that LOPE directly adjusts the focus of online exploration by considering human feedback as guidance, avoiding learning a separate reward model from preferences. Specifically, LOPE includes a two-step sequential policy optimization process consisting of trust-region-based policy improvement and preference guidance steps. We reformulate preference guidance as a novel trajectory-wise state marginal matching problem that minimizes the maximum mean discrepancy distance between the preferred trajectories and the learned policy. Furthermore, we provide a theoretical analysis to characterize the performance improvement bound and evaluate the LOPE's effectiveness. When assessed in various challenging hard-exploration environments, LOPE outperforms several state-of-the-art methods regarding convergence rate and overall performance. The code used in this study is available at \url{https://github.com/buaawgj/LOPE}.
Contrastive Learning of Shared Spatiotemporal EEG Representations Across Individuals for Naturalistic Neuroscience
Feb 22, 2024



Abstract:Neural representations induced by naturalistic stimuli offer insights into how humans respond to peripheral stimuli in daily life. The key to understanding the general neural mechanisms underlying naturalistic stimuli processing involves aligning neural activities across individuals and extracting inter-subject shared neural representations. Targeting the Electroencephalogram (EEG) technique, known for its rich spatial and temporal information, this study presents a general framework for Contrastive Learning of Shared SpatioTemporal EEG Representations across individuals (CL-SSTER). Harnessing the representational capabilities of contrastive learning, CL-SSTER utilizes a neural network to maximize the similarity of EEG representations across individuals for identical stimuli, contrasting with those for varied stimuli. The network employed spatial and temporal convolutions to simultaneously learn the spatial and temporal patterns inherent in EEG. The versatility of CL-SSTER was demonstrated on three EEG datasets, including a synthetic dataset, a speech audio EEG dataset, and an emotional video EEG dataset. CL-SSTER attained the highest inter-subject correlation (ISC) values compared to the state-of-the-art ISC methods. The latent representations generated by CL-SSTER exhibited reliable spatiotemporal EEG patterns, which can be explained by specific aspects of the stimuli. CL-SSTER serves as an interpretable and scalable foundational framework for the identification of inter-subject shared neural representations in the realm of naturalistic neuroscience.
Optimization Landscape of Policy Gradient Methods for Discrete-time Static Output Feedback
Oct 29, 2023
Abstract:In recent times, significant advancements have been made in delving into the optimization landscape of policy gradient methods for achieving optimal control in linear time-invariant (LTI) systems. Compared with state-feedback control, output-feedback control is more prevalent since the underlying state of the system may not be fully observed in many practical settings. This paper analyzes the optimization landscape inherent to policy gradient methods when applied to static output feedback (SOF) control in discrete-time LTI systems subject to quadratic cost. We begin by establishing crucial properties of the SOF cost, encompassing coercivity, L-smoothness, and M-Lipschitz continuous Hessian. Despite the absence of convexity, we leverage these properties to derive novel findings regarding convergence (and nearly dimension-free rate) to stationary points for three policy gradient methods, including the vanilla policy gradient method, the natural policy gradient method, and the Gauss-Newton method. Moreover, we provide proof that the vanilla policy gradient method exhibits linear convergence towards local minima when initialized near such minima. The paper concludes by presenting numerical examples that validate our theoretical findings. These results not only characterize the performance of gradient descent for optimizing the SOF problem but also provide insights into the effectiveness of general policy gradient methods within the realm of reinforcement learning.
Box2Poly: Memory-Efficient Polygon Prediction of Arbitrarily Shaped and Rotated Text
Sep 20, 2023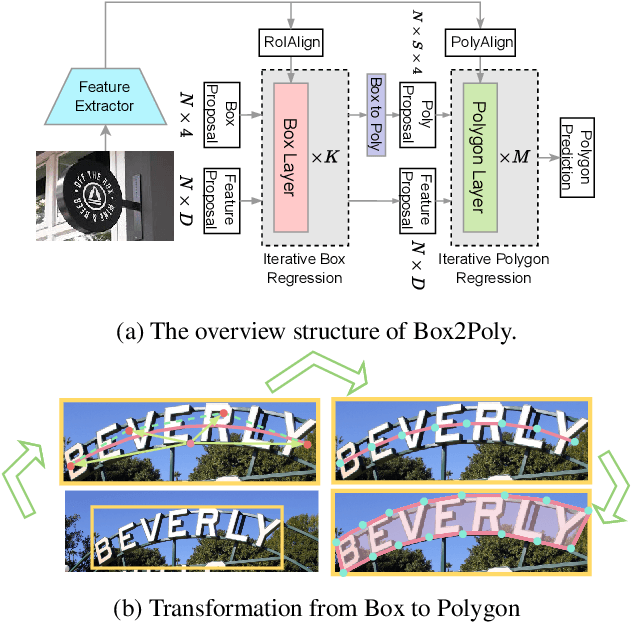

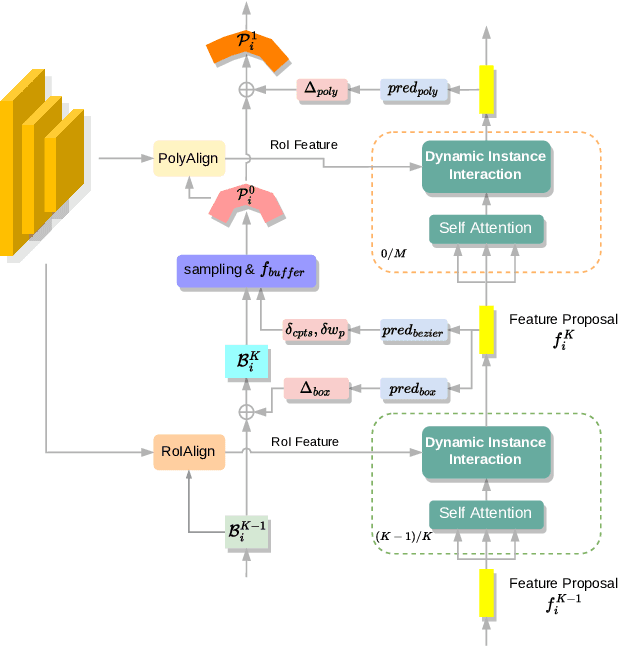

Abstract:Recently, Transformer-based text detection techniques have sought to predict polygons by encoding the coordinates of individual boundary vertices using distinct query features. However, this approach incurs a significant memory overhead and struggles to effectively capture the intricate relationships between vertices belonging to the same instance. Consequently, irregular text layouts often lead to the prediction of outlined vertices, diminishing the quality of results. To address these challenges, we present an innovative approach rooted in Sparse R-CNN: a cascade decoding pipeline for polygon prediction. Our method ensures precision by iteratively refining polygon predictions, considering both the scale and location of preceding results. Leveraging this stabilized regression pipeline, even employing just a single feature vector to guide polygon instance regression yields promising detection results. Simultaneously, the leverage of instance-level feature proposal substantially enhances memory efficiency (>50% less vs. the state-of-the-art method DPText-DETR) and reduces inference speed (>40% less vs. DPText-DETR) with minor performance drop on benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge