Variational Learning of Gaussian Process Latent Variable Models through Stochastic Gradient Annealed Importance Sampling

Gaussian Process Latent Variable Models (GPLVMs) have become increasingly popular for unsupervised tasks such as dimensionality reduction and missing data recovery due to their flexibility and non-linear nature. An importance-weighted version of the Bayesian GPLVMs has been proposed to obtain a tighter variational bound. However, this version of the approach is primarily limited to analyzing simple data structures, as the generation of an effective proposal distribution can become quite challenging in high-dimensional spaces or with complex data sets. In this work, we propose an Annealed Importance Sampling (AIS) approach to address these issues. By transforming the posterior into a sequence of intermediate distributions using annealing, we combine the strengths of Sequential Monte Carlo samplers and VI to explore a wider range of posterior distributions and gradually approach the target distribution. We further propose an efficient algorithm by reparameterizing all variables in the evidence lower bound (ELBO). Experimental results on both toy and image datasets demonstrate that our method outperforms state-of-the-art methods in terms of tighter variational bounds, higher log-likelihoods, and more robust convergence.

Entropy-Informed Weighting Channel Normalizing Flow

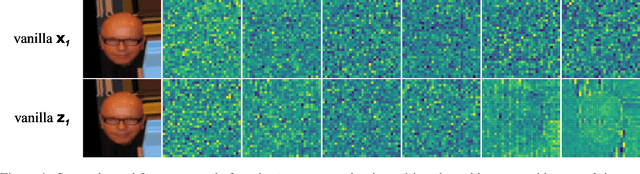
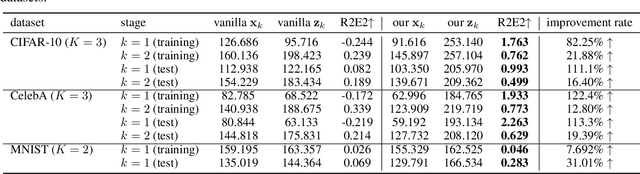
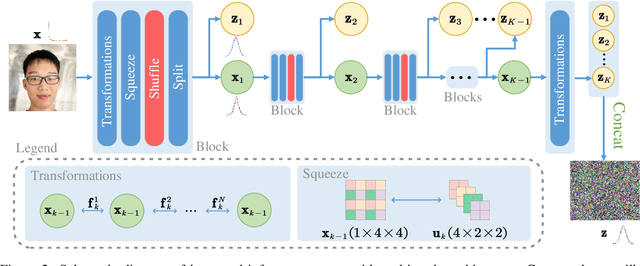
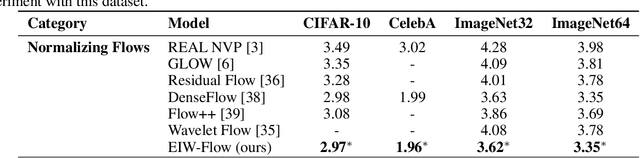
Normalizing Flows (NFs) have gained popularity among deep generative models due to their ability to provide exact likelihood estimation and efficient sampling. However, a crucial limitation of NFs is their substantial memory requirements, arising from maintaining the dimension of the latent space equal to that of the input space. Multi-scale architectures bypass this limitation by progressively reducing the dimension of latent variables while ensuring reversibility. Existing multi-scale architectures split the latent variables in a simple, static manner at the channel level, compromising NFs' expressive power. To address this issue, we propose a regularized and feature-dependent $\mathtt{Shuffle}$ operation and integrate it into vanilla multi-scale architecture. This operation heuristically generates channel-wise weights and adaptively shuffles latent variables before splitting them with these weights. We observe that such operation guides the variables to evolve in the direction of entropy increase, hence we refer to NFs with the $\mathtt{Shuffle}$ operation as \emph{Entropy-Informed Weighting Channel Normalizing Flow} (EIW-Flow). Experimental results indicate that the EIW-Flow achieves state-of-the-art density estimation results and comparable sample quality on CIFAR-10, CelebA and ImageNet datasets, with negligible additional computational overhead.

Efficient Personalized Text-to-image Generation by Leveraging Textual Subspace

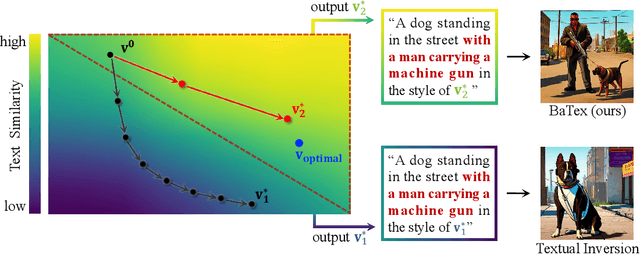
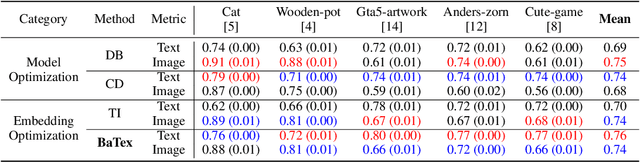
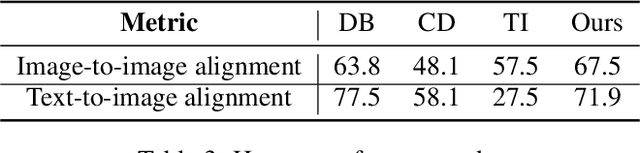
Personalized text-to-image generation has attracted unprecedented attention in the recent few years due to its unique capability of generating highly-personalized images via using the input concept dataset and novel textual prompt. However, previous methods solely focus on the performance of the reconstruction task, degrading its ability to combine with different textual prompt. Besides, optimizing in the high-dimensional embedding space usually leads to unnecessary time-consuming training process and slow convergence. To address these issues, we propose an efficient method to explore the target embedding in a textual subspace, drawing inspiration from the self-expressiveness property. Additionally, we propose an efficient selection strategy for determining the basis vectors of the textual subspace. The experimental evaluations demonstrate that the learned embedding can not only faithfully reconstruct input image, but also significantly improves its alignment with novel input textual prompt. Furthermore, we observe that optimizing in the textual subspace leads to an significant improvement of the robustness to the initial word, relaxing the constraint that requires users to input the most relevant initial word. Our method opens the door to more efficient representation learning for personalized text-to-image generation.

ParCo: Part-Coordinating Text-to-Motion Synthesis

We study a challenging task: text-to-motion synthesis, aiming to generate motions that align with textual descriptions and exhibit coordinated movements. Currently, the part-based methods introduce part partition into the motion synthesis process to achieve finer-grained generation. However, these methods encounter challenges such as the lack of coordination between different part motions and difficulties for networks to understand part concepts. Moreover, introducing finer-grained part concepts poses computational complexity challenges. In this paper, we propose Part-Coordinating Text-to-Motion Synthesis (ParCo), endowed with enhanced capabilities for understanding part motions and communication among different part motion generators, ensuring a coordinated and fined-grained motion synthesis. Specifically, we discretize whole-body motion into multiple part motions to establish the prior concept of different parts. Afterward, we employ multiple lightweight generators designed to synthesize different part motions and coordinate them through our part coordination module. Our approach demonstrates superior performance on common benchmarks with economic computations, including HumanML3D and KIT-ML, providing substantial evidence of its effectiveness. Code is available at https://github.com/qrzou/ParCo .

Solution for Point Tracking Task of ICCV 1st Perception Test Challenge 2023

This report proposes an improved method for the Tracking Any Point (TAP) task, which tracks any physical surface through a video. Several existing approaches have explored the TAP by considering the temporal relationships to obtain smooth point motion trajectories, however, they still suffer from the cumulative error caused by temporal prediction. To address this issue, we propose a simple yet effective approach called TAP with confident static points (TAPIR+), which focuses on rectifying the tracking of the static point in the videos shot by a static camera. To clarify, our approach contains two key components: (1) Multi-granularity Camera Motion Detection, which could identify the video sequence by the static camera shot. (2) CMR-based point trajectory prediction with one moving object segmentation approach to isolate the static point from the moving object. Our approach ranked first in the final test with a score of 0.46.

Neural Operator Variational Inference based on Regularized Stein Discrepancy for Deep Gaussian Processes

Deep Gaussian Process (DGP) models offer a powerful nonparametric approach for Bayesian inference, but exact inference is typically intractable, motivating the use of various approximations. However, existing approaches, such as mean-field Gaussian assumptions, limit the expressiveness and efficacy of DGP models, while stochastic approximation can be computationally expensive. To tackle these challenges, we introduce Neural Operator Variational Inference (NOVI) for Deep Gaussian Processes. NOVI uses a neural generator to obtain a sampler and minimizes the Regularized Stein Discrepancy in L2 space between the generated distribution and true posterior. We solve the minimax problem using Monte Carlo estimation and subsampling stochastic optimization techniques. We demonstrate that the bias introduced by our method can be controlled by multiplying the Fisher divergence with a constant, which leads to robust error control and ensures the stability and precision of the algorithm. Our experiments on datasets ranging from hundreds to tens of thousands demonstrate the effectiveness and the faster convergence rate of the proposed method. We achieve a classification accuracy of 93.56 on the CIFAR10 dataset, outperforming SOTA Gaussian process methods. Furthermore, our method guarantees theoretically controlled prediction error for DGP models and demonstrates remarkable performance on various datasets. We are optimistic that NOVI has the potential to enhance the performance of deep Bayesian nonparametric models and could have significant implications for various practical applications

Double Normalizing Flows: Flexible Bayesian Gaussian Process ODEs Learning

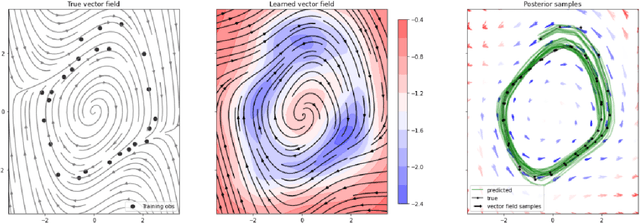
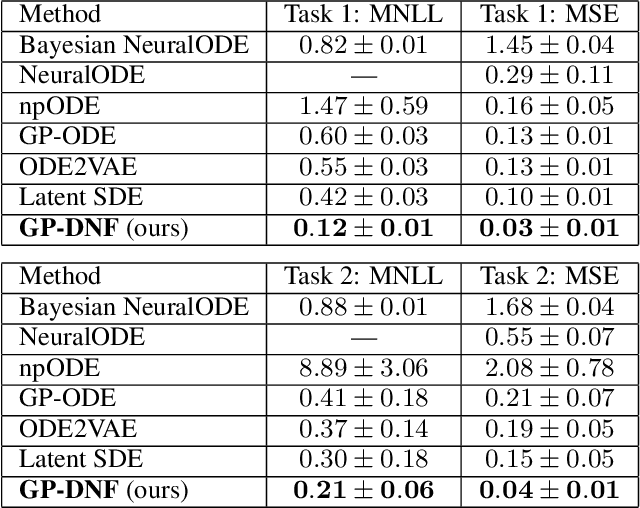
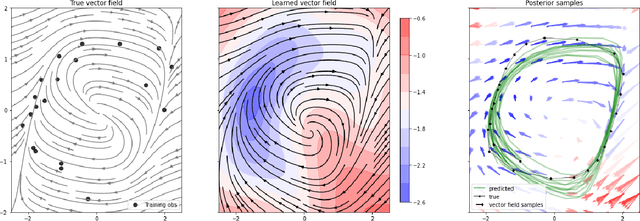
Recently, Gaussian processes have been utilized to model the vector field of continuous dynamical systems. Bayesian inference for such models \cite{hegde2022variational} has been extensively studied and has been applied in tasks such as time series prediction, providing uncertain estimates. However, previous Gaussian Process Ordinary Differential Equation (ODE) models may underperform on datasets with non-Gaussian process priors, as their constrained priors and mean-field posteriors may lack flexibility. To address this limitation, we incorporate normalizing flows to reparameterize the vector field of ODEs, resulting in a more flexible and expressive prior distribution. Additionally, due to the analytically tractable probability density functions of normalizing flows, we apply them to the posterior inference of GP ODEs, generating a non-Gaussian posterior. Through these dual applications of normalizing flows, our model improves accuracy and uncertainty estimates for Bayesian Gaussian Process ODEs. The effectiveness of our approach is demonstrated on simulated dynamical systems and real-world human motion data, including tasks such as time series prediction and missing data recovery. Experimental results indicate that our proposed method effectively captures model uncertainty while improving accuracy.

TO-FLOW: Efficient Continuous Normalizing Flows with Temporal Optimization adjoint with Moving Speed

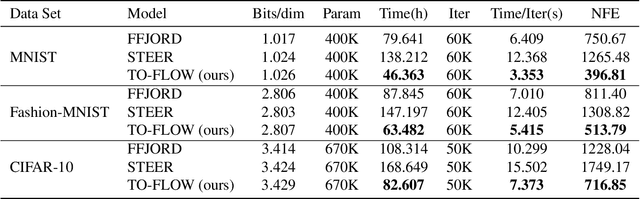
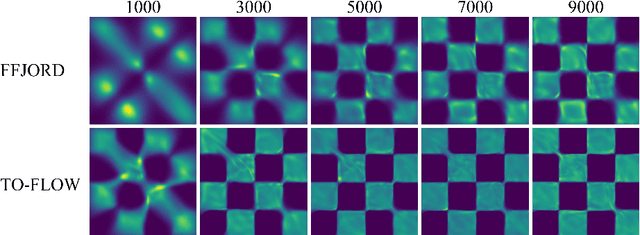
Continuous normalizing flows (CNFs) construct invertible mappings between an arbitrary complex distribution and an isotropic Gaussian distribution using Neural Ordinary Differential Equations (neural ODEs). It has not been tractable on large datasets due to the incremental complexity of the neural ODE training. Optimal Transport theory has been applied to regularize the dynamics of the ODE to speed up training in recent works. In this paper, a temporal optimization is proposed by optimizing the evolutionary time for forward propagation of the neural ODE training. In this appoach, we optimize the network weights of the CNF alternately with evolutionary time by coordinate descent. Further with temporal regularization, stability of the evolution is ensured. This approach can be used in conjunction with the original regularization approach. We have experimentally demonstrated that the proposed approach can significantly accelerate training without sacrifying performance over baseline models.