Dequantified Diffusion Schrödinger Bridge for Density Ratio Estimation

Density ratio estimation is fundamental to tasks involving $f$-divergences, yet existing methods often fail under significantly different distributions or inadequately overlap supports, suffering from the \textit{density-chasm} and the \textit{support-chasm} problems. Additionally, prior approaches yield divergent time scores near boundaries, leading to instability. We propose $\text{D}^3\text{RE}$, a unified framework for robust and efficient density ratio estimation. It introduces the Dequantified Diffusion-Bridge Interpolant (DDBI), which expands support coverage and stabilizes time scores via diffusion bridges and Gaussian dequantization. Building on DDBI, the Dequantified Schr\"odinger-Bridge Interpolant (DSBI) incorporates optimal transport to solve the Schr\"odinger bridge problem, enhancing accuracy and efficiency. Our method offers uniform approximation and bounded time scores in theory, and outperforms baselines empirically in mutual information and density estimation tasks.

Flexible Bayesian Last Layer Models Using Implicit Priors and Diffusion Posterior Sampling

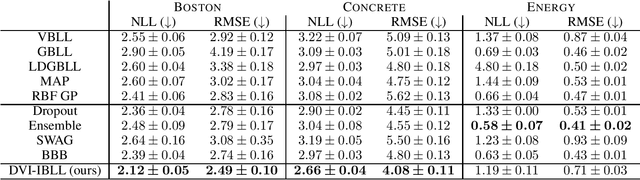
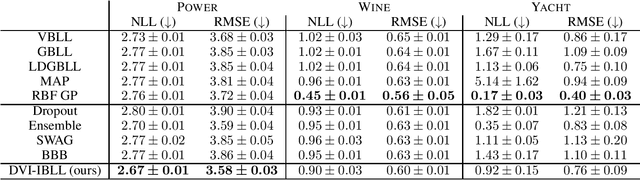
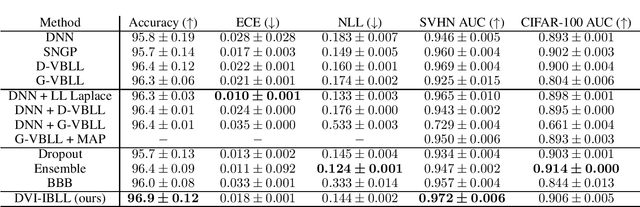
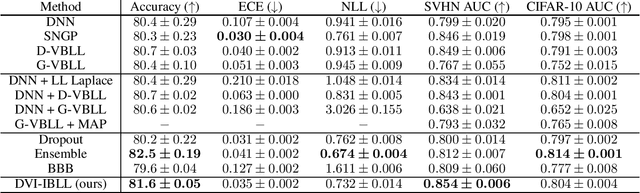
Bayesian Last Layer (BLL) models focus solely on uncertainty in the output layer of neural networks, demonstrating comparable performance to more complex Bayesian models. However, the use of Gaussian priors for last layer weights in Bayesian Last Layer (BLL) models limits their expressive capacity when faced with non-Gaussian, outlier-rich, or high-dimensional datasets. To address this shortfall, we introduce a novel approach that combines diffusion techniques and implicit priors for variational learning of Bayesian last layer weights. This method leverages implicit distributions for modeling weight priors in BLL, coupled with diffusion samplers for approximating true posterior predictions, thereby establishing a comprehensive Bayesian prior and posterior estimation strategy. By delivering an explicit and computationally efficient variational lower bound, our method aims to augment the expressive abilities of BLL models, enhancing model accuracy, calibration, and out-of-distribution detection proficiency. Through detailed exploration and experimental validation, We showcase the method's potential for improving predictive accuracy and uncertainty quantification while ensuring computational efficiency.

Entropy-Informed Weighting Channel Normalizing Flow

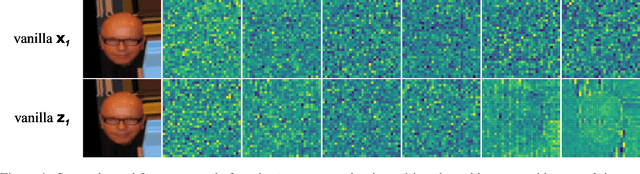
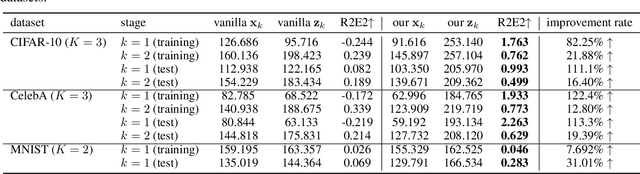
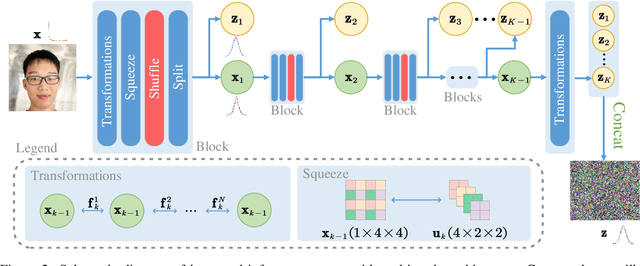
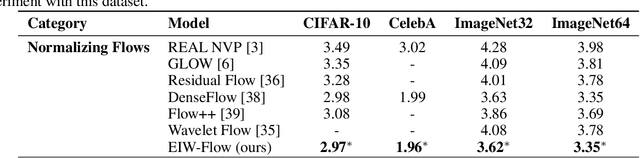
Normalizing Flows (NFs) have gained popularity among deep generative models due to their ability to provide exact likelihood estimation and efficient sampling. However, a crucial limitation of NFs is their substantial memory requirements, arising from maintaining the dimension of the latent space equal to that of the input space. Multi-scale architectures bypass this limitation by progressively reducing the dimension of latent variables while ensuring reversibility. Existing multi-scale architectures split the latent variables in a simple, static manner at the channel level, compromising NFs' expressive power. To address this issue, we propose a regularized and feature-dependent $\mathtt{Shuffle}$ operation and integrate it into vanilla multi-scale architecture. This operation heuristically generates channel-wise weights and adaptively shuffles latent variables before splitting them with these weights. We observe that such operation guides the variables to evolve in the direction of entropy increase, hence we refer to NFs with the $\mathtt{Shuffle}$ operation as \emph{Entropy-Informed Weighting Channel Normalizing Flow} (EIW-Flow). Experimental results indicate that the EIW-Flow achieves state-of-the-art density estimation results and comparable sample quality on CIFAR-10, CelebA and ImageNet datasets, with negligible additional computational overhead.

SciRE-Solver: Efficient Sampling of Diffusion Probabilistic Models by Score-integrand Solver with Recursive Derivative Estimation

Diffusion probabilistic models (DPMs) are a powerful class of generative models known for their ability to generate high-fidelity image samples. A major challenge in the implementation of DPMs is the slow sampling process. In this work, we bring a high-efficiency sampler for DPMs. Specifically, we propose a score-based exact solution paradigm for the diffusion ODEs corresponding to the sampling process of DPMs, which introduces a new perspective on developing numerical algorithms for solving diffusion ODEs. To achieve an efficient sampler, we propose a recursive derivative estimation (RDE) method to reduce the estimation error. With our proposed solution paradigm and RDE method, we propose the score-integrand solver with the convergence order guarantee as efficient solver (SciRE-Solver) for solving diffusion ODEs. The SciRE-Solver attains state-of-the-art (SOTA) sampling performance with a limited number of score function evaluations (NFE) on both discrete-time and continuous-time DPMs in comparison to existing training-free sampling algorithms. Such as, we achieve $3.48$ FID with $12$ NFE and $2.42$ FID with $20$ NFE for continuous-time DPMs on CIFAR10, respectively. Different from other samplers, SciRE-Solver has the promising potential to surpass the FIDs achieved in the original papers of some pre-trained models with a small NFEs. For example, we reach SOTA value of $2.40$ FID with $100$ NFE for continuous-time DPM and of $3.15$ FID with $84$ NFE for discrete-time DPM on CIFAR-10, as well as of $2.17$ ($2.02$) FID with $18$ ($50$) NFE for discrete-time DPM on CelebA 64$\times$64.