Variational Learning of Gaussian Process Latent Variable Models through Stochastic Gradient Annealed Importance Sampling

Gaussian Process Latent Variable Models (GPLVMs) have become increasingly popular for unsupervised tasks such as dimensionality reduction and missing data recovery due to their flexibility and non-linear nature. An importance-weighted version of the Bayesian GPLVMs has been proposed to obtain a tighter variational bound. However, this version of the approach is primarily limited to analyzing simple data structures, as the generation of an effective proposal distribution can become quite challenging in high-dimensional spaces or with complex data sets. In this work, we propose an Annealed Importance Sampling (AIS) approach to address these issues. By transforming the posterior into a sequence of intermediate distributions using annealing, we combine the strengths of Sequential Monte Carlo samplers and VI to explore a wider range of posterior distributions and gradually approach the target distribution. We further propose an efficient algorithm by reparameterizing all variables in the evidence lower bound (ELBO). Experimental results on both toy and image datasets demonstrate that our method outperforms state-of-the-art methods in terms of tighter variational bounds, higher log-likelihoods, and more robust convergence.

Fully Bayesian Differential Gaussian Processes through Stochastic Differential Equations

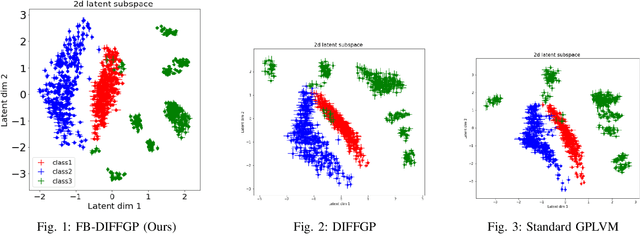
Traditional deep Gaussian processes model the data evolution using a discrete hierarchy, whereas differential Gaussian processes (DIFFGPs) represent the evolution as an infinitely deep Gaussian process. However, prior DIFFGP methods often overlook the uncertainty of kernel hyperparameters and assume them to be fixed and time-invariant, failing to leverage the unique synergy between continuous-time models and approximate inference. In this work, we propose a fully Bayesian approach that treats the kernel hyperparameters as random variables and constructs coupled stochastic differential equations (SDEs) to learn their posterior distribution and that of inducing points. By incorporating estimation uncertainty on hyperparameters, our method enhances the model's flexibility and adaptability to complex dynamics. Additionally, our approach provides a time-varying, comprehensive, and realistic posterior approximation through coupling variables using SDE methods. Experimental results demonstrate the advantages of our method over traditional approaches, showcasing its superior performance in terms of flexibility, accuracy, and other metrics. Our work opens up exciting research avenues for advancing Bayesian inference and offers a powerful modeling tool for continuous-time Gaussian processes.

Flexible Bayesian Last Layer Models Using Implicit Priors and Diffusion Posterior Sampling

Bayesian Last Layer (BLL) models focus solely on uncertainty in the output layer of neural networks, demonstrating comparable performance to more complex Bayesian models. However, the use of Gaussian priors for last layer weights in Bayesian Last Layer (BLL) models limits their expressive capacity when faced with non-Gaussian, outlier-rich, or high-dimensional datasets. To address this shortfall, we introduce a novel approach that combines diffusion techniques and implicit priors for variational learning of Bayesian last layer weights. This method leverages implicit distributions for modeling weight priors in BLL, coupled with diffusion samplers for approximating true posterior predictions, thereby establishing a comprehensive Bayesian prior and posterior estimation strategy. By delivering an explicit and computationally efficient variational lower bound, our method aims to augment the expressive abilities of BLL models, enhancing model accuracy, calibration, and out-of-distribution detection proficiency. Through detailed exploration and experimental validation, We showcase the method's potential for improving predictive accuracy and uncertainty quantification while ensuring computational efficiency.

Neural Operator Variational Inference based on Regularized Stein Discrepancy for Deep Gaussian Processes

Deep Gaussian Process (DGP) models offer a powerful nonparametric approach for Bayesian inference, but exact inference is typically intractable, motivating the use of various approximations. However, existing approaches, such as mean-field Gaussian assumptions, limit the expressiveness and efficacy of DGP models, while stochastic approximation can be computationally expensive. To tackle these challenges, we introduce Neural Operator Variational Inference (NOVI) for Deep Gaussian Processes. NOVI uses a neural generator to obtain a sampler and minimizes the Regularized Stein Discrepancy in L2 space between the generated distribution and true posterior. We solve the minimax problem using Monte Carlo estimation and subsampling stochastic optimization techniques. We demonstrate that the bias introduced by our method can be controlled by multiplying the Fisher divergence with a constant, which leads to robust error control and ensures the stability and precision of the algorithm. Our experiments on datasets ranging from hundreds to tens of thousands demonstrate the effectiveness and the faster convergence rate of the proposed method. We achieve a classification accuracy of 93.56 on the CIFAR10 dataset, outperforming SOTA Gaussian process methods. Furthermore, our method guarantees theoretically controlled prediction error for DGP models and demonstrates remarkable performance on various datasets. We are optimistic that NOVI has the potential to enhance the performance of deep Bayesian nonparametric models and could have significant implications for various practical applications

Double Normalizing Flows: Flexible Bayesian Gaussian Process ODEs Learning

Recently, Gaussian processes have been utilized to model the vector field of continuous dynamical systems. Bayesian inference for such models \cite{hegde2022variational} has been extensively studied and has been applied in tasks such as time series prediction, providing uncertain estimates. However, previous Gaussian Process Ordinary Differential Equation (ODE) models may underperform on datasets with non-Gaussian process priors, as their constrained priors and mean-field posteriors may lack flexibility. To address this limitation, we incorporate normalizing flows to reparameterize the vector field of ODEs, resulting in a more flexible and expressive prior distribution. Additionally, due to the analytically tractable probability density functions of normalizing flows, we apply them to the posterior inference of GP ODEs, generating a non-Gaussian posterior. Through these dual applications of normalizing flows, our model improves accuracy and uncertainty estimates for Bayesian Gaussian Process ODEs. The effectiveness of our approach is demonstrated on simulated dynamical systems and real-world human motion data, including tasks such as time series prediction and missing data recovery. Experimental results indicate that our proposed method effectively captures model uncertainty while improving accuracy.