Delu Zeng
Any-Step Density Ratio Estimation via Interval-Annealed Secant Alignment
Sep 05, 2025Abstract:Estimating density ratios is a fundamental problem in machine learning, but existing methods often trade off accuracy for efficiency. We propose \textit{Interval-annealed Secant Alignment Density Ratio Estimation (ISA-DRE)}, a framework that enables accurate, any-step estimation without numerical integration. Instead of modeling infinitesimal tangents as in prior methods, ISA-DRE learns a global secant function, defined as the expectation of all tangents over an interval, with provably lower variance, making it more suitable for neural approximation. This is made possible by the \emph{Secant Alignment Identity}, a self-consistency condition that formally connects the secant with its underlying tangent representations. To mitigate instability during early training, we introduce \emph{Contraction Interval Annealing}, a curriculum strategy that gradually expands the alignment interval during training. This process induces a contraction mapping, which improves convergence and training stability. Empirically, ISA-DRE achieves competitive accuracy with significantly fewer function evaluations compared to prior methods, resulting in much faster inference and making it well suited for real-time and interactive applications.
Neural Bridge Processes
Aug 10, 2025Abstract:Learning stochastic functions from partially observed context-target pairs is a fundamental problem in probabilistic modeling. Traditional models like Gaussian Processes (GPs) face scalability issues with large datasets and assume Gaussianity, limiting their applicability. While Neural Processes (NPs) offer more flexibility, they struggle with capturing complex, multi-modal target distributions. Neural Diffusion Processes (NDPs) enhance expressivity through a learned diffusion process but rely solely on conditional signals in the denoising network, resulting in weak input coupling from an unconditional forward process and semantic mismatch at the diffusion endpoint. In this work, we propose Neural Bridge Processes (NBPs), a novel method for modeling stochastic functions where inputs x act as dynamic anchors for the entire diffusion trajectory. By reformulating the forward kernel to explicitly depend on x, NBP enforces a constrained path that strictly terminates at the supervised target. This approach not only provides stronger gradient signals but also guarantees endpoint coherence. We validate NBPs on synthetic data, EEG signal regression and image regression tasks, achieving substantial improvements over baselines. These results underscore the effectiveness of DDPM-style bridge sampling in enhancing both performance and theoretical consistency for structured prediction tasks.
Dequantified Diffusion Schrödinger Bridge for Density Ratio Estimation
May 08, 2025Abstract:Density ratio estimation is fundamental to tasks involving $f$-divergences, yet existing methods often fail under significantly different distributions or inadequately overlap supports, suffering from the \textit{density-chasm} and the \textit{support-chasm} problems. Additionally, prior approaches yield divergent time scores near boundaries, leading to instability. We propose $\text{D}^3\text{RE}$, a unified framework for robust and efficient density ratio estimation. It introduces the Dequantified Diffusion-Bridge Interpolant (DDBI), which expands support coverage and stabilizes time scores via diffusion bridges and Gaussian dequantization. Building on DDBI, the Dequantified Schr\"odinger-Bridge Interpolant (DSBI) incorporates optimal transport to solve the Schr\"odinger bridge problem, enhancing accuracy and efficiency. Our method offers uniform approximation and bounded time scores in theory, and outperforms baselines empirically in mutual information and density estimation tasks.
Information Geometry and Beta Link for Optimizing Sparse Variational Student-t Processes
Aug 13, 2024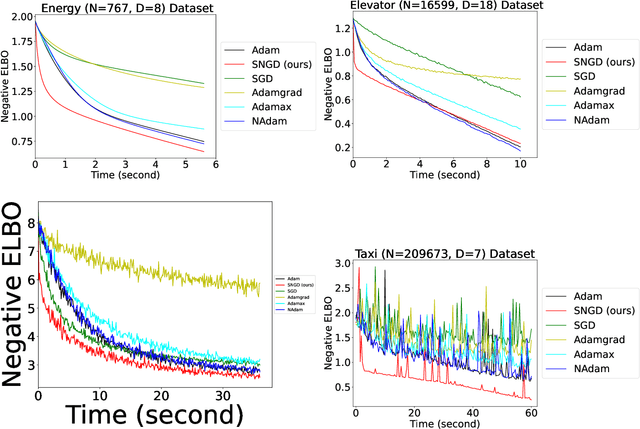
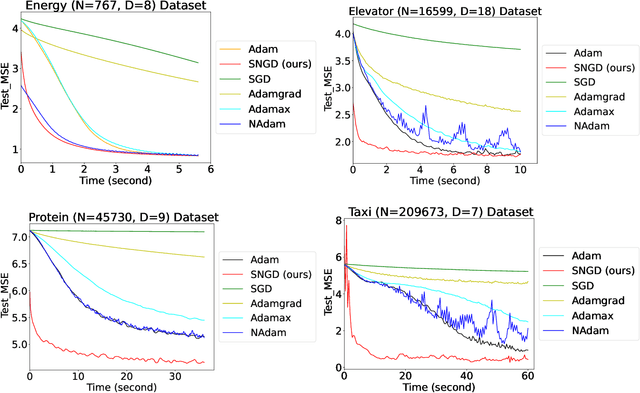
Abstract:Recently, a sparse version of Student-t Processes, termed sparse variational Student-t Processes, has been proposed to enhance computational efficiency and flexibility for real-world datasets using stochastic gradient descent. However, traditional gradient descent methods like Adam may not fully exploit the parameter space geometry, potentially leading to slower convergence and suboptimal performance. To mitigate these issues, we adopt natural gradient methods from information geometry for variational parameter optimization of Student-t Processes. This approach leverages the curvature and structure of the parameter space, utilizing tools such as the Fisher information matrix which is linked to the Beta function in our model. This method provides robust mathematical support for the natural gradient algorithm when using Student's t-distribution as the variational distribution. Additionally, we present a mini-batch algorithm for efficiently computing natural gradients. Experimental results across four benchmark datasets demonstrate that our method consistently accelerates convergence speed.
Variational Learning of Gaussian Process Latent Variable Models through Stochastic Gradient Annealed Importance Sampling
Aug 13, 2024



Abstract:Gaussian Process Latent Variable Models (GPLVMs) have become increasingly popular for unsupervised tasks such as dimensionality reduction and missing data recovery due to their flexibility and non-linear nature. An importance-weighted version of the Bayesian GPLVMs has been proposed to obtain a tighter variational bound. However, this version of the approach is primarily limited to analyzing simple data structures, as the generation of an effective proposal distribution can become quite challenging in high-dimensional spaces or with complex data sets. In this work, we propose an Annealed Importance Sampling (AIS) approach to address these issues. By transforming the posterior into a sequence of intermediate distributions using annealing, we combine the strengths of Sequential Monte Carlo samplers and VI to explore a wider range of posterior distributions and gradually approach the target distribution. We further propose an efficient algorithm by reparameterizing all variables in the evidence lower bound (ELBO). Experimental results on both toy and image datasets demonstrate that our method outperforms state-of-the-art methods in terms of tighter variational bounds, higher log-likelihoods, and more robust convergence.
Fully Bayesian Differential Gaussian Processes through Stochastic Differential Equations
Aug 12, 2024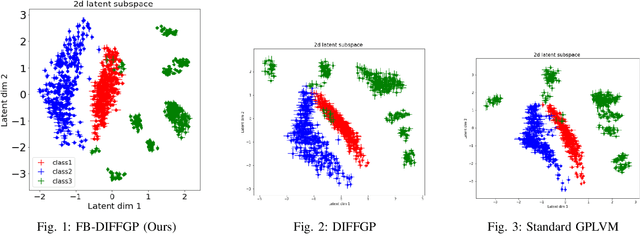

Abstract:Traditional deep Gaussian processes model the data evolution using a discrete hierarchy, whereas differential Gaussian processes (DIFFGPs) represent the evolution as an infinitely deep Gaussian process. However, prior DIFFGP methods often overlook the uncertainty of kernel hyperparameters and assume them to be fixed and time-invariant, failing to leverage the unique synergy between continuous-time models and approximate inference. In this work, we propose a fully Bayesian approach that treats the kernel hyperparameters as random variables and constructs coupled stochastic differential equations (SDEs) to learn their posterior distribution and that of inducing points. By incorporating estimation uncertainty on hyperparameters, our method enhances the model's flexibility and adaptability to complex dynamics. Additionally, our approach provides a time-varying, comprehensive, and realistic posterior approximation through coupling variables using SDE methods. Experimental results demonstrate the advantages of our method over traditional approaches, showcasing its superior performance in terms of flexibility, accuracy, and other metrics. Our work opens up exciting research avenues for advancing Bayesian inference and offers a powerful modeling tool for continuous-time Gaussian processes.
Flexible Bayesian Last Layer Models Using Implicit Priors and Diffusion Posterior Sampling
Aug 07, 2024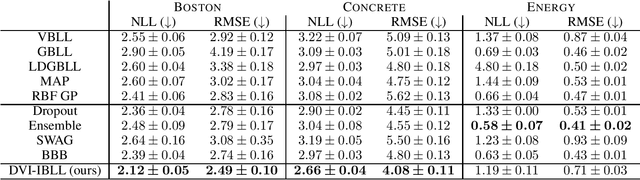
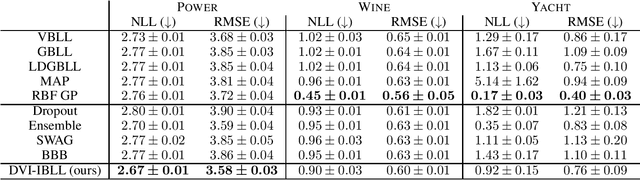
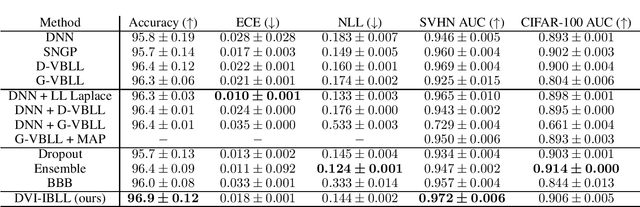
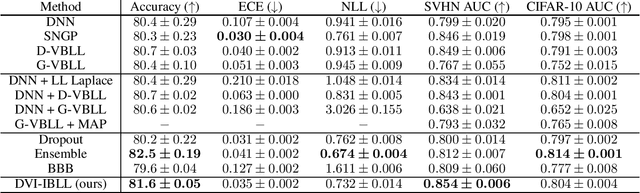
Abstract:Bayesian Last Layer (BLL) models focus solely on uncertainty in the output layer of neural networks, demonstrating comparable performance to more complex Bayesian models. However, the use of Gaussian priors for last layer weights in Bayesian Last Layer (BLL) models limits their expressive capacity when faced with non-Gaussian, outlier-rich, or high-dimensional datasets. To address this shortfall, we introduce a novel approach that combines diffusion techniques and implicit priors for variational learning of Bayesian last layer weights. This method leverages implicit distributions for modeling weight priors in BLL, coupled with diffusion samplers for approximating true posterior predictions, thereby establishing a comprehensive Bayesian prior and posterior estimation strategy. By delivering an explicit and computationally efficient variational lower bound, our method aims to augment the expressive abilities of BLL models, enhancing model accuracy, calibration, and out-of-distribution detection proficiency. Through detailed exploration and experimental validation, We showcase the method's potential for improving predictive accuracy and uncertainty quantification while ensuring computational efficiency.
Sparse Inducing Points in Deep Gaussian Processes: Enhancing Modeling with Denoising Diffusion Variational Inference
Jul 24, 2024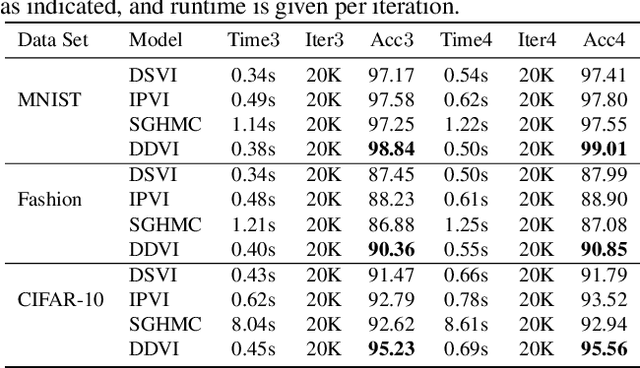
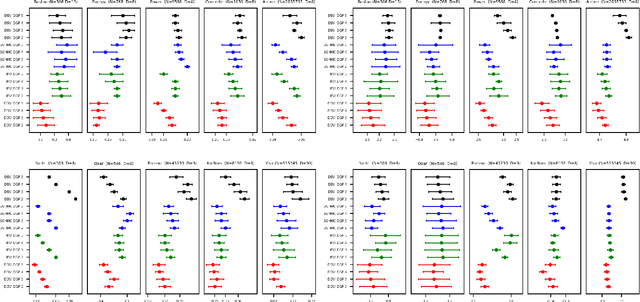
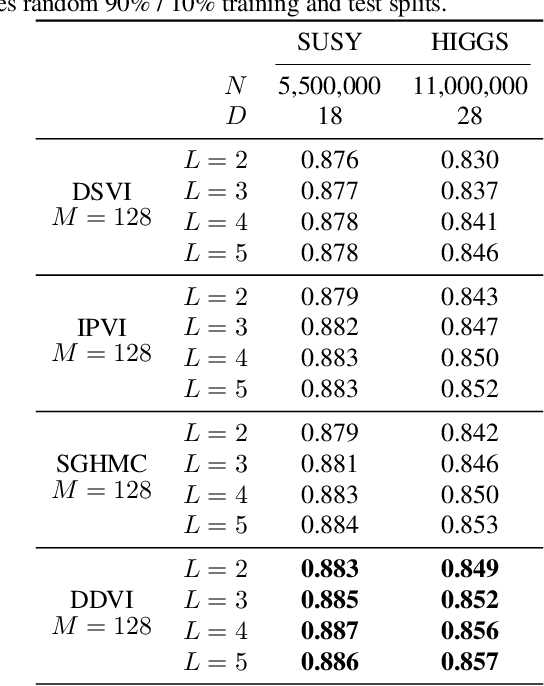

Abstract:Deep Gaussian processes (DGPs) provide a robust paradigm for Bayesian deep learning. In DGPs, a set of sparse integration locations called inducing points are selected to approximate the posterior distribution of the model. This is done to reduce computational complexity and improve model efficiency. However, inferring the posterior distribution of inducing points is not straightforward. Traditional variational inference approaches to posterior approximation often lead to significant bias. To address this issue, we propose an alternative method called Denoising Diffusion Variational Inference (DDVI) that uses a denoising diffusion stochastic differential equation (SDE) to generate posterior samples of inducing variables. We rely on score matching methods for denoising diffusion model to approximate score functions with a neural network. Furthermore, by combining classical mathematical theory of SDEs with the minimization of KL divergence between the approximate and true processes, we propose a novel explicit variational lower bound for the marginal likelihood function of DGP. Through experiments on various datasets and comparisons with baseline methods, we empirically demonstrate the effectiveness of DDVI for posterior inference of inducing points for DGP models.
Entropy-Informed Weighting Channel Normalizing Flow
Jul 06, 2024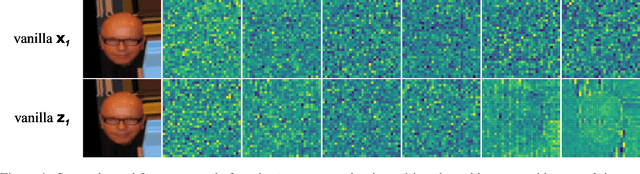
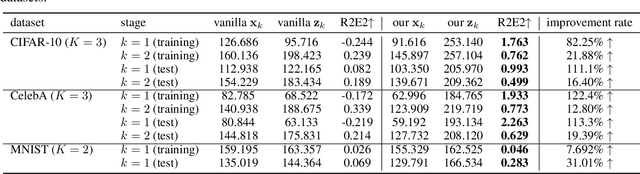
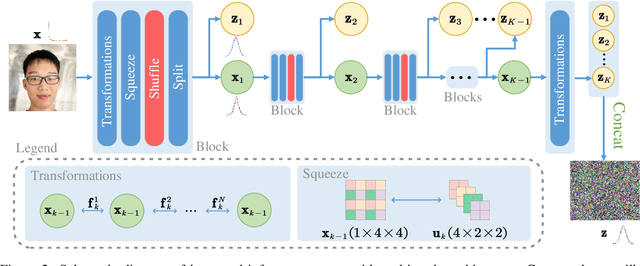
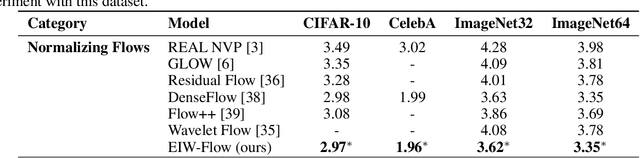
Abstract:Normalizing Flows (NFs) have gained popularity among deep generative models due to their ability to provide exact likelihood estimation and efficient sampling. However, a crucial limitation of NFs is their substantial memory requirements, arising from maintaining the dimension of the latent space equal to that of the input space. Multi-scale architectures bypass this limitation by progressively reducing the dimension of latent variables while ensuring reversibility. Existing multi-scale architectures split the latent variables in a simple, static manner at the channel level, compromising NFs' expressive power. To address this issue, we propose a regularized and feature-dependent $\mathtt{Shuffle}$ operation and integrate it into vanilla multi-scale architecture. This operation heuristically generates channel-wise weights and adaptively shuffles latent variables before splitting them with these weights. We observe that such operation guides the variables to evolve in the direction of entropy increase, hence we refer to NFs with the $\mathtt{Shuffle}$ operation as \emph{Entropy-Informed Weighting Channel Normalizing Flow} (EIW-Flow). Experimental results indicate that the EIW-Flow achieves state-of-the-art density estimation results and comparable sample quality on CIFAR-10, CelebA and ImageNet datasets, with negligible additional computational overhead.
Improve Cross-domain Mixed Sampling with Guidance Training for Adaptive Segmentation
Mar 22, 2024Abstract:Unsupervised Domain Adaptation (UDA) endeavors to adjust models trained on a source domain to perform well on a target domain without requiring additional annotations. In the context of domain adaptive semantic segmentation, which tackles UDA for dense prediction, the goal is to circumvent the need for costly pixel-level annotations. Typically, various prevailing methods baseline rely on constructing intermediate domains via cross-domain mixed sampling techniques to mitigate the performance decline caused by domain gaps. However, such approaches generate synthetic data that diverge from real-world distributions, potentially leading the model astray from the true target distribution. To address this challenge, we propose a novel auxiliary task called Guidance Training. This task facilitates the effective utilization of cross-domain mixed sampling techniques while mitigating distribution shifts from the real world. Specifically, Guidance Training guides the model to extract and reconstruct the target-domain feature distribution from mixed data, followed by decoding the reconstructed target-domain features to make pseudo-label predictions. Importantly, integrating Guidance Training incurs minimal training overhead and imposes no additional inference burden. We demonstrate the efficacy of our approach by integrating it with existing methods, consistently improving performance. The implementation will be available at https://github.com/Wenlve-Zhou/Guidance-Training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge