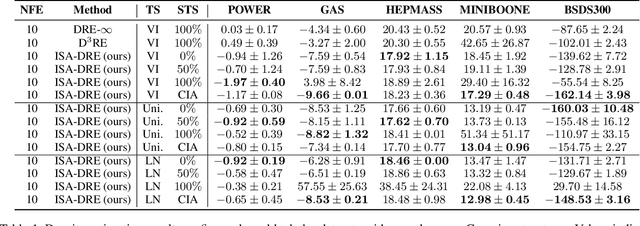
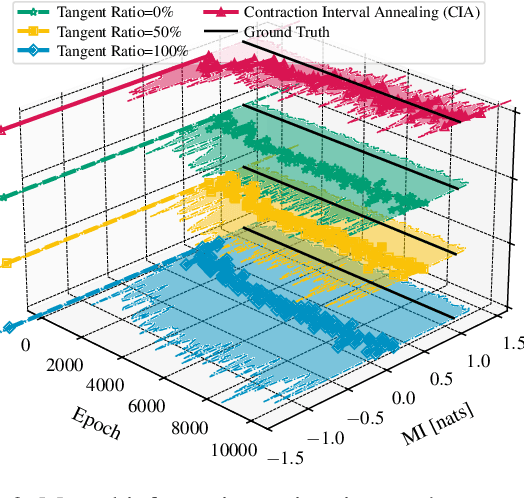
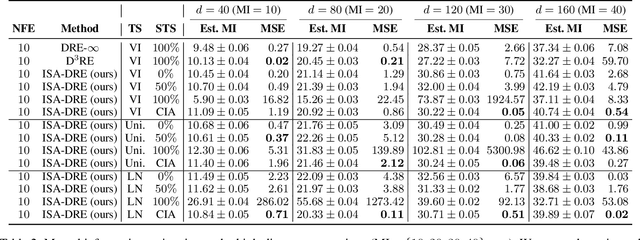
Any-Step Density Ratio Estimation via Interval-Annealed Secant Alignment

Estimating density ratios is a fundamental problem in machine learning, but existing methods often trade off accuracy for efficiency. We propose \textit{Interval-annealed Secant Alignment Density Ratio Estimation (ISA-DRE)}, a framework that enables accurate, any-step estimation without numerical integration. Instead of modeling infinitesimal tangents as in prior methods, ISA-DRE learns a global secant function, defined as the expectation of all tangents over an interval, with provably lower variance, making it more suitable for neural approximation. This is made possible by the \emph{Secant Alignment Identity}, a self-consistency condition that formally connects the secant with its underlying tangent representations. To mitigate instability during early training, we introduce \emph{Contraction Interval Annealing}, a curriculum strategy that gradually expands the alignment interval during training. This process induces a contraction mapping, which improves convergence and training stability. Empirically, ISA-DRE achieves competitive accuracy with significantly fewer function evaluations compared to prior methods, resulting in much faster inference and making it well suited for real-time and interactive applications.

Truncated Proximal Policy Optimization

Recently, test-time scaling Large Language Models (LLMs) have demonstrated exceptional reasoning capabilities across scientific and professional tasks by generating long chains-of-thought (CoT). As a crucial component for developing these reasoning models, reinforcement learning (RL), exemplified by Proximal Policy Optimization (PPO) and its variants, allows models to learn through trial and error. However, PPO can be time-consuming due to its inherent on-policy nature, which is further exacerbated by increasing response lengths. In this work, we propose Truncated Proximal Policy Optimization (T-PPO), a novel extension to PPO that improves training efficiency by streamlining policy update and length-restricted response generation. T-PPO mitigates the issue of low hardware utilization, an inherent drawback of fully synchronized long-generation procedures, where resources often sit idle during the waiting periods for complete rollouts. Our contributions are two-folds. First, we propose Extended Generalized Advantage Estimation (EGAE) for advantage estimation derived from incomplete responses while maintaining the integrity of policy learning. Second, we devise a computationally optimized mechanism that allows for the independent optimization of the policy and value models. By selectively filtering prompt and truncated tokens, this mechanism reduces redundant computations and accelerates the training process without sacrificing convergence performance. We demonstrate the effectiveness and efficacy of T-PPO on AIME 2024 with a 32B base model. The experimental results show that T-PPO improves the training efficiency of reasoning LLMs by up to 2.5x and outperforms its existing competitors.

VAPO: Efficient and Reliable Reinforcement Learning for Advanced Reasoning Tasks

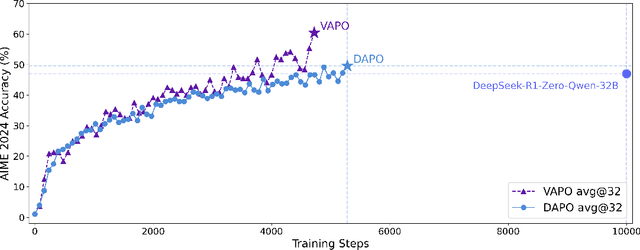
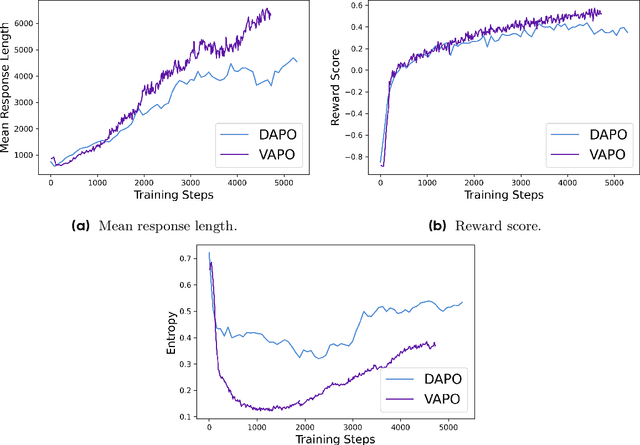
We present VAPO, Value-based Augmented Proximal Policy Optimization framework for reasoning models., a novel framework tailored for reasoning models within the value-based paradigm. Benchmarked the AIME 2024 dataset, VAPO, built on the Qwen 32B pre-trained model, attains a state-of-the-art score of $\mathbf{60.4}$. In direct comparison under identical experimental settings, VAPO outperforms the previously reported results of DeepSeek-R1-Zero-Qwen-32B and DAPO by more than 10 points. The training process of VAPO stands out for its stability and efficiency. It reaches state-of-the-art performance within a mere 5,000 steps. Moreover, across multiple independent runs, no training crashes occur, underscoring its reliability. This research delves into long chain-of-thought (long-CoT) reasoning using a value-based reinforcement learning framework. We pinpoint three key challenges that plague value-based methods: value model bias, the presence of heterogeneous sequence lengths, and the sparsity of reward signals. Through systematic design, VAPO offers an integrated solution that effectively alleviates these challenges, enabling enhanced performance in long-CoT reasoning tasks.

DAPO: An Open-Source LLM Reinforcement Learning System at Scale

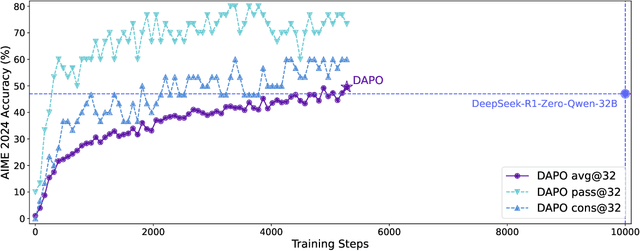
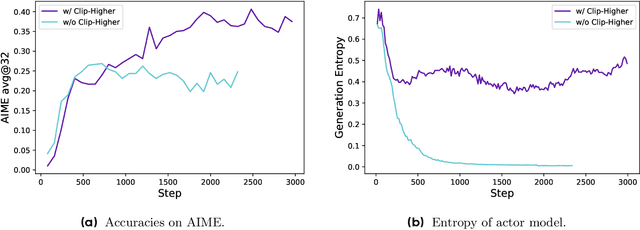
Inference scaling empowers LLMs with unprecedented reasoning ability, with reinforcement learning as the core technique to elicit complex reasoning. However, key technical details of state-of-the-art reasoning LLMs are concealed (such as in OpenAI o1 blog and DeepSeek R1 technical report), thus the community still struggles to reproduce their RL training results. We propose the $\textbf{D}$ecoupled Clip and $\textbf{D}$ynamic s$\textbf{A}$mpling $\textbf{P}$olicy $\textbf{O}$ptimization ($\textbf{DAPO}$) algorithm, and fully open-source a state-of-the-art large-scale RL system that achieves 50 points on AIME 2024 using Qwen2.5-32B base model. Unlike previous works that withhold training details, we introduce four key techniques of our algorithm that make large-scale LLM RL a success. In addition, we open-source our training code, which is built on the verl framework, along with a carefully curated and processed dataset. These components of our open-source system enhance reproducibility and support future research in large-scale LLM RL.

Natural Language Fine-Tuning

Large language model fine-tuning techniques typically depend on extensive labeled data, external guidance, and feedback, such as human alignment, scalar rewards, and demonstration. However, in practical application, the scarcity of specific knowledge poses unprecedented challenges to existing fine-tuning techniques. In this paper, focusing on fine-tuning tasks in specific domains with limited data, we introduce Natural Language Fine-Tuning (NLFT), which utilizes natural language for fine-tuning for the first time. By leveraging the strong language comprehension capability of the target LM, NLFT attaches the guidance of natural language to the token-level outputs. Then, saliency tokens are identified with calculated probabilities. Since linguistic information is effectively utilized in NLFT, our proposed method significantly reduces training costs. It markedly enhances training efficiency, comprehensively outperforming reinforcement fine-tuning algorithms in accuracy, time-saving, and resource conservation. Additionally, on the macro level, NLFT can be viewed as a token-level fine-grained optimization of SFT, thereby efficiently replacing the SFT process without the need for warm-up (as opposed to ReFT requiring multiple rounds of warm-up with SFT). Compared to SFT, NLFT does not increase the algorithmic complexity, maintaining O(n). Extensive experiments on the GSM8K dataset demonstrate that NLFT, with only 50 data instances, achieves an accuracy increase that exceeds SFT by 219%. Compared to ReFT, the time complexity and space complexity of NLFT are reduced by 78.27% and 92.24%, respectively. The superior technique of NLFT is paving the way for the deployment of various innovative LLM fine-tuning applications when resources are limited at network edges. Our code has been released at https://github.com/Julia-LiuJ/NLFT.

Fully Bayesian Differential Gaussian Processes through Stochastic Differential Equations

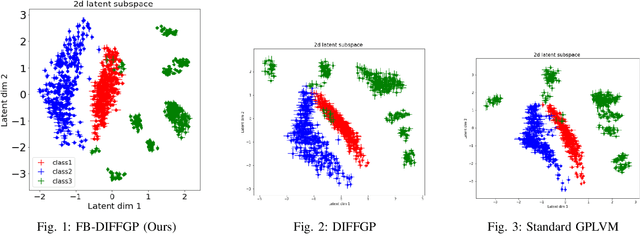
Traditional deep Gaussian processes model the data evolution using a discrete hierarchy, whereas differential Gaussian processes (DIFFGPs) represent the evolution as an infinitely deep Gaussian process. However, prior DIFFGP methods often overlook the uncertainty of kernel hyperparameters and assume them to be fixed and time-invariant, failing to leverage the unique synergy between continuous-time models and approximate inference. In this work, we propose a fully Bayesian approach that treats the kernel hyperparameters as random variables and constructs coupled stochastic differential equations (SDEs) to learn their posterior distribution and that of inducing points. By incorporating estimation uncertainty on hyperparameters, our method enhances the model's flexibility and adaptability to complex dynamics. Additionally, our approach provides a time-varying, comprehensive, and realistic posterior approximation through coupling variables using SDE methods. Experimental results demonstrate the advantages of our method over traditional approaches, showcasing its superior performance in terms of flexibility, accuracy, and other metrics. Our work opens up exciting research avenues for advancing Bayesian inference and offers a powerful modeling tool for continuous-time Gaussian processes.

Flexible Bayesian Last Layer Models Using Implicit Priors and Diffusion Posterior Sampling

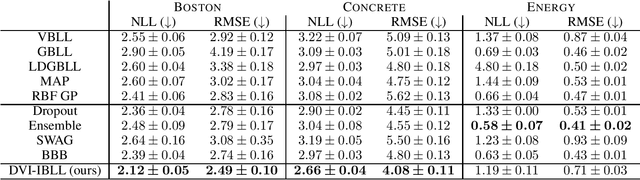
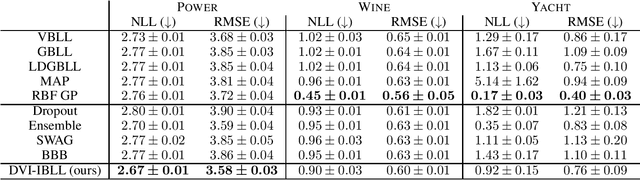
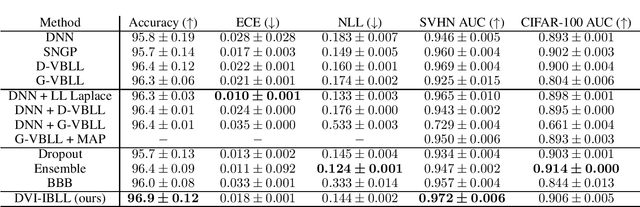
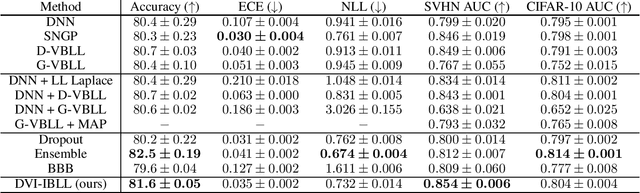
Bayesian Last Layer (BLL) models focus solely on uncertainty in the output layer of neural networks, demonstrating comparable performance to more complex Bayesian models. However, the use of Gaussian priors for last layer weights in Bayesian Last Layer (BLL) models limits their expressive capacity when faced with non-Gaussian, outlier-rich, or high-dimensional datasets. To address this shortfall, we introduce a novel approach that combines diffusion techniques and implicit priors for variational learning of Bayesian last layer weights. This method leverages implicit distributions for modeling weight priors in BLL, coupled with diffusion samplers for approximating true posterior predictions, thereby establishing a comprehensive Bayesian prior and posterior estimation strategy. By delivering an explicit and computationally efficient variational lower bound, our method aims to augment the expressive abilities of BLL models, enhancing model accuracy, calibration, and out-of-distribution detection proficiency. Through detailed exploration and experimental validation, We showcase the method's potential for improving predictive accuracy and uncertainty quantification while ensuring computational efficiency.

Tessel: Boosting Distributed Execution of Large DNN Models via Flexible Schedule Search

Increasingly complex and diverse deep neural network (DNN) models necessitate distributing the execution across multiple devices for training and inference tasks, and also require carefully planned schedules for performance. However, existing practices often rely on predefined schedules that may not fully exploit the benefits of emerging diverse model-aware operator placement strategies. Handcrafting high-efficiency schedules can be challenging due to the large and varying schedule space. This paper presents Tessel, an automated system that searches for efficient schedules for distributed DNN training and inference for diverse operator placement strategies. To reduce search costs, Tessel leverages the insight that the most efficient schedules often exhibit repetitive pattern (repetend) across different data inputs. This leads to a two-phase approach: repetend construction and schedule completion. By exploring schedules for various operator placement strategies, Tessel significantly improves both training and inference performance. Experiments with representative DNN models demonstrate that Tessel achieves up to 5.5x training performance speedup and up to 38% inference latency reduction.

SuperScaler: Supporting Flexible DNN Parallelization via a Unified Abstraction

With the growing model size, deep neural networks (DNN) are increasingly trained over massive GPU accelerators, which demands a proper parallelization plan that transforms a DNN model into fine-grained tasks and then schedules them to GPUs for execution. Due to the large search space, the contemporary parallelization plan generators often rely on empirical rules that couple transformation and scheduling, and fall short in exploring more flexible schedules that yield better memory usage and compute efficiency. This tension can be exacerbated by the emerging models with increasing complexity in their structure and model size. SuperScaler is a system that facilitates the design and generation of highly flexible parallelization plans. It formulates the plan design and generation into three sequential phases explicitly: model transformation, space-time scheduling, and data dependency preserving. Such a principled approach decouples multiple seemingly intertwined factors and enables the composition of highly flexible parallelization plans. As a result, SuperScaler can not only generate empirical parallelization plans, but also construct new plans that achieve up to 3.5X speedup compared to state-of-the-art solutions like DeepSpeed, Megatron and Alpa, for emerging DNN models like Swin-Transformer and AlphaFold2, as well as well-optimized models like GPT-3.