Fully Bayesian Differential Gaussian Processes through Stochastic Differential Equations
Paper and Code
Aug 12, 2024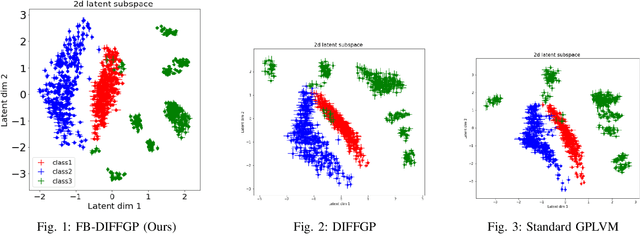

Traditional deep Gaussian processes model the data evolution using a discrete hierarchy, whereas differential Gaussian processes (DIFFGPs) represent the evolution as an infinitely deep Gaussian process. However, prior DIFFGP methods often overlook the uncertainty of kernel hyperparameters and assume them to be fixed and time-invariant, failing to leverage the unique synergy between continuous-time models and approximate inference. In this work, we propose a fully Bayesian approach that treats the kernel hyperparameters as random variables and constructs coupled stochastic differential equations (SDEs) to learn their posterior distribution and that of inducing points. By incorporating estimation uncertainty on hyperparameters, our method enhances the model's flexibility and adaptability to complex dynamics. Additionally, our approach provides a time-varying, comprehensive, and realistic posterior approximation through coupling variables using SDE methods. Experimental results demonstrate the advantages of our method over traditional approaches, showcasing its superior performance in terms of flexibility, accuracy, and other metrics. Our work opens up exciting research avenues for advancing Bayesian inference and offers a powerful modeling tool for continuous-time Gaussian processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge