Flexible Bayesian Last Layer Models Using Implicit Priors and Diffusion Posterior Sampling
Paper and Code
Aug 07, 2024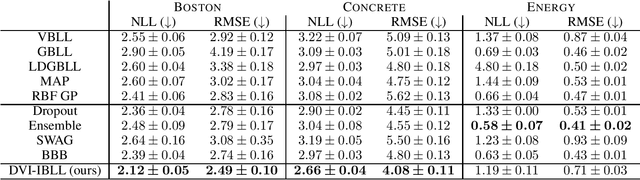
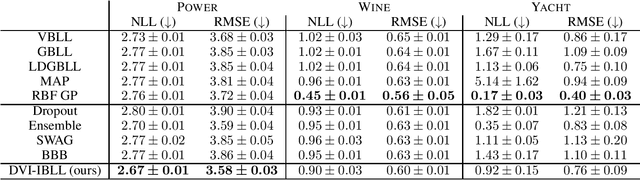
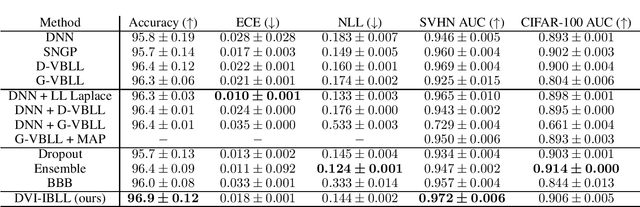
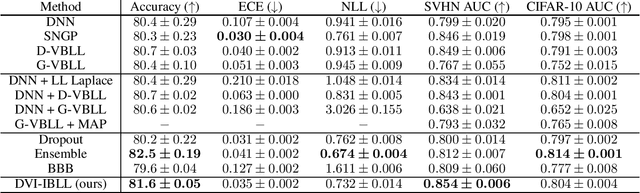
Bayesian Last Layer (BLL) models focus solely on uncertainty in the output layer of neural networks, demonstrating comparable performance to more complex Bayesian models. However, the use of Gaussian priors for last layer weights in Bayesian Last Layer (BLL) models limits their expressive capacity when faced with non-Gaussian, outlier-rich, or high-dimensional datasets. To address this shortfall, we introduce a novel approach that combines diffusion techniques and implicit priors for variational learning of Bayesian last layer weights. This method leverages implicit distributions for modeling weight priors in BLL, coupled with diffusion samplers for approximating true posterior predictions, thereby establishing a comprehensive Bayesian prior and posterior estimation strategy. By delivering an explicit and computationally efficient variational lower bound, our method aims to augment the expressive abilities of BLL models, enhancing model accuracy, calibration, and out-of-distribution detection proficiency. Through detailed exploration and experimental validation, We showcase the method's potential for improving predictive accuracy and uncertainty quantification while ensuring computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge