Sparse Inducing Points in Deep Gaussian Processes: Enhancing Modeling with Denoising Diffusion Variational Inference
Paper and Code
Jul 24, 2024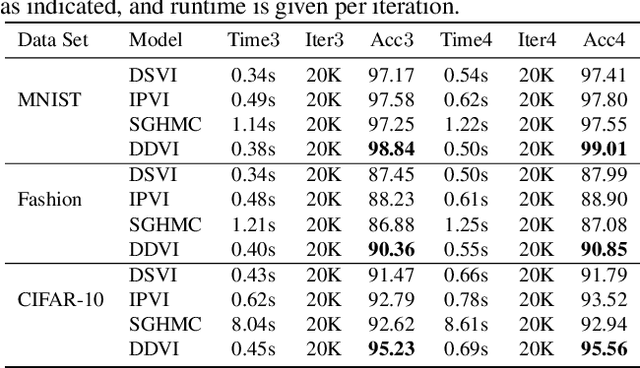
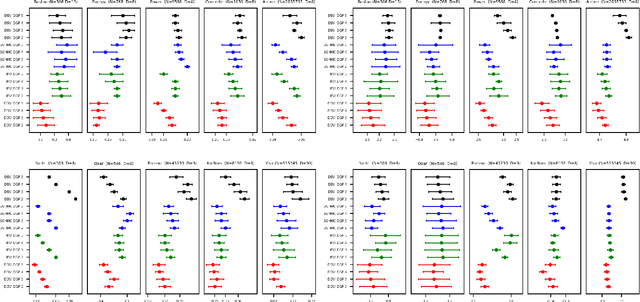
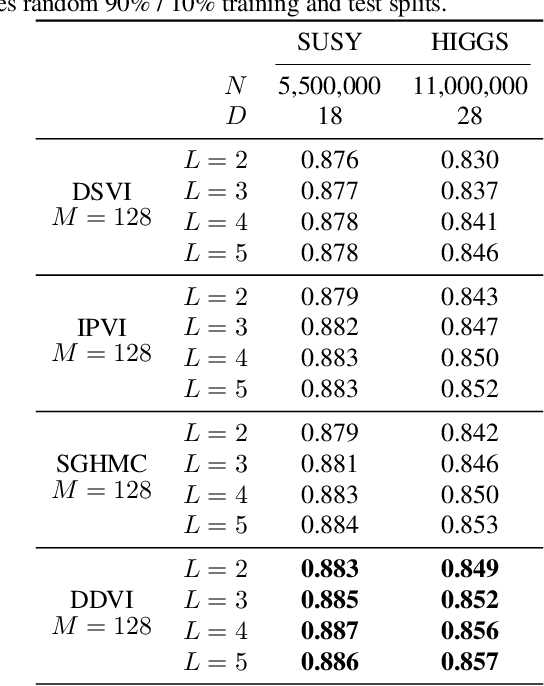

Deep Gaussian processes (DGPs) provide a robust paradigm for Bayesian deep learning. In DGPs, a set of sparse integration locations called inducing points are selected to approximate the posterior distribution of the model. This is done to reduce computational complexity and improve model efficiency. However, inferring the posterior distribution of inducing points is not straightforward. Traditional variational inference approaches to posterior approximation often lead to significant bias. To address this issue, we propose an alternative method called Denoising Diffusion Variational Inference (DDVI) that uses a denoising diffusion stochastic differential equation (SDE) to generate posterior samples of inducing variables. We rely on score matching methods for denoising diffusion model to approximate score functions with a neural network. Furthermore, by combining classical mathematical theory of SDEs with the minimization of KL divergence between the approximate and true processes, we propose a novel explicit variational lower bound for the marginal likelihood function of DGP. Through experiments on various datasets and comparisons with baseline methods, we empirically demonstrate the effectiveness of DDVI for posterior inference of inducing points for DGP models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge