Optimal Dispersion Under Asynchrony

We study the dispersion problem in anonymous port-labeled graphs: $k \leq n$ mobile agents, each with a unique ID and initially located arbitrarily on the nodes of an $n$-node graph with maximum degree $\Delta$, must autonomously relocate so that no node hosts more than one agent. Dispersion serves as a fundamental task in distributed computing of mobile agents, and its complexity stems from key challenges in local coordination under anonymity and limited memory. The goal is to minimize both the time to achieve dispersion and the memory required per agent. It is known that any algorithm requires $\Omega(k)$ time in the worst case, and $\Omega(\log k)$ bits of memory per agent. A recent result [SPAA'25] gives an optimal $O(k)$-time algorithm in the synchronous setting and an $O(k \log k)$-time algorithm in the asynchronous setting, both using $O(\log(k+\Delta))$ bits. In this paper, we close the complexity gap in the asynchronous setting by presenting the first dispersion algorithm that runs in optimal $O(k)$ time using $O(\log(k+\Delta))$ bits of memory per agent. Our solution is based on a novel technique we develop in this paper that constructs a port-one tree in anonymous graphs, which may be of independent interest.

NTIRE 2025 Image Shadow Removal Challenge Report

This work examines the findings of the NTIRE 2025 Shadow Removal Challenge. A total of 306 participants have registered, with 17 teams successfully submitting their solutions during the final evaluation phase. Following the last two editions, this challenge had two evaluation tracks: one focusing on reconstruction fidelity and the other on visual perception through a user study. Both tracks were evaluated with images from the WSRD+ dataset, simulating interactions between self- and cast-shadows with a large number of diverse objects, textures, and materials.

Dispersion is (Almost) Optimal under (A)synchrony

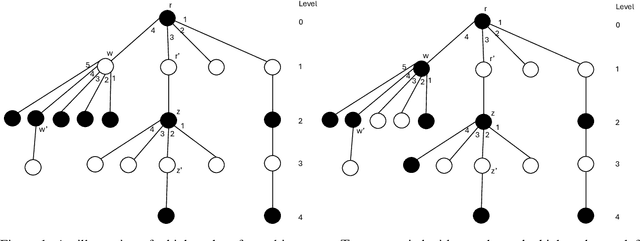
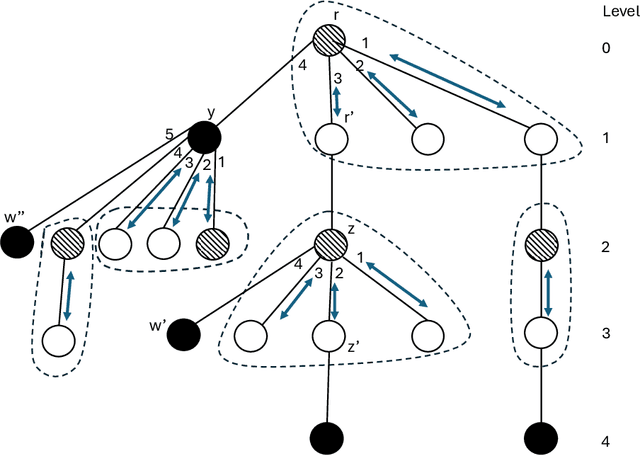
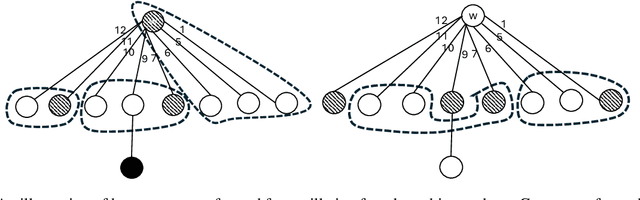
The dispersion problem has received much attention recently in the distributed computing literature. In this problem, $k\leq n$ agents placed initially arbitrarily on the nodes of an $n$-node, $m$-edge anonymous graph of maximum degree $\Delta$ have to reposition autonomously to reach a configuration in which each agent is on a distinct node of the graph. Dispersion is interesting as well as important due to its connections to many fundamental coordination problems by mobile agents on graphs, such as exploration, scattering, load balancing, relocation of self-driven electric cars (robots) to recharge stations (nodes), etc. The objective has been to provide a solution that optimizes simultaneously time and memory complexities. There exist graphs for which the lower bound on time complexity is $\Omega(k)$. Memory complexity is $\Omega(\log k)$ per agent independent of graph topology. The state-of-the-art algorithms have (i) time complexity $O(k\log^2k)$ and memory complexity $O(\log(k+\Delta))$ under the synchronous setting [DISC'24] and (ii) time complexity $O(\min\{m,k\Delta\})$ and memory complexity $O(\log(k+\Delta))$ under the asynchronous setting [OPODIS'21]. In this paper, we improve substantially on this state-of-the-art. Under the synchronous setting as in [DISC'24], we present the first optimal $O(k)$ time algorithm keeping memory complexity $O(\log (k+\Delta))$. Under the asynchronous setting as in [OPODIS'21], we present the first algorithm with time complexity $O(k\log k)$ keeping memory complexity $O(\log (k+\Delta))$, which is time-optimal within an $O(\log k)$ factor despite asynchrony. Both results were obtained through novel techniques to quickly find empty nodes to settle agents, which may be of independent interest.

Hybrid Fingerprint-based Positioning in Cell-Free Massive MIMO Systems

Recently, there has been an increasing interest in 6G technology for integrated sensing and communications, where positioning stands out as a key application. In the realm of 6G, cell-free massive multiple-input multiple-output (MIMO) systems, featuring distributed base stations equipped with a large number of antennas, present an abundant source of angle-of-arrival (AOA) information that could be exploited for positioning applications. In this paper we leverage this AOA information at the base stations using the multiple signal classification (MUSIC) algorithm, in conjunction with received signal strength (RSS) for positioning through Gaussian process regression (GPR). An AOA fingerprint database is constructed by capturing the angle data from multiple locations across the network area and is combined with RSS data from the same locations to form a hybrid fingerprint which is then used to train a GPR model employing a squared exponential kernel. The trained regression model is subsequently utilized to estimate the location of a user equipment. Simulations demonstrate that the GPR model with hybrid input achieves better positioning accuracy than traditional GPR models utilizing RSS-only and AOA-only inputs.

Robot Swarming over the internet

This paper considers cooperative control of robots involving two different testbed systems in remote locations with communication on the internet. This provides us the capability to exchange robots status like positions, velocities and directions needed for the swarming algorithm. The results show that all robots properly follow some leader defined one of the testbeds. Measurement of data exchange rates show no loss of packets, and average transfer delays stay within tolerance limits for practical applications. In our knowledge, the novelty of this paper concerns this kind of control over a large network like internet.

Mambular: A Sequential Model for Tabular Deep Learning

The analysis of tabular data has traditionally been dominated by gradient-boosted decision trees (GBDTs), known for their proficiency with mixed categorical and numerical features. However, recent deep learning innovations are challenging this dominance. We introduce Mambular, an adaptation of the Mamba architecture optimized for tabular data. We extensively benchmark Mambular against state-of-the-art models, including neural networks and tree-based methods, and demonstrate its competitive performance across diverse datasets. Additionally, we explore various adaptations of Mambular to understand its effectiveness for tabular data. We investigate different pooling strategies, feature interaction mechanisms, and bi-directional processing. Our analysis shows that interpreting features as a sequence and passing them through Mamba layers results in surprisingly performant models. The results highlight Mambulars potential as a versatile and powerful architecture for tabular data analysis, expanding the scope of deep learning applications in this domain. The source code is available at https://github.com/basf/mamba-tabular.

Multi Agent Pathfinding for Noise Restricted Hybrid Fuel Unmanned Aerial Vehicles

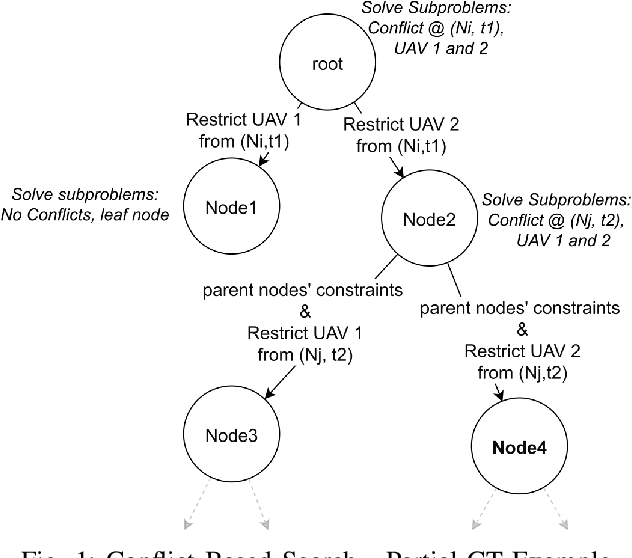
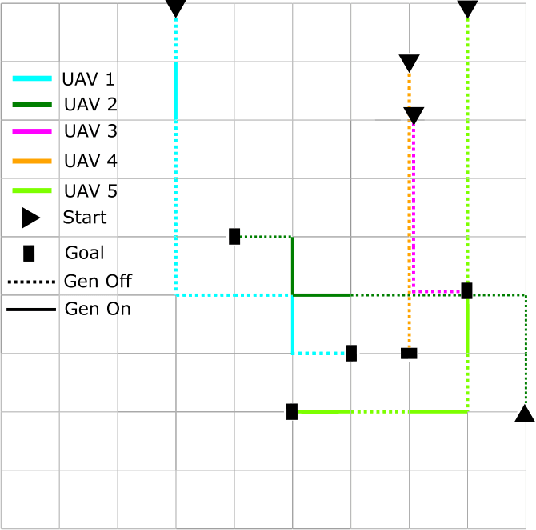
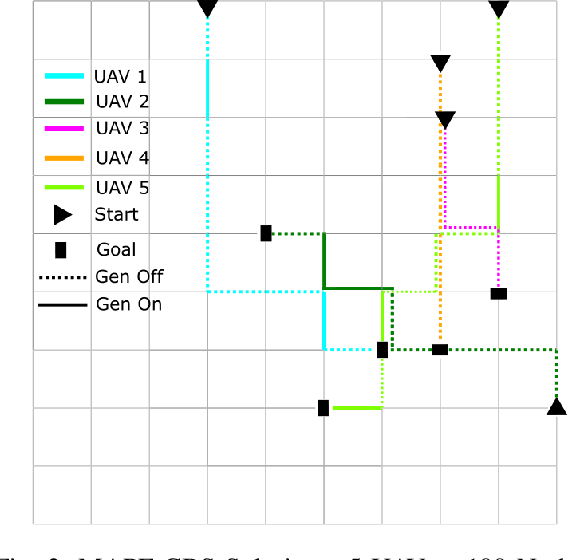
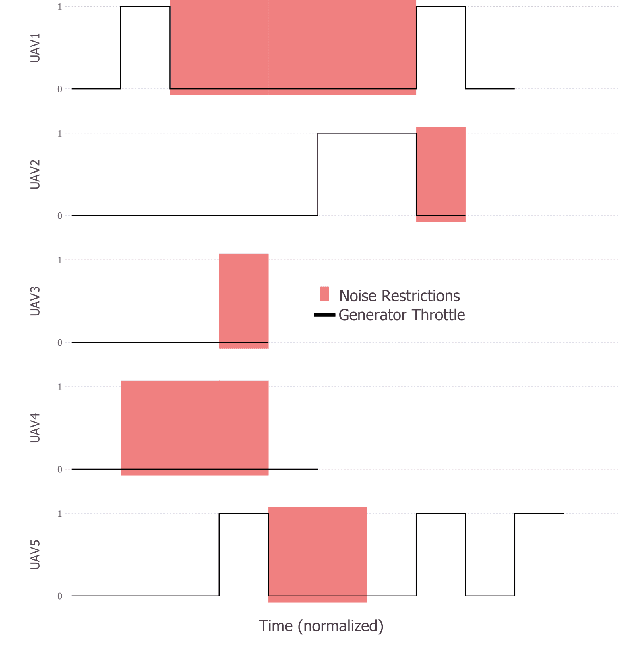
Multi Agent Path Finding (MAPF) seeks the optimal set of paths for multiple agents from respective start to goal locations such that no paths conflict. We address the MAPF problem for a fleet of hybrid-fuel unmanned aerial vehicles which are subject to location-dependent noise restrictions. We solve this problem by searching a constraint tree for which the subproblem at each node is a set of shortest path problems subject to the noise and fuel constraints and conflict zone avoidance. A labeling algorithm is presented to solve this subproblem, including the conflict zones which are treated as dynamic obstacles. We present the experimental results of the algorithms for various graph sizes and number of agents.

A framework of windowed octonion linear canonical transform

The uncertainty principle is a fundamental principle in theoretical physics, such as quantum mechanics and classical mechanics. It plays a prime role in signal processing, including optics, where a signal is to be analyzed simultaneously in both domains; for instance, in harmonic analysis, both time and frequency domains, and in quantum mechanics, both time and momentum. On the other hand, many mathematicians, physicists, and other related domain researchers have paid more attention to the octonion-related integral transforms in recent years. In this paper, we define important properties of the windowed octonion linear canonical transform (WOCLCT), such as inversion, linearity, parity, shifting, and the relationship between OCLCT and WOCLCT. Further, we derived sharp Pitt's and sharp Young-Hausdorff inequalities for 3D WOCLCT. We obtain the logarithmic uncertainty principle for the 3D WOCLCT. Furthermore, Heisenberg's and Donoho-Stark's uncertainty principles are derived for WOCLCT, and the potential applications of WOCLCT are also discussed.

Shape Formation and Locomotion with Joint Movements in the Amoebot Model

We are considering the geometric amoebot model where a set of $n$ amoebots is placed on the triangular grid. An amoebot is able to send information to its neighbors, and to move via expansions and contractions. Since amoebots and information can only travel node by node, most problems have a natural lower bound of $\Omega(D)$ where $D$ denotes the diameter of the structure. Inspired by the nervous and muscular system, Feldmann et al. have proposed the reconfigurable circuit extension and the joint movement extension of the amoebot model with the goal of breaking this lower bound. In the joint movement extension, the way amoebots move is altered. Amoebots become able to push and pull other amoebots. Feldmann et al. demonstrated the power of joint movements by transforming a line of amoebots into a rhombus within $O(\log n)$ rounds. However, they left the details of the extension open. The goal of this paper is therefore to formalize and extend the joint movement extension. In order to provide a proof of concept for the extension, we consider two fundamental problems of modular robot systems: shape formation and locomotion. We approach these problems by defining meta-modules of rhombical and hexagonal shape, respectively. The meta-modules are capable of movement primitives like sliding, rotating, and tunneling. This allows us to simulate shape formation algorithms of various modular robot systems. Finally, we construct three amoebot structures capable of locomotion by rolling, crawling, and walking, respectively.

DeepCPG Policies for Robot Locomotion

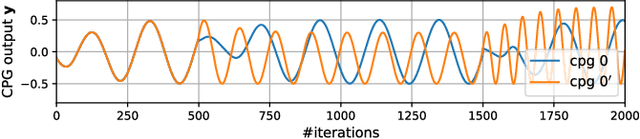
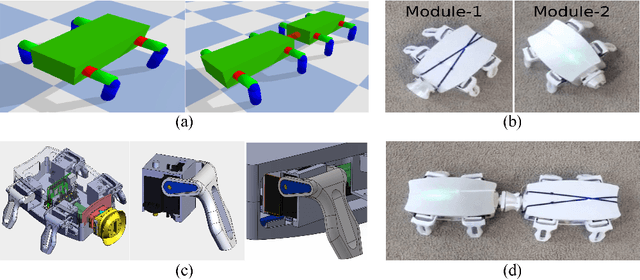
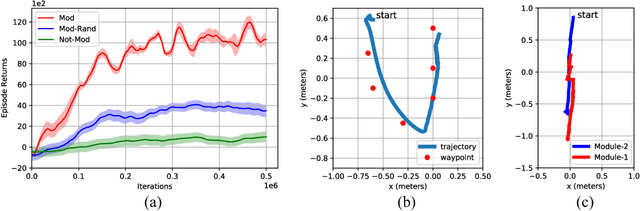
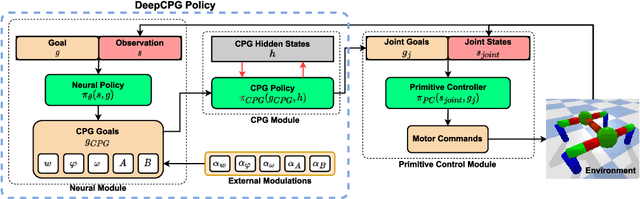
Central Pattern Generators (CPGs) form the neural basis of the observed rhythmic behaviors for locomotion in legged animals. The CPG dynamics organized into networks allow the emergence of complex locomotor behaviors. In this work, we take this inspiration for developing walking behaviors in multi-legged robots. We present novel DeepCPG policies that embed CPGs as a layer in a larger neural network and facilitate end-to-end learning of locomotion behaviors in deep reinforcement learning (DRL) setup. We demonstrate the effectiveness of this approach on physics engine-based insectoid robots. We show that, compared to traditional approaches, DeepCPG policies allow sample-efficient end-to-end learning of effective locomotion strategies even in the case of high-dimensional sensor spaces (vision). We scale the DeepCPG policies using a modular robot configuration and multi-agent DRL. Our results suggest that gradual complexification with embedded priors of these policies in a modular fashion could achieve non-trivial sensor and motor integration on a robot platform. These results also indicate the efficacy of bootstrapping more complex intelligent systems from simpler ones based on biological principles. Finally, we present the experimental results for a proof-of-concept insectoid robot system for which DeepCPG learned policies initially using the simulation engine and these were afterwards transferred to real-world robots without any additional fine-tuning.