Location-Aware Dispersion on Anonymous Graphs

The well-studied DISPERSION problem is a fundamental coordination problem in distributed robotics, where a set of mobile robots must relocate so that each occupies a distinct node of a network. DISPERSION assumes that a robot can settle at any node as long as no other robot settles on that node. In this work, we introduce LOCATION-AWARE DISPERSION, a novel generalization of DISPERSION that incorporates location awareness: Let $G = (V, E)$ be an anonymous, connected, undirected graph with $n = |V|$ nodes, each labeled with a color $\sf{col}(v) \in C = \{c_1, \dots, c_t\}, t\leq n$. A set $R = \{r_1, \dots, r_k\}$ of $k \leq n$ mobile robots is given, where each robot $r_i$ has an associated color $\mathsf{col}(r_i) \in C$. Initially placed arbitrarily on the graph, the goal is to relocate the robots so that each occupies a distinct node of the same color. When $|C|=1$, LOCATION-AWARE DISPERSION reduces to DISPERSION. There is a solution to DISPERSION in graphs with any $k\leq n$ without knowing $k,n$. Like DISPERSION, the goal is to solve LOCATION-AWARE DISPERSION minimizing both time and memory requirement at each agent. We develop several deterministic algorithms with guaranteed bounds on both time and memory requirement. We also give an impossibility and a lower bound for any deterministic algorithm for LOCATION-AWARE DISPERSION. To the best of our knowledge, the presented results collectively establish the algorithmic feasibility of LOCATION-AWARE DISPERSION in anonymous networks and also highlight the challenges on getting an efficient solution compared to the solutions for DISPERSION.

Learning-Augmented Online TRP on a Line

We study the online traveling repairperson problem on a line within the recently proposed learning-augmented framework, which provides predictions on the requests to be served via machine learning. In the original model (with no predictions), there is a stream of requests released over time along the line. The goal is to minimize the sum (or average) of the completion times of the requests. In the original model, the state-of-the-art competitive ratio lower bound is $1+\sqrt{2} > 2.414$ for any deterministic algorithm and the state-of-the-art competitive ratio upper bound is 4 for a deterministic algorithm. Our prediction model involves predicted positions, possibly error-prone, of each request in the stream known a priori but the arrival times of requests are not known until their arrival. We first establish a 3-competitive lower bound which extends to the original model. We then design a deterministic algorithm that is $(2+\sqrt{3})\approx 3.732$-competitive when predictions are perfect. With imperfect predictions (maximum error $δ> 0$), we show that our deterministic algorithm becomes $\min\{3.732+4δ,4\}$-competitive, knowing $δ$. To the best of our knowledge, these are the first results for online traveling repairperson problem in the learning-augmented framework.

Optimal Dispersion Under Asynchrony

We study the dispersion problem in anonymous port-labeled graphs: $k \leq n$ mobile agents, each with a unique ID and initially located arbitrarily on the nodes of an $n$-node graph with maximum degree $\Delta$, must autonomously relocate so that no node hosts more than one agent. Dispersion serves as a fundamental task in distributed computing of mobile agents, and its complexity stems from key challenges in local coordination under anonymity and limited memory. The goal is to minimize both the time to achieve dispersion and the memory required per agent. It is known that any algorithm requires $\Omega(k)$ time in the worst case, and $\Omega(\log k)$ bits of memory per agent. A recent result [SPAA'25] gives an optimal $O(k)$-time algorithm in the synchronous setting and an $O(k \log k)$-time algorithm in the asynchronous setting, both using $O(\log(k+\Delta))$ bits. In this paper, we close the complexity gap in the asynchronous setting by presenting the first dispersion algorithm that runs in optimal $O(k)$ time using $O(\log(k+\Delta))$ bits of memory per agent. Our solution is based on a novel technique we develop in this paper that constructs a port-one tree in anonymous graphs, which may be of independent interest.

Dispersion is (Almost) Optimal under (A)synchrony

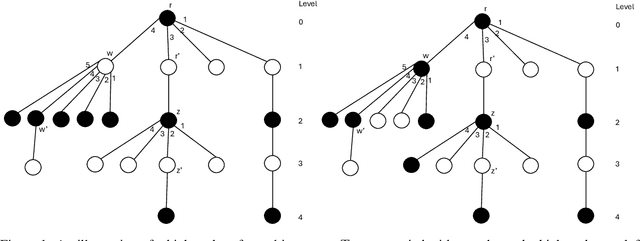
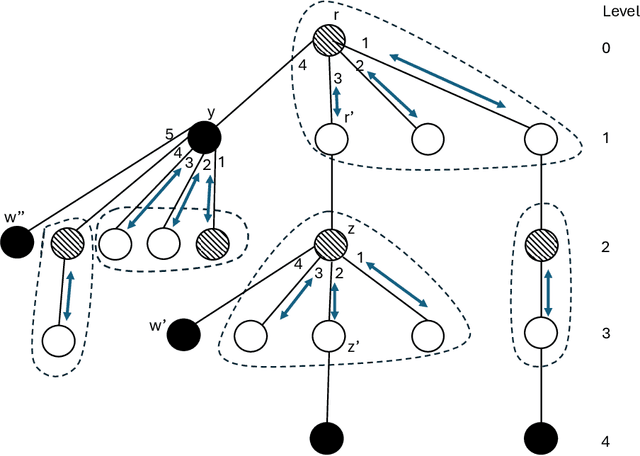
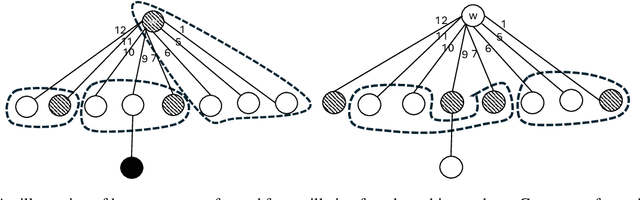
The dispersion problem has received much attention recently in the distributed computing literature. In this problem, $k\leq n$ agents placed initially arbitrarily on the nodes of an $n$-node, $m$-edge anonymous graph of maximum degree $\Delta$ have to reposition autonomously to reach a configuration in which each agent is on a distinct node of the graph. Dispersion is interesting as well as important due to its connections to many fundamental coordination problems by mobile agents on graphs, such as exploration, scattering, load balancing, relocation of self-driven electric cars (robots) to recharge stations (nodes), etc. The objective has been to provide a solution that optimizes simultaneously time and memory complexities. There exist graphs for which the lower bound on time complexity is $\Omega(k)$. Memory complexity is $\Omega(\log k)$ per agent independent of graph topology. The state-of-the-art algorithms have (i) time complexity $O(k\log^2k)$ and memory complexity $O(\log(k+\Delta))$ under the synchronous setting [DISC'24] and (ii) time complexity $O(\min\{m,k\Delta\})$ and memory complexity $O(\log(k+\Delta))$ under the asynchronous setting [OPODIS'21]. In this paper, we improve substantially on this state-of-the-art. Under the synchronous setting as in [DISC'24], we present the first optimal $O(k)$ time algorithm keeping memory complexity $O(\log (k+\Delta))$. Under the asynchronous setting as in [OPODIS'21], we present the first algorithm with time complexity $O(k\log k)$ keeping memory complexity $O(\log (k+\Delta))$, which is time-optimal within an $O(\log k)$ factor despite asynchrony. Both results were obtained through novel techniques to quickly find empty nodes to settle agents, which may be of independent interest.

Deep Recurrent Q-learning for Energy-constrained Coverage with a Mobile Robot

In this paper, we study the problem of coverage of an environment with an energy-constrained robot in the presence of multiple charging stations. As the robot's on-board power supply is limited, it might not have enough energy to cover all the points in the environment with a single charge. Instead, it will need to stop at one or more charging stations to recharge its battery intermittently. The robot cannot violate the energy constraint, i.e., visit a location with negative available energy. To solve this problem, we propose a deep Q-learning framework that produces a policy to maximize the coverage and minimize the budget violations. Our proposed framework also leverages the memory of a recurrent neural network (RNN) to better suit this multi-objective optimization problem. We have tested the presented framework within a 16 x 16 grid environment having charging stations and various obstacle configurations. Results show that our proposed method finds feasible solutions and outperforms a comparable existing technique.

Collisionless Pattern Discovery in Robot Swarms Using Deep Reinforcement Learning

We present a deep reinforcement learning-based framework for automatically discovering patterns available in any given initial configuration of fat robot swarms. In particular, we model the problem of collision-less gathering and mutual visibility in fat robot swarms and discover patterns for solving them using our framework. We show that by shaping reward signals based on certain constraints like mutual visibility and safe proximity, the robots can discover collision-less trajectories leading to well-formed gathering and visibility patterns.

Near-Optimal Dispersion on Arbitrary Anonymous Graphs

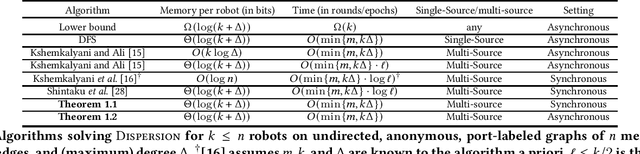
Given an undirected, anonymous, port-labeled graph of $n$ memory-less nodes, $m$ edges, and degree $\Delta$, we consider the problem of dispersing $k\leq n$ robots (or tokens) positioned initially arbitrarily on one or more nodes of the graph to exactly $k$ different nodes of the graph, one on each node. The objective is to simultaneously minimize time to achieve dispersion and memory requirement at each robot. If all $k$ robots are positioned initially on a single node, depth first search (DFS) traversal solves this problem in $O(\min\{m,k\Delta\})$ time with $\Theta(\log(k+\Delta))$ bits at each robot. However, if robots are positioned initially on multiple nodes, the best previously known algorithm solves this problem in $O(\min\{m,k\Delta\}\cdot \log \ell)$ time storing $\Theta(\log(k+\Delta))$ bits at each robot, where $\ell\leq k/2$ is the number of multiplicity nodes in the initial configuration. In this paper, we present a novel multi-source DFS traversal algorithm solving this problem in $O(\min\{m,k\Delta\})$ time with $\Theta(\log(k+\Delta))$ bits at each robot, improving the time bound of the best previously known algorithm by $O(\log \ell)$ and matching asymptotically the single-source DFS traversal bounds. This is the first algorithm for dispersion that is optimal in both time and memory in arbitrary anonymous graphs of constant degree, $\Delta=O(1)$. Furthermore, the result holds in both synchronous and asynchronous settings.

Dispersion of Mobile Robots in the Global Communication Model

The dispersion problem on graphs asks $k\leq n$ robots placed initially arbitrarily on the nodes of an $n$-node anonymous graph to reposition autonomously to reach a configuration in which each robot is on a distinct node of the graph. This problem is of significant interest due to its relationship to other fundamental robot coordination problems, such as exploration, scattering, load balancing etc. In this paper, we consider dispersion in the {\em global communication} model where a robot can communicate with any other robot in the graph (but the graph is unknown to robots). We provide three novel deterministic algorithms, two for arbitrary graphs and one for arbitrary trees, in a synchronous setting where all robots perform their actions in every time step. For arbitrary graphs, our first algorithm is based on a DFS traversal and guarantees $O(\min(m,k\Delta))$ steps runtime using $\Theta(\log (\max(k,\Delta)))$ bits at each robot, where $m$ is the number of edges and $\Delta$ is the maximum degree of the graph. The second algorithm for arbitrary graphs is based on a BFS traversal and guarantees $O( \max(D,k) \Delta (D+\Delta))$ steps runtime using $O(\max(D,\Delta \log k))$ bits at each robot, where $D$ is the diameter of the graph. The algorithm for arbitrary trees is also based on a BFS travesal and guarantees $O(D\max(D,k))$ steps runtime using $O(\max(D,\Delta \log k))$ bits at each robot. Our results are significant improvements compared to the existing results established in the {\em local communication} model where a robot can communication only with other robots present at the same node. Particularly, the DFS-based algorithm is optimal for both memory and time in constant-degree arbitrary graphs. The BFS-based algorithm for arbitrary trees is optimal with respect to runtime when $k\leq O(D)$.

A Constant-Factor Approximation Algorithm for Online Coverage Path Planning with Energy Constraint

In this paper, we study the problem of coverage planning by a mobile robot with a limited energy budget. The objective of the robot is to cover every point in the environment while minimizing the traveled path length. The environment is initially unknown to the robot. Therefore, it needs to avoid the obstacles in the environment on-the-fly during the exploration. As the robot has a specific energy budget, it might not be able to cover the complete environment in one traversal. Instead, it will need to visit a static charging station periodically in order to recharge its energy. To solve the stated problem, we propose a budgeted depth-first search (DFS)-based exploration strategy that helps the robot to cover any unknown planar environment while bounding the maximum path length to a constant-factor of the shortest-possible path length. Our $O(1)$-approximation guarantee advances the state-of-the-art of log-approximation for this problem. Simulation results show that our proposed algorithm outperforms the current state-of-the-art algorithm both in terms of the traveled path length and run time in all the tested environments with concave and convex obstacles.