Optimal Dispersion Under Asynchrony

We study the dispersion problem in anonymous port-labeled graphs: $k \leq n$ mobile agents, each with a unique ID and initially located arbitrarily on the nodes of an $n$-node graph with maximum degree $\Delta$, must autonomously relocate so that no node hosts more than one agent. Dispersion serves as a fundamental task in distributed computing of mobile agents, and its complexity stems from key challenges in local coordination under anonymity and limited memory. The goal is to minimize both the time to achieve dispersion and the memory required per agent. It is known that any algorithm requires $\Omega(k)$ time in the worst case, and $\Omega(\log k)$ bits of memory per agent. A recent result [SPAA'25] gives an optimal $O(k)$-time algorithm in the synchronous setting and an $O(k \log k)$-time algorithm in the asynchronous setting, both using $O(\log(k+\Delta))$ bits. In this paper, we close the complexity gap in the asynchronous setting by presenting the first dispersion algorithm that runs in optimal $O(k)$ time using $O(\log(k+\Delta))$ bits of memory per agent. Our solution is based on a novel technique we develop in this paper that constructs a port-one tree in anonymous graphs, which may be of independent interest.

Dispersion is (Almost) Optimal under (A)synchrony

The dispersion problem has received much attention recently in the distributed computing literature. In this problem, $k\leq n$ agents placed initially arbitrarily on the nodes of an $n$-node, $m$-edge anonymous graph of maximum degree $\Delta$ have to reposition autonomously to reach a configuration in which each agent is on a distinct node of the graph. Dispersion is interesting as well as important due to its connections to many fundamental coordination problems by mobile agents on graphs, such as exploration, scattering, load balancing, relocation of self-driven electric cars (robots) to recharge stations (nodes), etc. The objective has been to provide a solution that optimizes simultaneously time and memory complexities. There exist graphs for which the lower bound on time complexity is $\Omega(k)$. Memory complexity is $\Omega(\log k)$ per agent independent of graph topology. The state-of-the-art algorithms have (i) time complexity $O(k\log^2k)$ and memory complexity $O(\log(k+\Delta))$ under the synchronous setting [DISC'24] and (ii) time complexity $O(\min\{m,k\Delta\})$ and memory complexity $O(\log(k+\Delta))$ under the asynchronous setting [OPODIS'21]. In this paper, we improve substantially on this state-of-the-art. Under the synchronous setting as in [DISC'24], we present the first optimal $O(k)$ time algorithm keeping memory complexity $O(\log (k+\Delta))$. Under the asynchronous setting as in [OPODIS'21], we present the first algorithm with time complexity $O(k\log k)$ keeping memory complexity $O(\log (k+\Delta))$, which is time-optimal within an $O(\log k)$ factor despite asynchrony. Both results were obtained through novel techniques to quickly find empty nodes to settle agents, which may be of independent interest.

Near-Optimal Dispersion on Arbitrary Anonymous Graphs

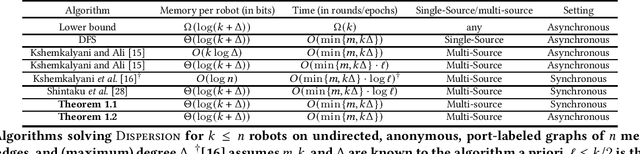
Given an undirected, anonymous, port-labeled graph of $n$ memory-less nodes, $m$ edges, and degree $\Delta$, we consider the problem of dispersing $k\leq n$ robots (or tokens) positioned initially arbitrarily on one or more nodes of the graph to exactly $k$ different nodes of the graph, one on each node. The objective is to simultaneously minimize time to achieve dispersion and memory requirement at each robot. If all $k$ robots are positioned initially on a single node, depth first search (DFS) traversal solves this problem in $O(\min\{m,k\Delta\})$ time with $\Theta(\log(k+\Delta))$ bits at each robot. However, if robots are positioned initially on multiple nodes, the best previously known algorithm solves this problem in $O(\min\{m,k\Delta\}\cdot \log \ell)$ time storing $\Theta(\log(k+\Delta))$ bits at each robot, where $\ell\leq k/2$ is the number of multiplicity nodes in the initial configuration. In this paper, we present a novel multi-source DFS traversal algorithm solving this problem in $O(\min\{m,k\Delta\})$ time with $\Theta(\log(k+\Delta))$ bits at each robot, improving the time bound of the best previously known algorithm by $O(\log \ell)$ and matching asymptotically the single-source DFS traversal bounds. This is the first algorithm for dispersion that is optimal in both time and memory in arbitrary anonymous graphs of constant degree, $\Delta=O(1)$. Furthermore, the result holds in both synchronous and asynchronous settings.

Dispersion of Mobile Robots in the Global Communication Model

The dispersion problem on graphs asks $k\leq n$ robots placed initially arbitrarily on the nodes of an $n$-node anonymous graph to reposition autonomously to reach a configuration in which each robot is on a distinct node of the graph. This problem is of significant interest due to its relationship to other fundamental robot coordination problems, such as exploration, scattering, load balancing etc. In this paper, we consider dispersion in the {\em global communication} model where a robot can communicate with any other robot in the graph (but the graph is unknown to robots). We provide three novel deterministic algorithms, two for arbitrary graphs and one for arbitrary trees, in a synchronous setting where all robots perform their actions in every time step. For arbitrary graphs, our first algorithm is based on a DFS traversal and guarantees $O(\min(m,k\Delta))$ steps runtime using $\Theta(\log (\max(k,\Delta)))$ bits at each robot, where $m$ is the number of edges and $\Delta$ is the maximum degree of the graph. The second algorithm for arbitrary graphs is based on a BFS traversal and guarantees $O( \max(D,k) \Delta (D+\Delta))$ steps runtime using $O(\max(D,\Delta \log k))$ bits at each robot, where $D$ is the diameter of the graph. The algorithm for arbitrary trees is also based on a BFS travesal and guarantees $O(D\max(D,k))$ steps runtime using $O(\max(D,\Delta \log k))$ bits at each robot. Our results are significant improvements compared to the existing results established in the {\em local communication} model where a robot can communication only with other robots present at the same node. Particularly, the DFS-based algorithm is optimal for both memory and time in constant-degree arbitrary graphs. The BFS-based algorithm for arbitrary trees is optimal with respect to runtime when $k\leq O(D)$.