Near-Optimal Dispersion on Arbitrary Anonymous Graphs
Paper and Code
Jun 07, 2021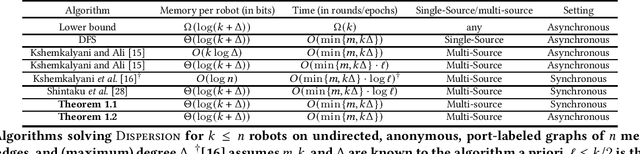
Given an undirected, anonymous, port-labeled graph of $n$ memory-less nodes, $m$ edges, and degree $\Delta$, we consider the problem of dispersing $k\leq n$ robots (or tokens) positioned initially arbitrarily on one or more nodes of the graph to exactly $k$ different nodes of the graph, one on each node. The objective is to simultaneously minimize time to achieve dispersion and memory requirement at each robot. If all $k$ robots are positioned initially on a single node, depth first search (DFS) traversal solves this problem in $O(\min\{m,k\Delta\})$ time with $\Theta(\log(k+\Delta))$ bits at each robot. However, if robots are positioned initially on multiple nodes, the best previously known algorithm solves this problem in $O(\min\{m,k\Delta\}\cdot \log \ell)$ time storing $\Theta(\log(k+\Delta))$ bits at each robot, where $\ell\leq k/2$ is the number of multiplicity nodes in the initial configuration. In this paper, we present a novel multi-source DFS traversal algorithm solving this problem in $O(\min\{m,k\Delta\})$ time with $\Theta(\log(k+\Delta))$ bits at each robot, improving the time bound of the best previously known algorithm by $O(\log \ell)$ and matching asymptotically the single-source DFS traversal bounds. This is the first algorithm for dispersion that is optimal in both time and memory in arbitrary anonymous graphs of constant degree, $\Delta=O(1)$. Furthermore, the result holds in both synchronous and asynchronous settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge