Dispersion is (Almost) Optimal under (A)synchrony
Paper and Code
Mar 20, 2025
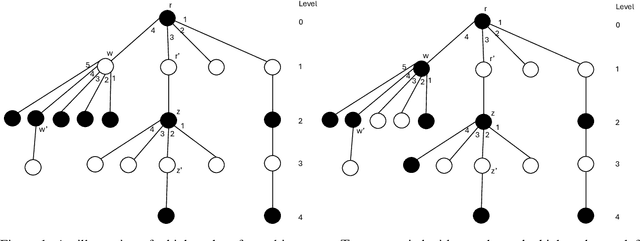
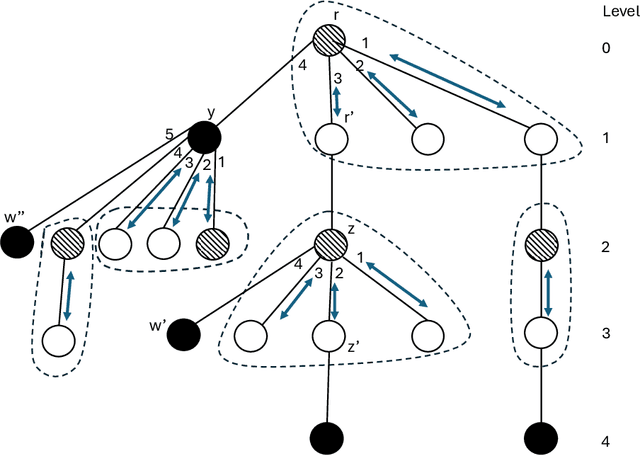
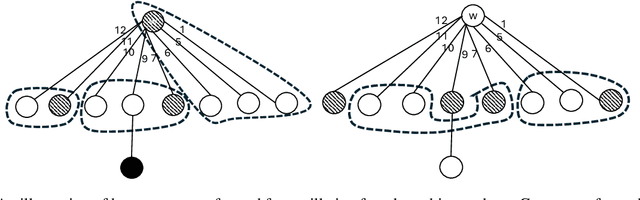
The dispersion problem has received much attention recently in the distributed computing literature. In this problem, $k\leq n$ agents placed initially arbitrarily on the nodes of an $n$-node, $m$-edge anonymous graph of maximum degree $\Delta$ have to reposition autonomously to reach a configuration in which each agent is on a distinct node of the graph. Dispersion is interesting as well as important due to its connections to many fundamental coordination problems by mobile agents on graphs, such as exploration, scattering, load balancing, relocation of self-driven electric cars (robots) to recharge stations (nodes), etc. The objective has been to provide a solution that optimizes simultaneously time and memory complexities. There exist graphs for which the lower bound on time complexity is $\Omega(k)$. Memory complexity is $\Omega(\log k)$ per agent independent of graph topology. The state-of-the-art algorithms have (i) time complexity $O(k\log^2k)$ and memory complexity $O(\log(k+\Delta))$ under the synchronous setting [DISC'24] and (ii) time complexity $O(\min\{m,k\Delta\})$ and memory complexity $O(\log(k+\Delta))$ under the asynchronous setting [OPODIS'21]. In this paper, we improve substantially on this state-of-the-art. Under the synchronous setting as in [DISC'24], we present the first optimal $O(k)$ time algorithm keeping memory complexity $O(\log (k+\Delta))$. Under the asynchronous setting as in [OPODIS'21], we present the first algorithm with time complexity $O(k\log k)$ keeping memory complexity $O(\log (k+\Delta))$, which is time-optimal within an $O(\log k)$ factor despite asynchrony. Both results were obtained through novel techniques to quickly find empty nodes to settle agents, which may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge