EMMA: End-to-End Multimodal Model for Autonomous Driving

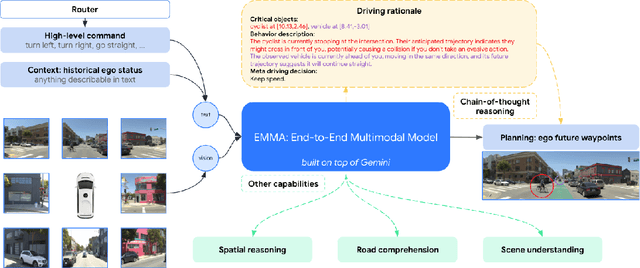
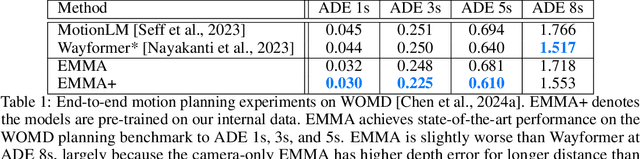
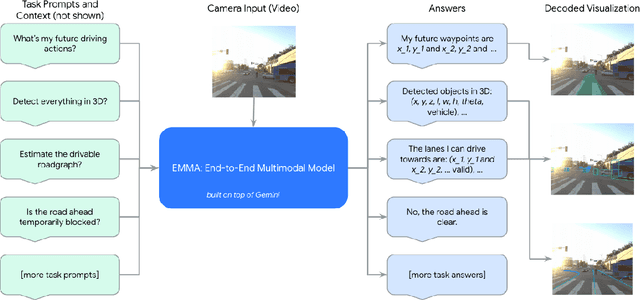
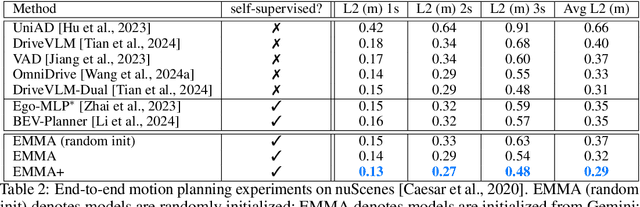
We introduce EMMA, an End-to-end Multimodal Model for Autonomous driving. Built on a multi-modal large language model foundation, EMMA directly maps raw camera sensor data into various driving-specific outputs, including planner trajectories, perception objects, and road graph elements. EMMA maximizes the utility of world knowledge from the pre-trained large language models, by representing all non-sensor inputs (e.g. navigation instructions and ego vehicle status) and outputs (e.g. trajectories and 3D locations) as natural language text. This approach allows EMMA to jointly process various driving tasks in a unified language space, and generate the outputs for each task using task-specific prompts. Empirically, we demonstrate EMMA's effectiveness by achieving state-of-the-art performance in motion planning on nuScenes as well as competitive results on the Waymo Open Motion Dataset (WOMD). EMMA also yields competitive results for camera-primary 3D object detection on the Waymo Open Dataset (WOD). We show that co-training EMMA with planner trajectories, object detection, and road graph tasks yields improvements across all three domains, highlighting EMMA's potential as a generalist model for autonomous driving applications. However, EMMA also exhibits certain limitations: it can process only a small amount of image frames, does not incorporate accurate 3D sensing modalities like LiDAR or radar and is computationally expensive. We hope that our results will inspire further research to mitigate these issues and to further evolve the state of the art in autonomous driving model architectures.

Concrete Score Matching: Generalized Score Matching for Discrete Data

Representing probability distributions by the gradient of their density functions has proven effective in modeling a wide range of continuous data modalities. However, this representation is not applicable in discrete domains where the gradient is undefined. To this end, we propose an analogous score function called the "Concrete score", a generalization of the (Stein) score for discrete settings. Given a predefined neighborhood structure, the Concrete score of any input is defined by the rate of change of the probabilities with respect to local directional changes of the input. This formulation allows us to recover the (Stein) score in continuous domains when measuring such changes by the Euclidean distance, while using the Manhattan distance leads to our novel score function in discrete domains. Finally, we introduce a new framework to learn such scores from samples called Concrete Score Matching (CSM), and propose an efficient training objective to scale our approach to high dimensions. Empirically, we demonstrate the efficacy of CSM on density estimation tasks on a mixture of synthetic, tabular, and high-dimensional image datasets, and demonstrate that it performs favorably relative to existing baselines for modeling discrete data.

LMPriors: Pre-Trained Language Models as Task-Specific Priors

Particularly in low-data regimes, an outstanding challenge in machine learning is developing principled techniques for augmenting our models with suitable priors. This is to encourage them to learn in ways that are compatible with our understanding of the world. But in contrast to generic priors such as shrinkage or sparsity, we draw inspiration from the recent successes of large-scale language models (LMs) to construct task-specific priors distilled from the rich knowledge of LMs. Our method, Language Model Priors (LMPriors), incorporates auxiliary natural language metadata about the task -- such as variable names and descriptions -- to encourage downstream model outputs to be consistent with the LM's common-sense reasoning based on the metadata. Empirically, we demonstrate that LMPriors improve model performance in settings where such natural language descriptions are available, and perform well on several tasks that benefit from such prior knowledge, such as feature selection, causal inference, and safe reinforcement learning.

ButterflyFlow: Building Invertible Layers with Butterfly Matrices

Normalizing flows model complex probability distributions using maps obtained by composing invertible layers. Special linear layers such as masked and 1x1 convolutions play a key role in existing architectures because they increase expressive power while having tractable Jacobians and inverses. We propose a new family of invertible linear layers based on butterfly layers, which are known to theoretically capture complex linear structures including permutations and periodicity, yet can be inverted efficiently. This representational power is a key advantage of our approach, as such structures are common in many real-world datasets. Based on our invertible butterfly layers, we construct a new class of normalizing flow models called ButterflyFlow. Empirically, we demonstrate that ButterflyFlows not only achieve strong density estimation results on natural images such as MNIST, CIFAR-10, and ImageNet 32x32, but also obtain significantly better log-likelihoods on structured datasets such as galaxy images and MIMIC-III patient cohorts -- all while being more efficient in terms of memory and computation than relevant baselines.

Counterbalancing Teacher: Regularizing Batch Normalized Models for Robustness

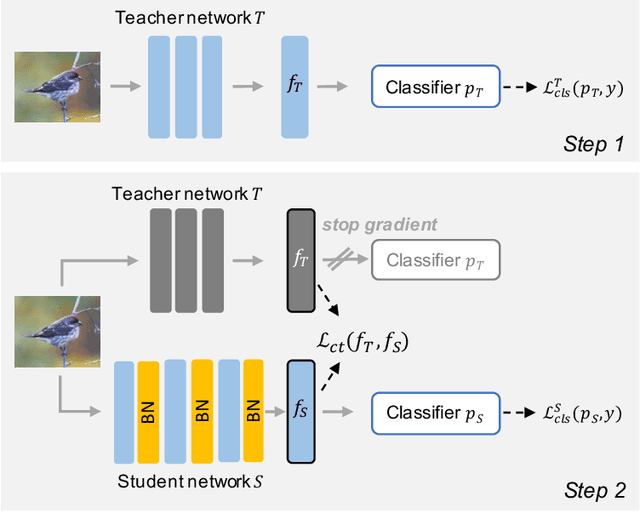
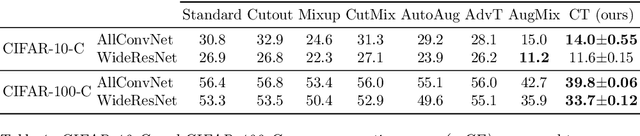
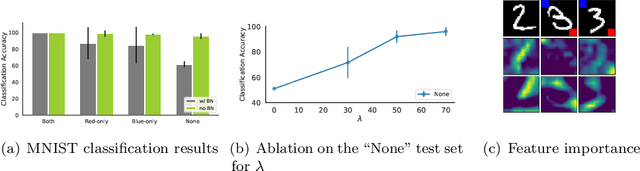
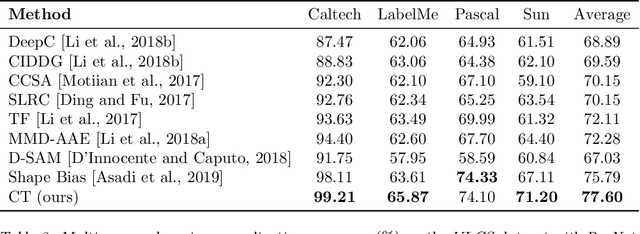
Batch normalization (BN) is a ubiquitous technique for training deep neural networks that accelerates their convergence to reach higher accuracy. However, we demonstrate that BN comes with a fundamental drawback: it incentivizes the model to rely on low-variance features that are highly specific to the training (in-domain) data, hurting generalization performance on out-of-domain examples. In this work, we investigate this phenomenon by first showing that removing BN layers across a wide range of architectures leads to lower out-of-domain and corruption errors at the cost of higher in-domain errors. We then propose Counterbalancing Teacher (CT), a method which leverages a frozen copy of the same model without BN as a teacher to enforce the student network's learning of robust representations by substantially adapting its weights through a consistency loss function. This regularization signal helps CT perform well in unforeseen data shifts, even without information from the target domain as in prior works. We theoretically show in an overparameterized linear regression setting why normalization leads to a model's reliance on such in-domain features, and empirically demonstrate the efficacy of CT by outperforming several baselines on robustness benchmarks such as CIFAR-10-C, CIFAR-100-C, and VLCS.

Density Ratio Estimation via Infinitesimal Classification

Density ratio estimation (DRE) is a fundamental machine learning technique for comparing two probability distributions. However, existing methods struggle in high-dimensional settings, as it is difficult to accurately compare probability distributions based on finite samples. In this work we propose DRE-\infty, a divide-and-conquer approach to reduce DRE to a series of easier subproblems. Inspired by Monte Carlo methods, we smoothly interpolate between the two distributions via an infinite continuum of intermediate bridge distributions. We then estimate the instantaneous rate of change of the bridge distributions indexed by time (the "time score") -- a quantity defined analogously to data (Stein) scores -- with a novel time score matching objective. Crucially, the learned time scores can then be integrated to compute the desired density ratio. In addition, we show that traditional (Stein) scores can be used to obtain integration paths that connect regions of high density in both distributions, improving performance in practice. Empirically, we demonstrate that our approach performs well on downstream tasks such as mutual information estimation and energy-based modeling on complex, high-dimensional datasets.

Featurized Density Ratio Estimation

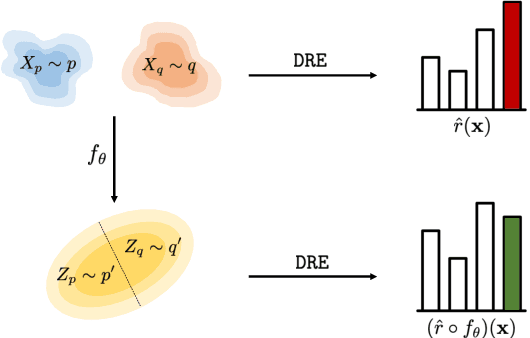
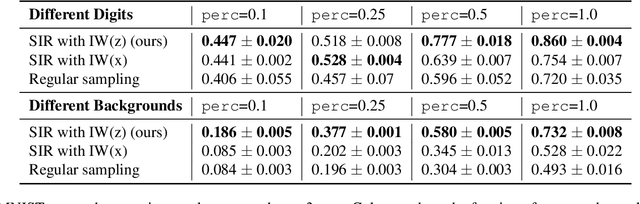
Density ratio estimation serves as an important technique in the unsupervised machine learning toolbox. However, such ratios are difficult to estimate for complex, high-dimensional data, particularly when the densities of interest are sufficiently different. In our work, we propose to leverage an invertible generative model to map the two distributions into a common feature space prior to estimation. This featurization brings the densities closer together in latent space, sidestepping pathological scenarios where the learned density ratios in input space can be arbitrarily inaccurate. At the same time, the invertibility of our feature map guarantees that the ratios computed in feature space are equivalent to those in input space. Empirically, we demonstrate the efficacy of our approach in a variety of downstream tasks that require access to accurate density ratios such as mutual information estimation, targeted sampling in deep generative models, and classification with data augmentation.

Robust Representation Learning via Perceptual Similarity Metrics

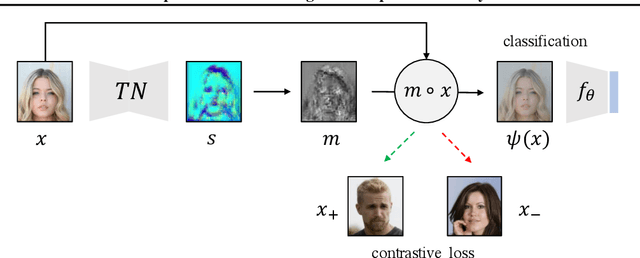
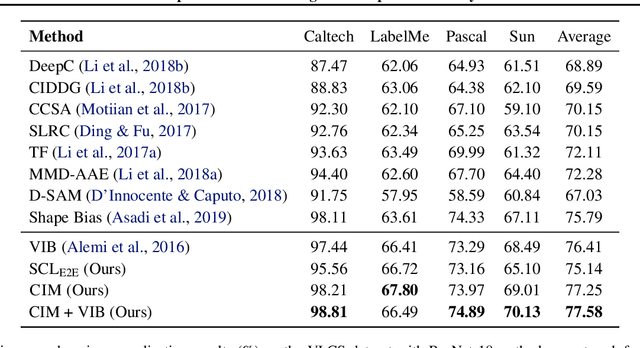
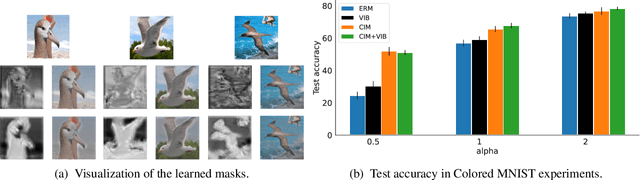
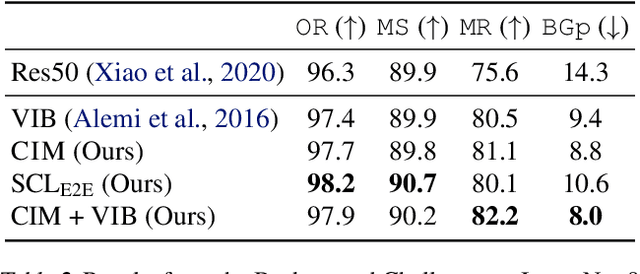
A fundamental challenge in artificial intelligence is learning useful representations of data that yield good performance on a downstream task, without overfitting to spurious input features. Extracting such task-relevant predictive information is particularly difficult for real-world datasets. In this work, we propose Contrastive Input Morphing (CIM), a representation learning framework that learns input-space transformations of the data to mitigate the effect of irrelevant input features on downstream performance. Our method leverages a perceptual similarity metric via a triplet loss to ensure that the transformation preserves task-relevant information.Empirically, we demonstrate the efficacy of our approach on tasks which typically suffer from the presence of spurious correlations: classification with nuisance information, out-of-distribution generalization, and preservation of subgroup accuracies. We additionally show that CIM is complementary to other mutual information-based representation learning techniques, and demonstrate that it improves the performance of variational information bottleneck (VIB) when used together.

Neural Network Compression for Noisy Storage Devices

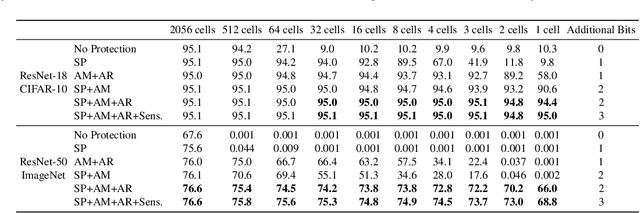
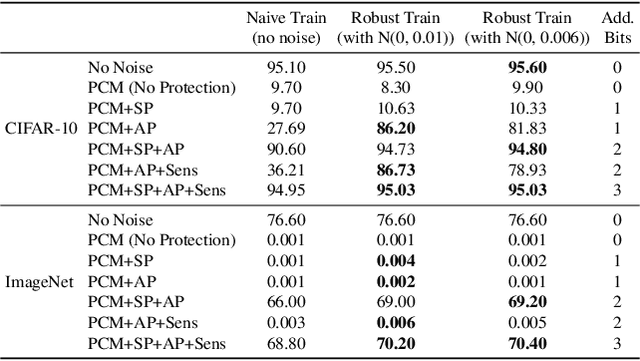
Compression and efficient storage of neural network (NN) parameters is critical for applications that run on resource-constrained devices. Although NN model compression has made significant progress, there has been considerably less investigation in the actual physical storage of NN parameters. Conventionally, model compression and physical storage are decoupled, as digital storage media with error correcting codes (ECCs) provide robust error-free storage. This decoupled approach is inefficient, as it forces the storage to treat each bit of the compressed model equally, and to dedicate the same amount of resources to each bit. We propose a radically different approach that: (i) employs analog memories to maximize the capacity of each memory cell, and (ii) jointly optimizes model compression and physical storage to maximize memory utility. We investigate the challenges of analog storage by studying model storage on phase change memory (PCM) arrays and develop a variety of robust coding strategies for NN model storage. We demonstrate the efficacy of our approach on MNIST, CIFAR-10 and ImageNet datasets for both existing and novel compression methods. Compared to conventional error-free digital storage, our method has the potential to reduce the memory size by one order of magnitude, without significantly compromising the stored model's accuracy.

Encoding Musical Style with Transformer Autoencoders

We consider the problem of learning high-level controls over the global structure of sequence generation, particularly in the context of symbolic music generation with complex language models. In this work, we present the Transformer autoencoder, which aggregates encodings of the input data across time to obtain a global representation of style from a given performance. We show it is possible to combine this global embedding with other temporally distributed embeddings, enabling improved control over the separate aspects of performance style and and melody. Empirically, we demonstrate the effectiveness of our method on a variety of music generation tasks on the MAESTRO dataset and a YouTube dataset with 10,000+ hours of piano performances, where we achieve improvements in terms of log-likelihood and mean listening scores as compared to relevant baselines.