Dongwoo Kim
KAIST
In-Place Feedback: A New Paradigm for Guiding LLMs in Multi-Turn Reasoning
Oct 01, 2025Abstract:Large language models (LLMs) are increasingly studied in the context of multi-turn reasoning, where models iteratively refine their outputs based on user-provided feedback. Such settings are crucial for tasks that require complex reasoning, yet existing feedback paradigms often rely on issuing new messages. LLMs struggle to integrate these reliably, leading to inconsistent improvements. In this work, we introduce in-place feedback, a novel interaction paradigm in which users directly edit an LLM's previous response, and the model conditions on this modified response to generate its revision. Empirical evaluations on diverse reasoning-intensive benchmarks reveal that in-place feedback achieves better performance than conventional multi-turn feedback while using $79.1\%$ fewer tokens. Complementary analyses on controlled environments further demonstrate that in-place feedback resolves a core limitation of multi-turn feedback: models often fail to apply feedback precisely to erroneous parts of the response, leaving errors uncorrected and sometimes introducing new mistakes into previously correct content. These findings suggest that in-place feedback offers a more natural and effective mechanism for guiding LLMs in reasoning-intensive tasks.
Delving into Instance-Dependent Label Noise in Graph Data: A Comprehensive Study and Benchmark
Jun 14, 2025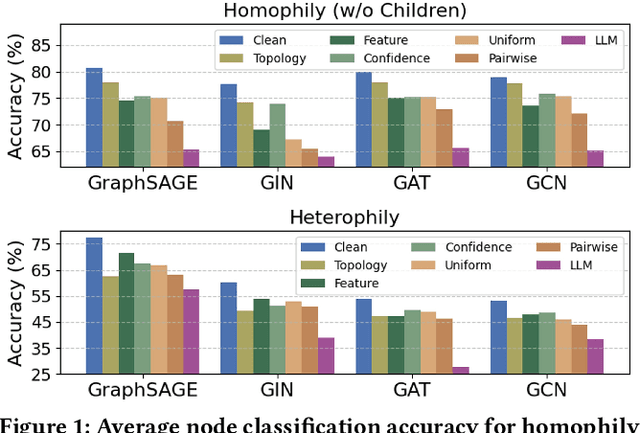
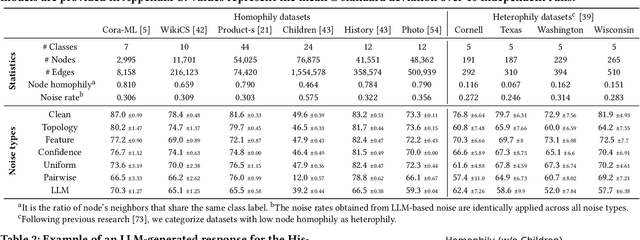
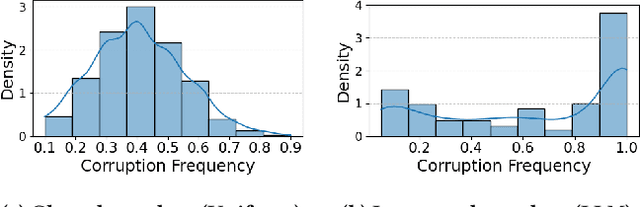
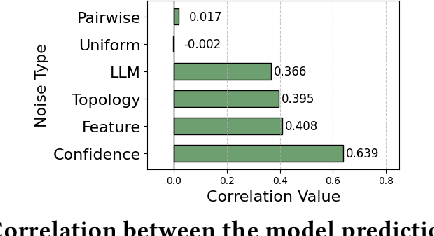
Abstract:Graph Neural Networks (GNNs) have achieved state-of-the-art performance in node classification tasks but struggle with label noise in real-world data. Existing studies on graph learning with label noise commonly rely on class-dependent label noise, overlooking the complexities of instance-dependent noise and falling short of capturing real-world corruption patterns. We introduce BeGIN (Benchmarking for Graphs with Instance-dependent Noise), a new benchmark that provides realistic graph datasets with various noise types and comprehensively evaluates noise-handling strategies across GNN architectures, noisy label detection, and noise-robust learning. To simulate instance-dependent corruptions, BeGIN introduces algorithmic methods and LLM-based simulations. Our experiments reveal the challenges of instance-dependent noise, particularly LLM-based corruption, and underscore the importance of node-specific parameterization to enhance GNN robustness. By comprehensively evaluating noise-handling strategies, BeGIN provides insights into their effectiveness, efficiency, and key performance factors. We expect that BeGIN will serve as a valuable resource for advancing research on label noise in graphs and fostering the development of robust GNN training methods. The code is available at https://github.com/kimsu55/BeGIN.
* 17 pages
The Oversmoothing Fallacy: A Misguided Narrative in GNN Research
Jun 05, 2025Abstract:Oversmoothing has been recognized as a main obstacle to building deep Graph Neural Networks (GNNs), limiting the performance. This position paper argues that the influence of oversmoothing has been overstated and advocates for a further exploration of deep GNN architectures. Given the three core operations of GNNs, aggregation, linear transformation, and non-linear activation, we show that prior studies have mistakenly confused oversmoothing with the vanishing gradient, caused by transformation and activation rather than aggregation. Our finding challenges prior beliefs about oversmoothing being unique to GNNs. Furthermore, we demonstrate that classical solutions such as skip connections and normalization enable the successful stacking of deep GNN layers without performance degradation. Our results clarify misconceptions about oversmoothing and shed new light on the potential of deep GNNs.
Influence Functions for Edge Edits in Non-Convex Graph Neural Networks
Jun 05, 2025Abstract:Understanding how individual edges influence the behavior of graph neural networks (GNNs) is essential for improving their interpretability and robustness. Graph influence functions have emerged as promising tools to efficiently estimate the effects of edge deletions without retraining. However, existing influence prediction methods rely on strict convexity assumptions, exclusively consider the influence of edge deletions while disregarding edge insertions, and fail to capture changes in message propagation caused by these modifications. In this work, we propose a proximal Bregman response function specifically tailored for GNNs, relaxing the convexity requirement and enabling accurate influence prediction for standard neural network architectures. Furthermore, our method explicitly accounts for message propagation effects and extends influence prediction to both edge deletions and insertions in a principled way. Experiments with real-world datasets demonstrate accurate influence predictions for different characteristics of GNNs. We further demonstrate that the influence function is versatile in applications such as graph rewiring and adversarial attacks.
High-order Equivariant Flow Matching for Density Functional Theory Hamiltonian Prediction
May 24, 2025Abstract:Density functional theory (DFT) is a fundamental method for simulating quantum chemical properties, but it remains expensive due to the iterative self-consistent field (SCF) process required to solve the Kohn-Sham equations. Recently, deep learning methods are gaining attention as a way to bypass this step by directly predicting the Hamiltonian. However, they rely on deterministic regression and do not consider the highly structured nature of Hamiltonians. In this work, we propose QHFlow, a high-order equivariant flow matching framework that generates Hamiltonian matrices conditioned on molecular geometry. Flow matching models continuous-time trajectories between simple priors and complex targets, learning the structured distributions over Hamiltonians instead of direct regression. To further incorporate symmetry, we use a neural architecture that predicts SE(3)-equivariant vector fields, improving accuracy and generalization across diverse geometries. To further enhance physical fidelity, we additionally introduce a fine-tuning scheme to align predicted orbital energies with the target. QHFlow achieves state-of-the-art performance, reducing Hamiltonian error by 71% on MD17 and 53% on QH9. Moreover, we further show that QHFlow accelerates the DFT process without trading off the solution quality when initializing SCF iterations with the predicted Hamiltonian, significantly reducing the number of iterations and runtime.
Plane Geometry Problem Solving with Multi-modal Reasoning: A Survey
May 20, 2025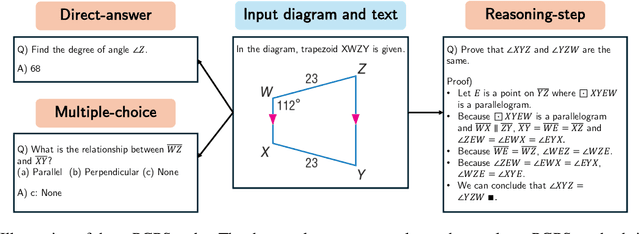
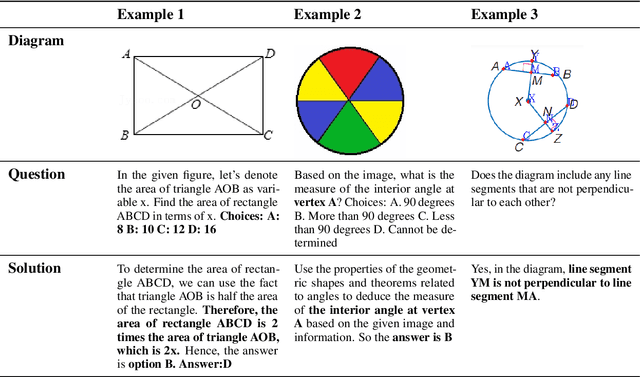
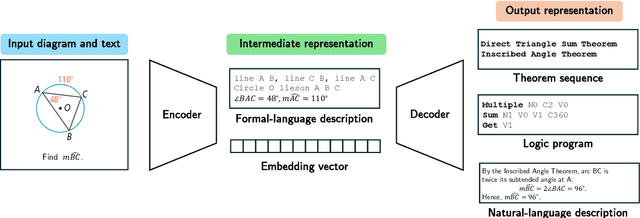
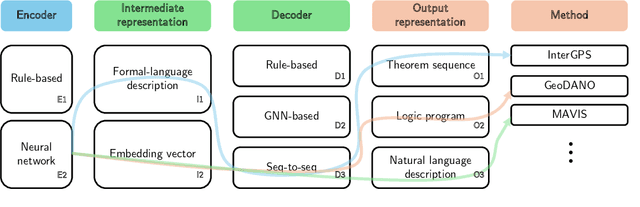
Abstract:Plane geometry problem solving (PGPS) has recently gained significant attention as a benchmark to assess the multi-modal reasoning capabilities of large vision-language models. Despite the growing interest in PGPS, the research community still lacks a comprehensive overview that systematically synthesizes recent work in PGPS. To fill this gap, we present a survey of existing PGPS studies. We first categorize PGPS methods into an encoder-decoder framework and summarize the corresponding output formats used by their encoders and decoders. Subsequently, we classify and analyze these encoders and decoders according to their architectural designs. Finally, we outline major challenges and promising directions for future research. In particular, we discuss the hallucination issues arising during the encoding phase within encoder-decoder architectures, as well as the problem of data leakage in current PGPS benchmarks.
Phi-4-Mini Technical Report: Compact yet Powerful Multimodal Language Models via Mixture-of-LoRAs
Mar 03, 2025



Abstract:We introduce Phi-4-Mini and Phi-4-Multimodal, compact yet highly capable language and multimodal models. Phi-4-Mini is a 3.8-billion-parameter language model trained on high-quality web and synthetic data, significantly outperforming recent open-source models of similar size and matching the performance of models twice its size on math and coding tasks requiring complex reasoning. This achievement is driven by a carefully curated synthetic data recipe emphasizing high-quality math and coding datasets. Compared to its predecessor, Phi-3.5-Mini, Phi-4-Mini features an expanded vocabulary size of 200K tokens to better support multilingual applications, as well as group query attention for more efficient long-sequence generation. Phi-4-Multimodal is a multimodal model that integrates text, vision, and speech/audio input modalities into a single model. Its novel modality extension approach leverages LoRA adapters and modality-specific routers to allow multiple inference modes combining various modalities without interference. For example, it now ranks first in the OpenASR leaderboard to date, although the LoRA component of the speech/audio modality has just 460 million parameters. Phi-4-Multimodal supports scenarios involving (vision + language), (vision + speech), and (speech/audio) inputs, outperforming larger vision-language and speech-language models on a wide range of tasks. Additionally, we experiment to further train Phi-4-Mini to enhance its reasoning capabilities. Despite its compact 3.8-billion-parameter size, this experimental version achieves reasoning performance on par with or surpassing significantly larger models, including DeepSeek-R1-Distill-Qwen-7B and DeepSeek-R1-Distill-Llama-8B.
CoPL: Collaborative Preference Learning for Personalizing LLMs
Mar 03, 2025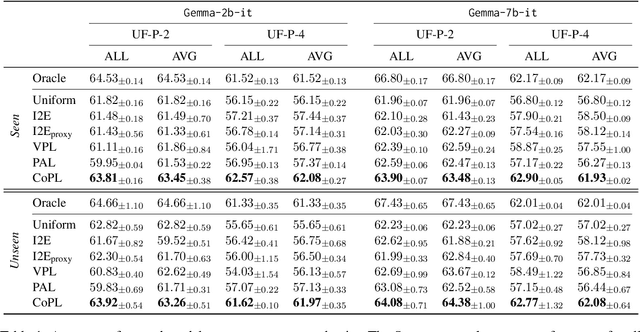


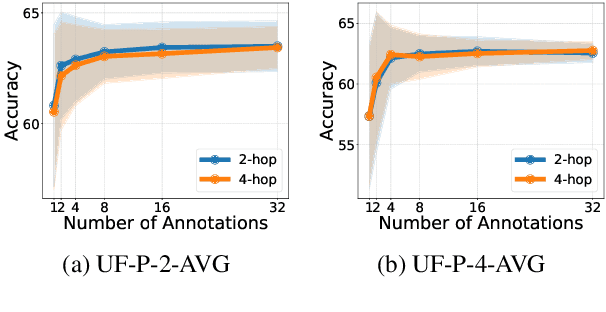
Abstract:Personalizing large language models (LLMs) is important for aligning outputs with diverse user preferences, yet existing methods struggle with flexibility and generalization. We propose CoPL (Collaborative Preference Learning), a graph-based collaborative filtering framework that models user-response relationships to enhance preference estimation, particularly in sparse annotation settings. By integrating a mixture of LoRA experts, CoPL efficiently fine-tunes LLMs while dynamically balancing shared and user-specific preferences. Additionally, an optimization-free adaptation strategy enables generalization to unseen users without fine-tuning. Experiments on UltraFeedback-P demonstrate that CoPL outperforms existing personalized reward models, effectively capturing both common and controversial preferences, making it a scalable solution for personalized LLM alignment.
GeoDANO: Geometric VLM with Domain Agnostic Vision Encoder
Feb 17, 2025Abstract:We introduce GeoDANO, a geometric vision-language model (VLM) with a domain-agnostic vision encoder, for solving plane geometry problems. Although VLMs have been employed for solving geometry problems, their ability to recognize geometric features remains insufficiently analyzed. To address this gap, we propose a benchmark that evaluates the recognition of visual geometric features, including primitives such as dots and lines, and relations such as orthogonality. Our preliminary study shows that vision encoders often used in general-purpose VLMs, e.g., OpenCLIP, fail to detect these features and struggle to generalize across domains. We develop GeoCLIP, a CLIP based model trained on synthetic geometric diagram-caption pairs to overcome the limitation. Benchmark results show that GeoCLIP outperforms existing vision encoders in recognizing geometric features. We then propose our VLM, GeoDANO, which augments GeoCLIP with a domain adaptation strategy for unseen diagram styles. GeoDANO outperforms specialized methods for plane geometry problems and GPT-4o on MathVerse.
Towards Bridging Generalization and Expressivity of Graph Neural Networks
Oct 14, 2024Abstract:Expressivity and generalization are two critical aspects of graph neural networks (GNNs). While significant progress has been made in studying the expressivity of GNNs, much less is known about their generalization capabilities, particularly when dealing with the inherent complexity of graph-structured data. In this work, we address the intricate relationship between expressivity and generalization in GNNs. Theoretical studies conjecture a trade-off between the two: highly expressive models risk overfitting, while those focused on generalization may sacrifice expressivity. However, empirical evidence often contradicts this assumption, with expressive GNNs frequently demonstrating strong generalization. We explore this contradiction by introducing a novel framework that connects GNN generalization to the variance in graph structures they can capture. This leads us to propose a $k$-variance margin-based generalization bound that characterizes the structural properties of graph embeddings in terms of their upper-bounded expressive power. Our analysis does not rely on specific GNN architectures, making it broadly applicable across GNN models. We further uncover a trade-off between intra-class concentration and inter-class separation, both of which are crucial for effective generalization. Through case studies and experiments on real-world datasets, we demonstrate that our theoretical findings align with empirical results, offering a deeper understanding of how expressivity can enhance GNN generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge