Shouheng Li
Towards Bridging Generalization and Expressivity of Graph Neural Networks
Oct 14, 2024Abstract:Expressivity and generalization are two critical aspects of graph neural networks (GNNs). While significant progress has been made in studying the expressivity of GNNs, much less is known about their generalization capabilities, particularly when dealing with the inherent complexity of graph-structured data. In this work, we address the intricate relationship between expressivity and generalization in GNNs. Theoretical studies conjecture a trade-off between the two: highly expressive models risk overfitting, while those focused on generalization may sacrifice expressivity. However, empirical evidence often contradicts this assumption, with expressive GNNs frequently demonstrating strong generalization. We explore this contradiction by introducing a novel framework that connects GNN generalization to the variance in graph structures they can capture. This leads us to propose a $k$-variance margin-based generalization bound that characterizes the structural properties of graph embeddings in terms of their upper-bounded expressive power. Our analysis does not rely on specific GNN architectures, making it broadly applicable across GNN models. We further uncover a trade-off between intra-class concentration and inter-class separation, both of which are crucial for effective generalization. Through case studies and experiments on real-world datasets, we demonstrate that our theoretical findings align with empirical results, offering a deeper understanding of how expressivity can enhance GNN generalization.
Local Vertex Colouring Graph Neural Networks
Mar 10, 2024Abstract:In recent years, there has been a significant amount of research focused on expanding the expressivity of Graph Neural Networks (GNNs) beyond the Weisfeiler-Lehman (1-WL) framework. While many of these studies have yielded advancements in expressivity, they have frequently come at the expense of decreased efficiency or have been restricted to specific types of graphs. In this study, we investigate the expressivity of GNNs from the perspective of graph search. Specifically, we propose a new vertex colouring scheme and demonstrate that classical search algorithms can efficiently compute graph representations that extend beyond the 1-WL. We show the colouring scheme inherits useful properties from graph search that can help solve problems like graph biconnectivity. Furthermore, we show that under certain conditions, the expressivity of GNNs increases hierarchically with the radius of the search neighbourhood. To further investigate the proposed scheme, we develop a new type of GNN based on two search strategies, breadth-first search and depth-first search, highlighting the graph properties they can capture on top of 1-WL. Our code is available at https://github.com/seanli3/lvc.
* 22 pages, 8 figures
Generalization of Graph Neural Networks through the Lens of Homomorphism
Mar 10, 2024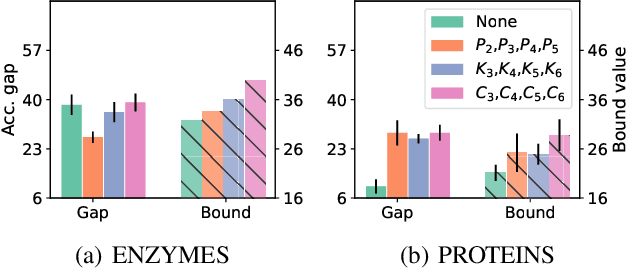
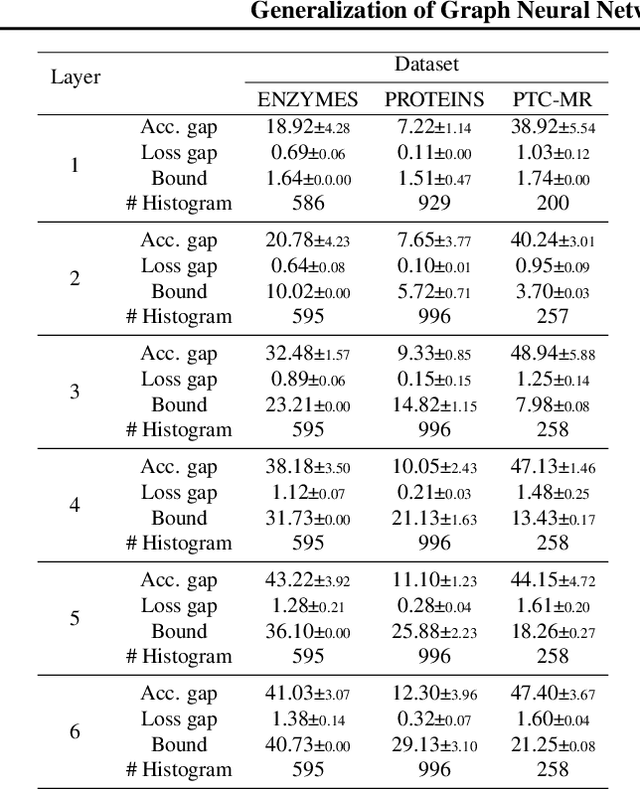
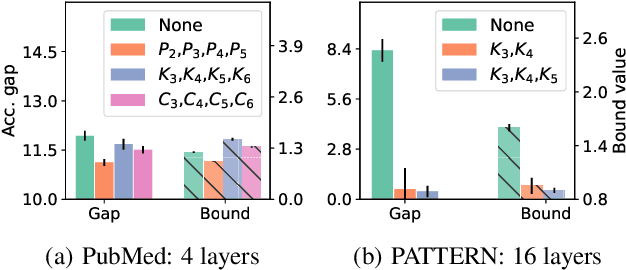
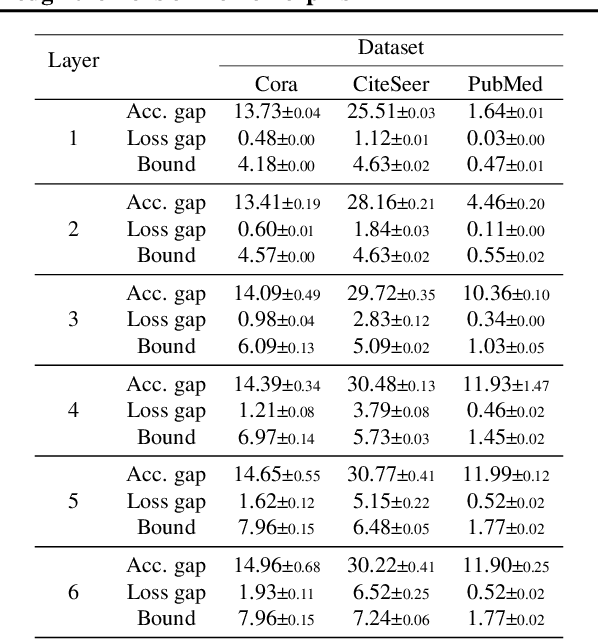
Abstract:Despite the celebrated popularity of Graph Neural Networks (GNNs) across numerous applications, the ability of GNNs to generalize remains less explored. In this work, we propose to study the generalization of GNNs through a novel perspective - analyzing the entropy of graph homomorphism. By linking graph homomorphism with information-theoretic measures, we derive generalization bounds for both graph and node classifications. These bounds are capable of capturing subtleties inherent in various graph structures, including but not limited to paths, cycles and cliques. This enables a data-dependent generalization analysis with robust theoretical guarantees. To shed light on the generality of of our proposed bounds, we present a unifying framework that can characterize a broad spectrum of GNN models through the lens of graph homomorphism. We validate the practical applicability of our theoretical findings by showing the alignment between the proposed bounds and the empirically observed generalization gaps over both real-world and synthetic datasets.
Restructuring Graph for Higher Homophily via Learnable Spectral Clustering
Jun 06, 2022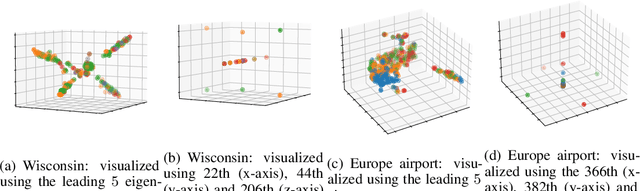
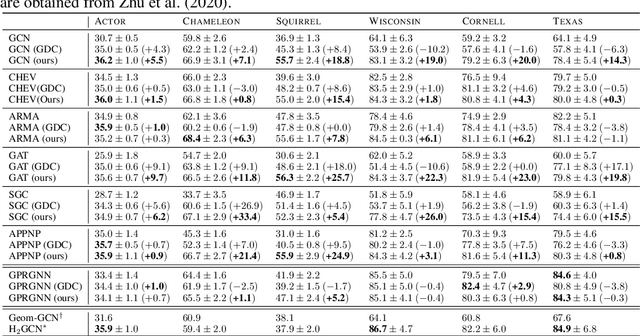
Abstract:While a growing body of literature has been studying new Graph Neural Networks (GNNs) that work on both homophilic and heterophilic graphs, little work has been done on adapting classical GNNs to less-homophilic graphs. Although lacking the ability to work with less-homophilic graphs, classical GNNs still stand out in some properties such as efficiency, simplicity and explainability. We propose a novel graph restructuring method to maximize the benefit of prevalent GNNs with the homophilic assumption. Our contribution is threefold: a) learning the weight of pseudo-eigenvectors for an adaptive spectral clustering that aligns well with known node labels, b) proposing a new homophilic metric that measures how two nodes with the same label are likely to be connected, and c) reconstructing the adjacency matrix based on the result of adaptive spectral clustering to maximize the homophilic scores. The experimental results show that our graph restructuring method can significantly boost the performance of six classical GNNs by an average of 25% on less-homophilic graphs. The boosted performance is comparable to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge