Generalization of Graph Neural Networks through the Lens of Homomorphism
Paper and Code
Mar 10, 2024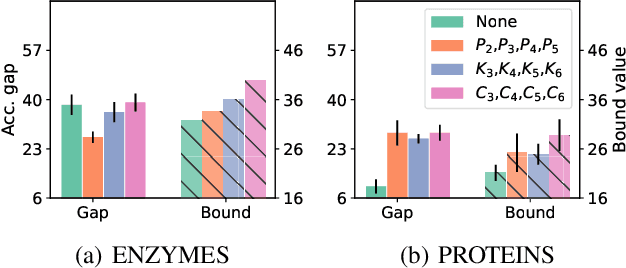
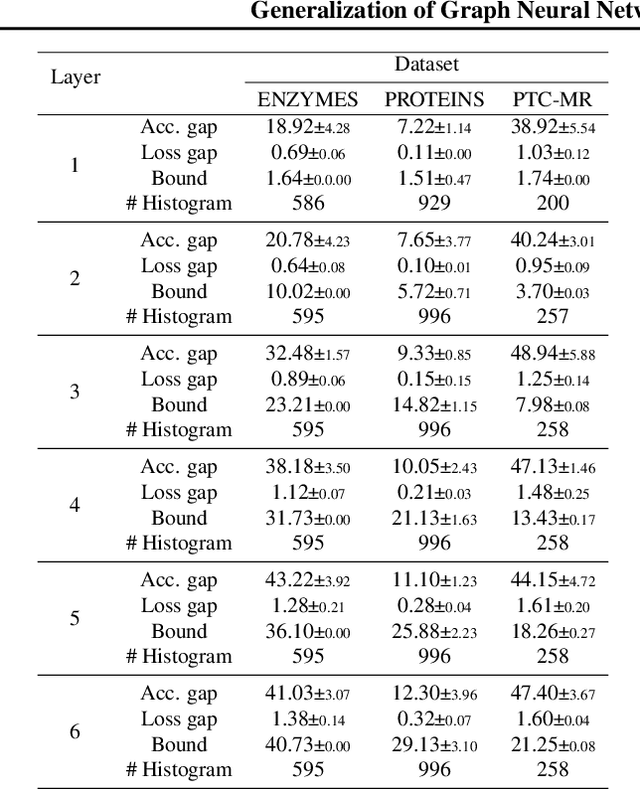
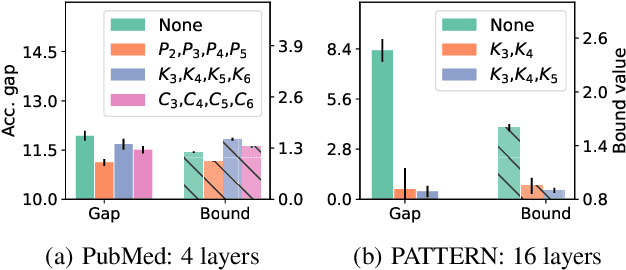
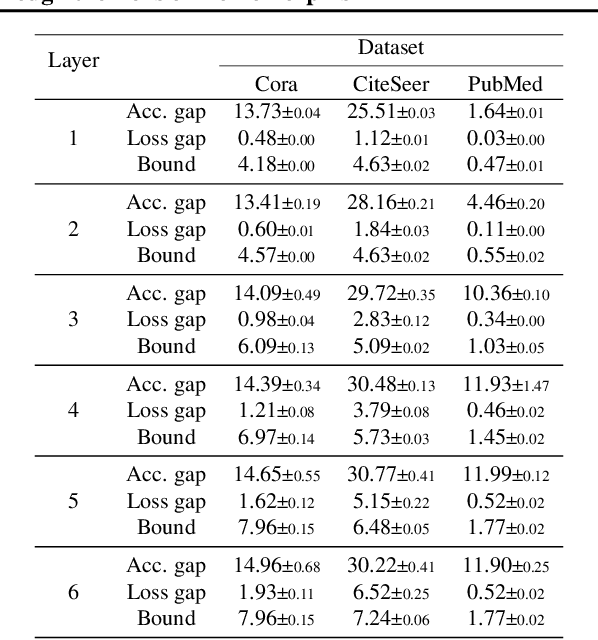
Despite the celebrated popularity of Graph Neural Networks (GNNs) across numerous applications, the ability of GNNs to generalize remains less explored. In this work, we propose to study the generalization of GNNs through a novel perspective - analyzing the entropy of graph homomorphism. By linking graph homomorphism with information-theoretic measures, we derive generalization bounds for both graph and node classifications. These bounds are capable of capturing subtleties inherent in various graph structures, including but not limited to paths, cycles and cliques. This enables a data-dependent generalization analysis with robust theoretical guarantees. To shed light on the generality of of our proposed bounds, we present a unifying framework that can characterize a broad spectrum of GNN models through the lens of graph homomorphism. We validate the practical applicability of our theoretical findings by showing the alignment between the proposed bounds and the empirically observed generalization gaps over both real-world and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge