Restructuring Graph for Higher Homophily via Learnable Spectral Clustering

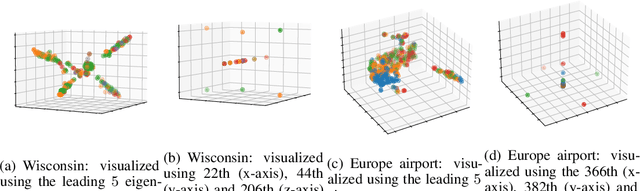
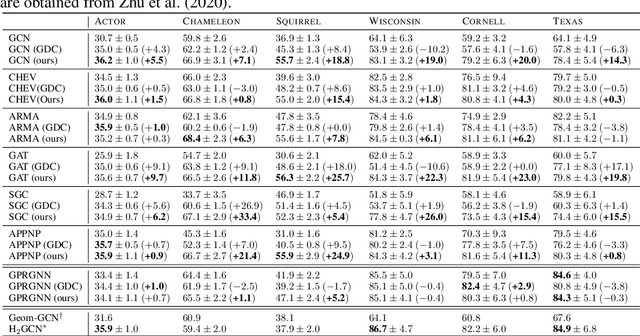
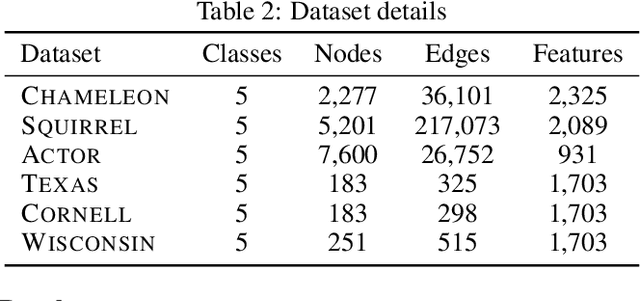
While a growing body of literature has been studying new Graph Neural Networks (GNNs) that work on both homophilic and heterophilic graphs, little work has been done on adapting classical GNNs to less-homophilic graphs. Although lacking the ability to work with less-homophilic graphs, classical GNNs still stand out in some properties such as efficiency, simplicity and explainability. We propose a novel graph restructuring method to maximize the benefit of prevalent GNNs with the homophilic assumption. Our contribution is threefold: a) learning the weight of pseudo-eigenvectors for an adaptive spectral clustering that aligns well with known node labels, b) proposing a new homophilic metric that measures how two nodes with the same label are likely to be connected, and c) reconstructing the adjacency matrix based on the result of adaptive spectral clustering to maximize the homophilic scores. The experimental results show that our graph restructuring method can significantly boost the performance of six classical GNNs by an average of 25% on less-homophilic graphs. The boosted performance is comparable to state-of-the-art methods.