Long Live the Librarian! A Persistent Search Sub-Agent for Energy-Efficient Multi-Agent Software Engineering Systems

Multi-agent systems (MAS) have substantially advanced autonomous software engineering (SWE), but their growing inference energy demands raise sustainability concerns. In this paper, we demonstrate that this cost is concentrated in an overlooked source: redundant output tokens generated across agents. Two empirical findings ground this claim. First, our per-token energy attribution for MAS reveals a sharp asymmetry: an output token consumes 30 to 1,000 times more energy than an input or cached token. Second, MAS inflate per-episode output because agents repeatedly re-explore overlapping repository regions. To address this inefficiency, we propose Librarian, a persistent search sub-agent that tracks repository-search history and suppresses redundant exploration actions across agents. By returning short references to file regions instead of full file excerpts, Librarian further reduces output-token volume. On SWE-Bench Verified, Librarian reduces per-episode GPU energy consumption of existing multi-agent SWE systems by up to 25% while preserving task performance.

Transductive Generalization via Optimal Transport and Its Application to Graph Node Classification

Many existing transductive bounds rely on classical complexity measures that are computationally intractable and often misaligned with empirical behavior. In this work, we establish new representation-based generalization bounds in a distribution-free transductive setting, where learned representations are dependent, and test features are accessible during training. We derive global and class-wise bounds via optimal transport, expressed in terms of Wasserstein distances between encoded feature distributions. We demonstrate that our bounds are efficiently computable and strongly correlate with empirical generalization in graph node classification, improving upon classical complexity measures. Additionally, our analysis reveals how the GNN aggregation process transforms the representation distributions, inducing a trade-off between intra-class concentration and inter-class separation. This yields depth-dependent characterizations that capture the non-monotonic relationship between depth and generalization error observed in practice. The code is available at https://github.com/ml-postech/Transductive-OT-Gen-Bound.

Training-free Composition of Pre-trained GFlowNets for Multi-Objective Generation

Generative Flow Networks (GFlowNets) learn to sample diverse candidates in proportion to a reward function, making them well-suited for scientific discovery, where exploring multiple promising solutions is crucial. Further extending GFlowNets to multi-objective settings has attracted growing interest since real-world applications often involve multiple, conflicting objectives. However, existing approaches require additional training for each set of objectives, limiting their applicability and incurring substantial computational overhead. We propose a training-free mixing policy that composes pre-trained GFlowNets at inference time, enabling rapid adaptation without finetuning or retraining. Importantly, our framework is flexible, capable of handling diverse reward combinations ranging from linear scalarization to complex non-linear logical operators, which are often handled separately in previous literature. We prove that our method exactly recovers the target distribution for linear scalarization and quantify the approximation quality for nonlinear operators through a distortion factor. Experiments on a synthetic 2D grid and real-world molecule-generation tasks demonstrate that our approach achieves performance comparable to baselines that require additional training.

In-Place Feedback: A New Paradigm for Guiding LLMs in Multi-Turn Reasoning

Large language models (LLMs) are increasingly studied in the context of multi-turn reasoning, where models iteratively refine their outputs based on user-provided feedback. Such settings are crucial for tasks that require complex reasoning, yet existing feedback paradigms often rely on issuing new messages. LLMs struggle to integrate these reliably, leading to inconsistent improvements. In this work, we introduce in-place feedback, a novel interaction paradigm in which users directly edit an LLM's previous response, and the model conditions on this modified response to generate its revision. Empirical evaluations on diverse reasoning-intensive benchmarks reveal that in-place feedback achieves better performance than conventional multi-turn feedback while using $79.1\%$ fewer tokens. Complementary analyses on controlled environments further demonstrate that in-place feedback resolves a core limitation of multi-turn feedback: models often fail to apply feedback precisely to erroneous parts of the response, leaving errors uncorrected and sometimes introducing new mistakes into previously correct content. These findings suggest that in-place feedback offers a more natural and effective mechanism for guiding LLMs in reasoning-intensive tasks.

Influence Functions for Edge Edits in Non-Convex Graph Neural Networks

Understanding how individual edges influence the behavior of graph neural networks (GNNs) is essential for improving their interpretability and robustness. Graph influence functions have emerged as promising tools to efficiently estimate the effects of edge deletions without retraining. However, existing influence prediction methods rely on strict convexity assumptions, exclusively consider the influence of edge deletions while disregarding edge insertions, and fail to capture changes in message propagation caused by these modifications. In this work, we propose a proximal Bregman response function specifically tailored for GNNs, relaxing the convexity requirement and enabling accurate influence prediction for standard neural network architectures. Furthermore, our method explicitly accounts for message propagation effects and extends influence prediction to both edge deletions and insertions in a principled way. Experiments with real-world datasets demonstrate accurate influence predictions for different characteristics of GNNs. We further demonstrate that the influence function is versatile in applications such as graph rewiring and adversarial attacks.

The Oversmoothing Fallacy: A Misguided Narrative in GNN Research

Oversmoothing has been recognized as a main obstacle to building deep Graph Neural Networks (GNNs), limiting the performance. This position paper argues that the influence of oversmoothing has been overstated and advocates for a further exploration of deep GNN architectures. Given the three core operations of GNNs, aggregation, linear transformation, and non-linear activation, we show that prior studies have mistakenly confused oversmoothing with the vanishing gradient, caused by transformation and activation rather than aggregation. Our finding challenges prior beliefs about oversmoothing being unique to GNNs. Furthermore, we demonstrate that classical solutions such as skip connections and normalization enable the successful stacking of deep GNN layers without performance degradation. Our results clarify misconceptions about oversmoothing and shed new light on the potential of deep GNNs.

CoPL: Collaborative Preference Learning for Personalizing LLMs

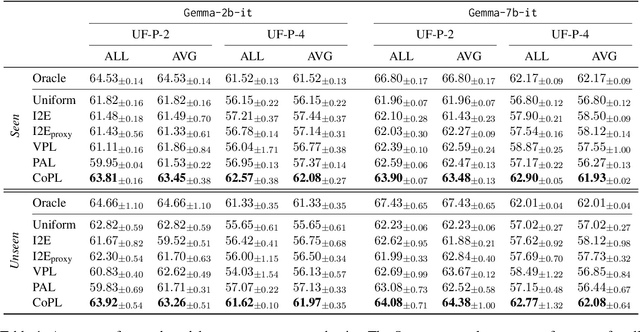
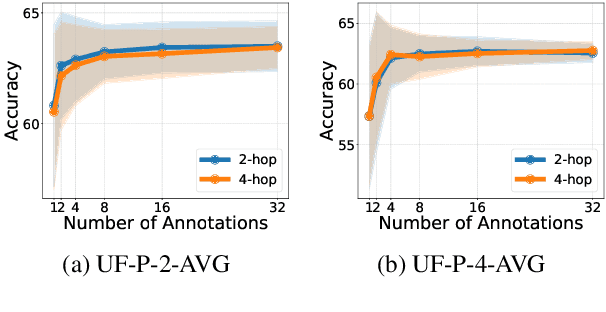
Personalizing large language models (LLMs) is important for aligning outputs with diverse user preferences, yet existing methods struggle with flexibility and generalization. We propose CoPL (Collaborative Preference Learning), a graph-based collaborative filtering framework that models user-response relationships to enhance preference estimation, particularly in sparse annotation settings. By integrating a mixture of LoRA experts, CoPL efficiently fine-tunes LLMs while dynamically balancing shared and user-specific preferences. Additionally, an optimization-free adaptation strategy enables generalization to unseen users without fine-tuning. Experiments on UltraFeedback-P demonstrate that CoPL outperforms existing personalized reward models, effectively capturing both common and controversial preferences, making it a scalable solution for personalized LLM alignment.

Taming Gradient Oversmoothing and Expansion in Graph Neural Networks

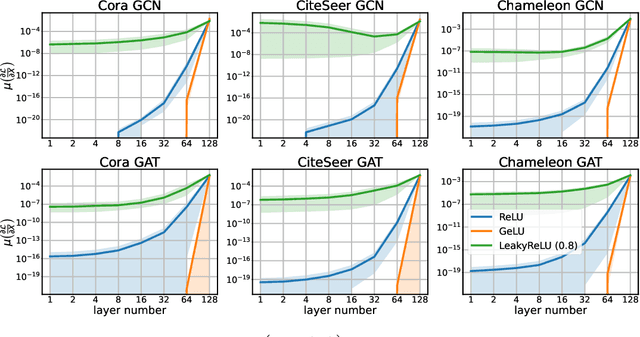
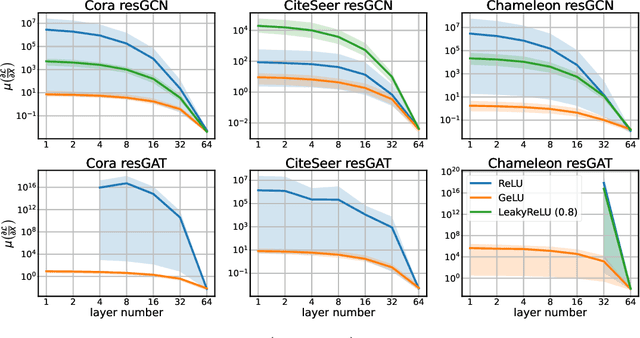
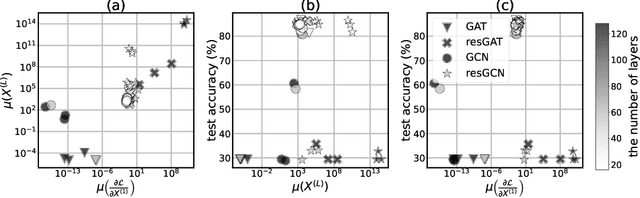
Oversmoothing has been claimed as a primary bottleneck for multi-layered graph neural networks (GNNs). Multiple analyses have examined how and why oversmoothing occurs. However, none of the prior work addressed how optimization is performed under the oversmoothing regime. In this work, we show the presence of $\textit{gradient oversmoothing}$ preventing optimization during training. We further analyze that GNNs with residual connections, a well-known solution to help gradient flow in deep architecture, introduce $\textit{gradient expansion}$, a phenomenon of the gradient explosion in diverse directions. Therefore, adding residual connections cannot be a solution for making a GNN deep. Our analysis reveals that constraining the Lipschitz bound of each layer can neutralize the gradient expansion. To this end, we provide a simple yet effective normalization method to prevent the gradient expansion. An empirical study shows that the residual GNNs with hundreds of layers can be efficiently trained with the proposed normalization without compromising performance. Additional studies show that the empirical observations corroborate our theoretical analysis.

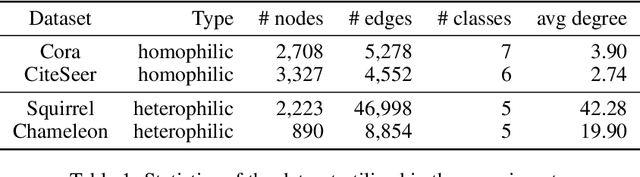
Distinguishing Neighborhood Representations Through Reverse Process of GNNs for Heterophilic Graphs

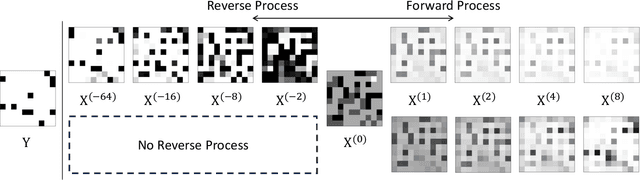
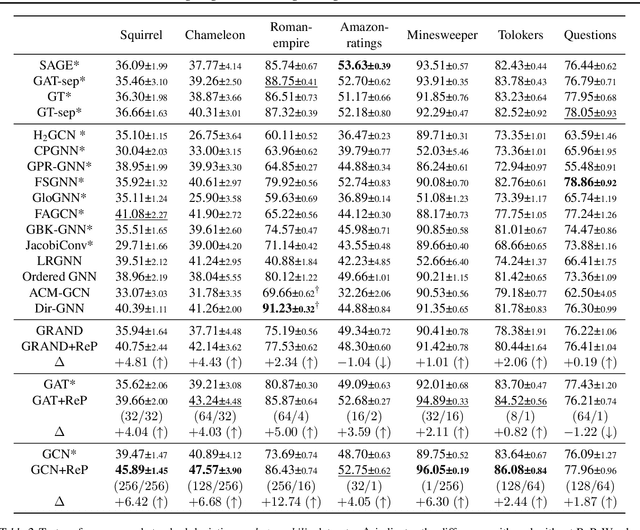
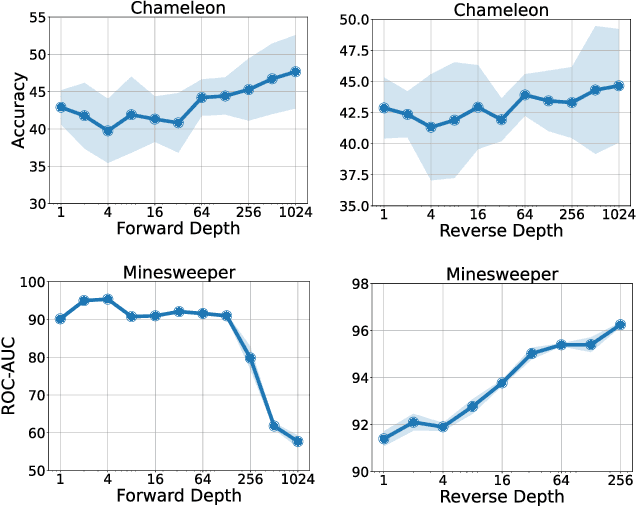
Graph Neural Network (GNN) resembles the diffusion process, leading to the over-smoothing of learned representations when stacking many layers. Hence, the reverse process of message passing can sharpen the node representations by inverting the forward message propagation. The sharpened representations can help us to better distinguish neighboring nodes with different labels, such as in heterophilic graphs. In this work, we apply the design principle of the reverse process to the three variants of the GNNs. Through the experiments on heterophilic graph data, where adjacent nodes need to have different representations for successful classification, we show that the reverse process significantly improves the prediction performance in many cases. Additional analysis reveals that the reverse mechanism can mitigate the over-smoothing over hundreds of layers.

SpReME: Sparse Regression for Multi-Environment Dynamic Systems

Learning dynamical systems is a promising avenue for scientific discoveries. However, capturing the governing dynamics in multiple environments still remains a challenge: model-based approaches rely on the fidelity of assumptions made for a single environment, whereas data-driven approaches based on neural networks are often fragile on extrapolating into the future. In this work, we develop a method of sparse regression dubbed SpReME to discover the major dynamics that underlie multiple environments. Specifically, SpReME shares a sparse structure of ordinary differential equation (ODE) across different environments in common while allowing each environment to keep the coefficients of ODE terms independently. We demonstrate that the proposed model captures the correct dynamics from multiple environments over four different dynamic systems with improved prediction performance.