MeshDMP: Motion Planning on Discrete Manifolds using Dynamic Movement Primitives

An open problem in industrial automation is to reliably perform tasks requiring in-contact movements with complex workpieces, as current solutions lack the ability to seamlessly adapt to the workpiece geometry. In this paper, we propose a Learning from Demonstration approach that allows a robot manipulator to learn and generalise motions across complex surfaces by leveraging differential mathematical operators on discrete manifolds to embed information on the geometry of the workpiece extracted from triangular meshes, and extend the Dynamic Movement Primitives (DMPs) framework to generate motions on the mesh surfaces. We also propose an effective strategy to adapt the motion to different surfaces, by introducing an isometric transformation of the learned forcing term. The resulting approach, namely MeshDMP, is evaluated both in simulation and real experiments, showing promising results in typical industrial automation tasks like car surface polishing.

Interactive Learning of Physical Object Properties Through Robot Manipulation and Database of Object Measurements

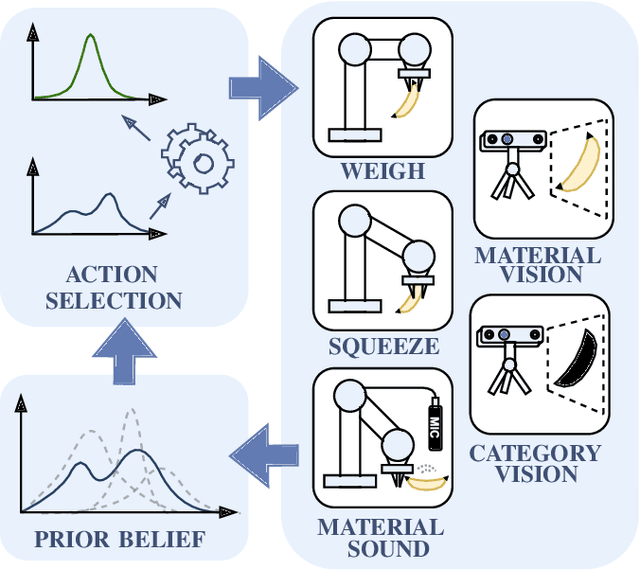
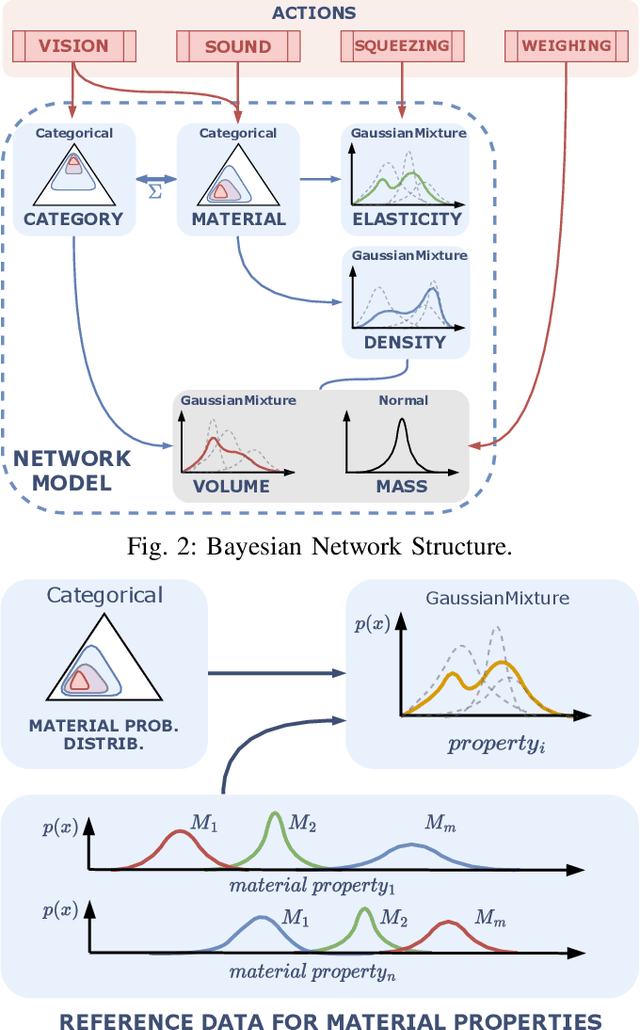
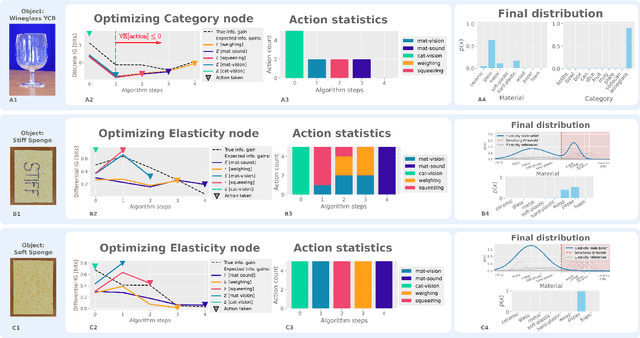
This work presents a framework for automatically extracting physical object properties, such as material composition, mass, volume, and stiffness, through robot manipulation and a database of object measurements. The framework involves exploratory action selection to maximize learning about objects on a table. A Bayesian network models conditional dependencies between object properties, incorporating prior probability distributions and uncertainty associated with measurement actions. The algorithm selects optimal exploratory actions based on expected information gain and updates object properties through Bayesian inference. Experimental evaluation demonstrates effective action selection compared to a baseline and correct termination of the experiments if there is nothing more to be learned. The algorithm proved to behave intelligently when presented with trick objects with material properties in conflict with their appearance. The robot pipeline integrates with a logging module and an online database of objects, containing over 24,000 measurements of 63 objects with different grippers. All code and data are publicly available, facilitating automatic digitization of objects and their physical properties through exploratory manipulations.

Fusion Dynamical Systems with Machine Learning in Imitation Learning: A Comprehensive Overview

Imitation Learning (IL), also referred to as Learning from Demonstration (LfD), holds significant promise for capturing expert motor skills through efficient imitation, facilitating adept navigation of complex scenarios. A persistent challenge in IL lies in extending generalization from historical demonstrations, enabling the acquisition of new skills without re-teaching. Dynamical system-based IL (DSIL) emerges as a significant subset of IL methodologies, offering the ability to learn trajectories via movement primitives and policy learning based on experiential abstraction. This paper emphasizes the fusion of theoretical paradigms, integrating control theory principles inherent in dynamical systems into IL. This integration notably enhances robustness, adaptability, and convergence in the face of novel scenarios. This survey aims to present a comprehensive overview of DSIL methods, spanning from classical approaches to recent advanced approaches. We categorize DSIL into autonomous dynamical systems and non-autonomous dynamical systems, surveying traditional IL methods with low-dimensional input and advanced deep IL methods with high-dimensional input. Additionally, we present and analyze three main stability methods for IL: Lyapunov stability, contraction theory, and diffeomorphism mapping. Our exploration also extends to popular policy improvement methods for DSIL, encompassing reinforcement learning, deep reinforcement learning, and evolutionary strategies.

Safe Execution of Learned Orientation Skills with Conic Control Barrier Functions

In the field of Learning from Demonstration (LfD), Dynamical Systems (DSs) have gained significant attention due to their ability to generate real-time motions and reach predefined targets. However, the conventional convergence-centric behavior exhibited by DSs may fall short in safety-critical tasks, specifically, those requiring precise replication of demonstrated trajectories or strict adherence to constrained regions even in the presence of perturbations or human intervention. Moreover, existing DS research often assumes demonstrations solely in Euclidean space, overlooking the crucial aspect of orientation in various applications. To alleviate these shortcomings, we present an innovative approach geared toward ensuring the safe execution of learned orientation skills within constrained regions surrounding a reference trajectory. This involves learning a stable DS on SO(3), extracting time-varying conic constraints from the variability observed in expert demonstrations, and bounding the evolution of the DS with Conic Control Barrier Function (CCBF) to fulfill the constraints. We validated our approach through extensive evaluation in simulation and showcased its effectiveness for a cutting skill in the context of assisted teleoperation.

Orientation Control with Variable Stiffness Dynamical Systems

Recently, several approaches have attempted to combine motion generation and control in one loop to equip robots with reactive behaviors, that cannot be achieved with traditional time-indexed tracking controllers. These approaches however mainly focused on positions, neglecting the orientation part which can be crucial to many tasks e.g. screwing. In this work, we propose a control algorithm that adapts the robot's rotational motion and impedance in a closed-loop manner. Given a first-order Dynamical System representing an orientation motion plan and a desired rotational stiffness profile, our approach enables the robot to follow the reference motion with an interactive behavior specified by the desired stiffness, while always being aware of the current orientation, represented as a Unit Quaternion (UQ). We rely on the Lie algebra to formulate our algorithm, since unlike positions, UQ feature constraints that should be respected in the devised controller. We validate our proposed approach in multiple robot experiments, showcasing the ability of our controller to follow complex orientation profiles, react safely to perturbations, and fulfill physical interaction tasks.

SPONGE: Sequence Planning with Deformable-ON-Rigid Contact Prediction from Geometric Features

Planning robotic manipulation tasks, especially those that involve interaction between deformable and rigid objects, is challenging due to the complexity in predicting such interactions. We introduce SPONGE, a sequence planning pipeline powered by a deep learning-based contact prediction model for contacts between deformable and rigid bodies under interactions. The contact prediction model is trained on synthetic data generated by a developed simulation environment to learn the mapping from point-cloud observation of a rigid target object and the pose of a deformable tool, to 3D representation of the contact points between the two bodies. We experimentally evaluated the proposed approach for a dish cleaning task both in simulation and on a real \panda with real-world objects. The experimental results demonstrate that in both scenarios the proposed planning pipeline is capable of generating high-quality trajectories that can accomplish the task by achieving more than 90\% area coverage on different objects of varying sizes and curvatures while minimizing travel distance. Code and video are available at: \url{https://irobotics.aalto.fi/sponge/}.

QDP: Learning to Sequentially Optimise Quasi-Static and Dynamic Manipulation Primitives for Robotic Cloth Manipulation

Pre-defined manipulation primitives are widely used for cloth manipulation. However, cloth properties such as its stiffness or density can highly impact the performance of these primitives. Although existing solutions have tackled the parameterisation of pick and place locations, the effect of factors such as the velocity or trajectory of quasi-static and dynamic manipulation primitives has been neglected. Choosing appropriate values for these parameters is crucial to cope with the range of materials present in house-hold cloth objects. To address this challenge, we introduce the Quasi-Dynamic Parameterisable (QDP) method, which optimises parameters such as the motion velocity in addition to the pick and place positions of quasi-static and dynamic manipulation primitives. In this work, we leverage the framework of Sequential Reinforcement Learning to decouple sequentially the parameters that compose the primitives. To evaluate the effectiveness of the method we focus on the task of cloth unfolding with a robotic arm in simulation and real-world experiments. Our results in simulation show that by deciding the optimal parameters for the primitives the performance can improve by 20% compared to sub-optimal ones. Real-world results demonstrate the advantage of modifying the velocity and height of manipulation primitives for cloths with different mass, stiffness, shape and size. Supplementary material, videos, and code, can be found at https://sites.google.com/view/qdp-srl.

Trajectory Optimization on Matrix Lie Groups with Differential Dynamic Programming and Nonlinear Constraints

Matrix Lie groups are an important class of manifolds commonly used in control and robotics, and the optimization of control policies on these manifolds is a fundamental problem. In this work, we propose a novel approach for trajectory optimization on matrix Lie groups using an augmented Lagrangian based constrained discrete Differential Dynamic Programming (DDP) algorithm. Our method involves lifting the optimization problem to the Lie algebra in the backward pass and retracting back to the manifold in the forward pass. In contrast to previous approaches which only addressed constraint handling for specific classes of matrix Lie groups, our method provides a general approach for nonlinear constraint handling for a generic matrix Lie groups. We also demonstrate the effectiveness of our method in handling external disturbances through its application as a Lie-algebraic feedback control policy on SE(3). The results show that our approach is able to effectively handle configuration, velocity and input constraints and maintain stability in the presence of external disturbances.

Learning Deep Robotic Skills on Riemannian manifolds

In this paper, we propose RiemannianFlow, a deep generative model that allows robots to learn complex and stable skills evolving on Riemannian manifolds. Examples of Riemannian data in robotics include stiffness (symmetric and positive definite matrix (SPD)) and orientation (unit quaternion (UQ)) trajectories. For Riemannian data, unlike Euclidean ones, different dimensions are interconnected by geometric constraints which have to be properly considered during the learning process. Using distance preserving mappings, our approach transfers the data between their original manifold and the tangent space, realizing the removing and re-fulfilling of the geometric constraints. This allows to extend existing frameworks to learn stable skills from Riemannian data while guaranteeing the stability of the learning results. The ability of RiemannianFlow to learn various data patterns and the stability of the learned models are experimentally shown on a dataset of manifold motions. Further, we analyze from different perspectives the robustness of the model with different hyperparameter combinations. It turns out that the model's stability is not affected by different hyperparameters, a proper combination of the hyperparameters leads to a significant improvement (up to 27.6%) of the model accuracy. Last, we show the effectiveness of RiemannianFlow in a real peg-in-hole (PiH) task where we need to generate stable and consistent position and orientation trajectories for the robot starting from different initial poses.

Geometric Reinforcement Learning: The Case of Cartesian Space Orientation

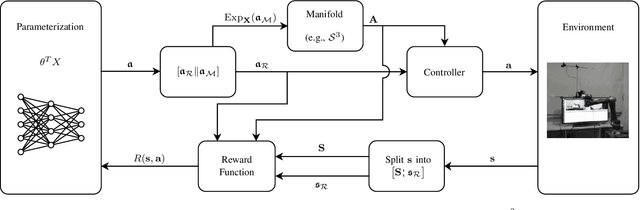
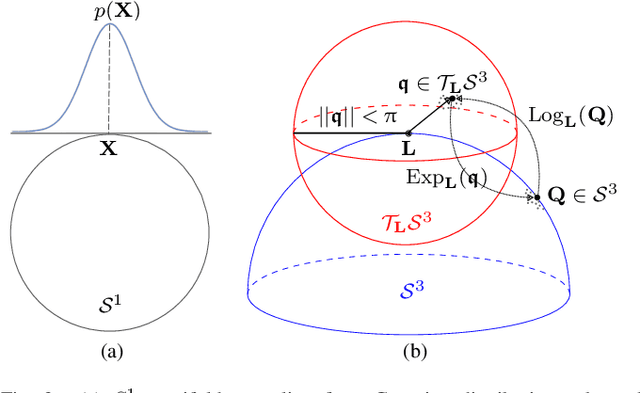
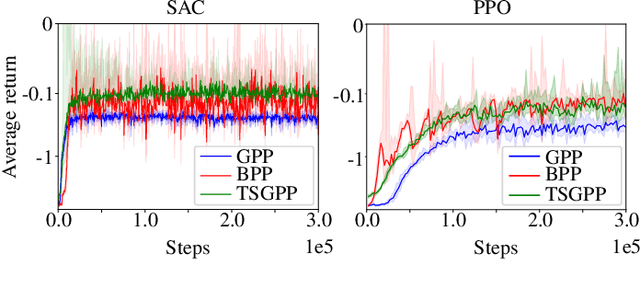
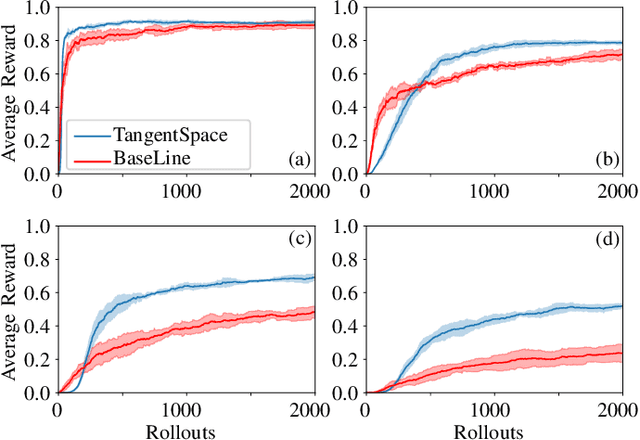
Reinforcement learning (RL) enables an agent to learn by trial and error while interacting with a dynamic environment. Traditionally, RL is used to learn and predict Euclidean robotic manipulation skills like positions, velocities, and forces. However, in robotics, it is common to have non-Euclidean data like orientation or stiffness, and neglecting their geometric nature can adversely affect learning performance and accuracy. In this paper, we propose a novel framework for RL by using Riemannian geometry, and show how it can be applied to learn manipulation skills with a specific geometric structure (e.g., robot's orientation in the task space). The proposed framework is suitable for any policy representation and is independent of the algorithm choice. Specifically, we propose to apply policy parameterization and learning on the tangent space, then map the learned actions back to the appropriate manifold (e.g., the S3 manifold for orientation). Therefore, we introduce a geometrically grounded pre- and post-processing step into the typical RL pipeline, which opens the door to all algorithms designed for Euclidean space to learn from non-Euclidean data without changes. Experimental results, obtained both in simulation and on a real robot, support our hypothesis that learning on the tangent space is more accurate and converges to a better solution than approximating non-Euclidean data.