Social Robot Navigation with Adaptive Proxemics Based on Emotions

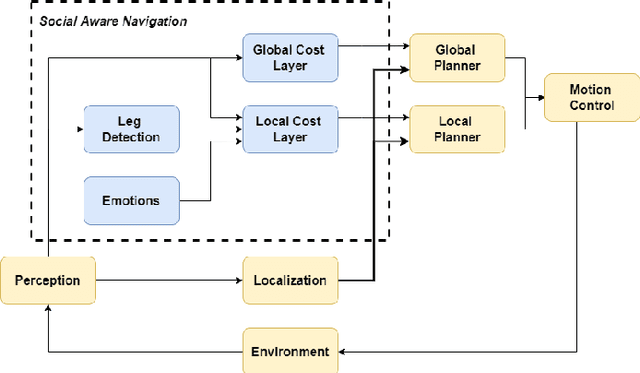
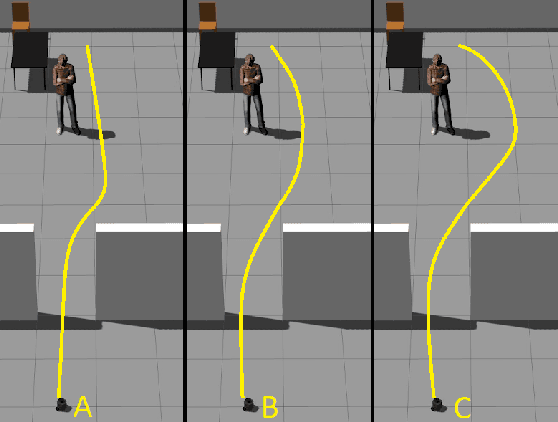
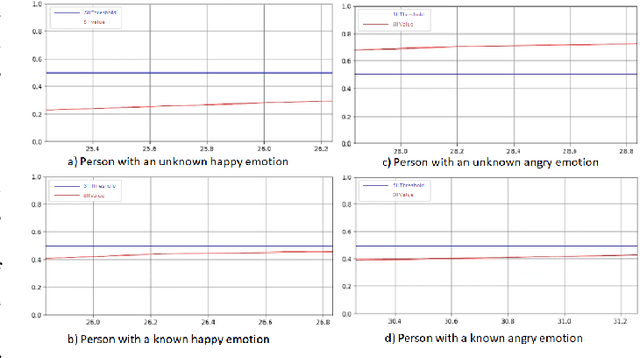
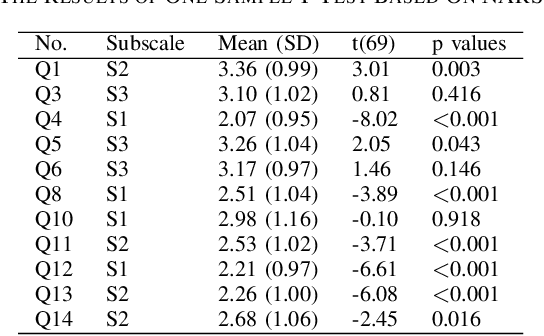
The primary aim of this paper is to investigate the integration of emotions into the social navigation framework to analyse its effect on both navigation and human physiological safety and comfort. The proposed framework uses leg detection to find the whereabouts of people and computes adaptive proxemic zones based on their emotional state. We designed several case studies in a simulated environment and examined 3 different emotions; positive (happy), neutral and negative (angry). A survey study was conducted with 70 participants to explore their impressions about the navigation of the robot and compare the human safety and comfort measurements results. Both survey and simulation results showed that integrating emotions into proxemic zones has a significant effect on the physical safety of a human. The results revealed that when a person is angry, the robot is expected to navigate further than the standard distance to support his/her physiological comfort and safety. The results also showed that reducing the navigation distance is not preferred when a person is happy.

Geometric Reinforcement Learning: The Case of Cartesian Space Orientation

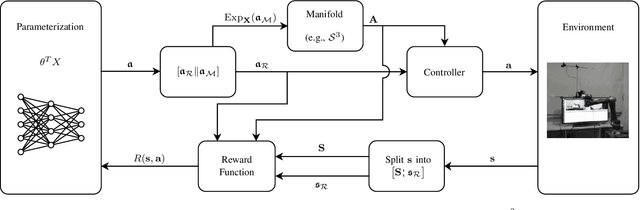
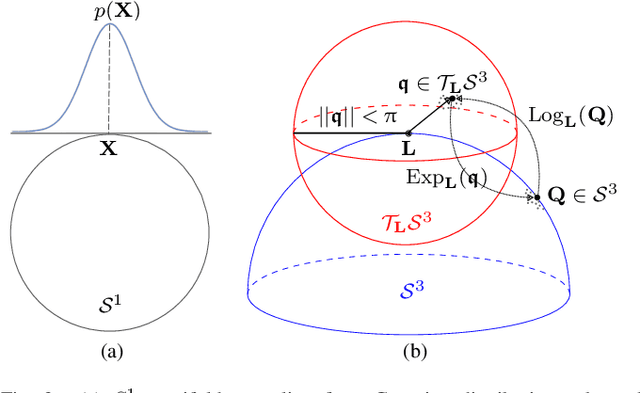
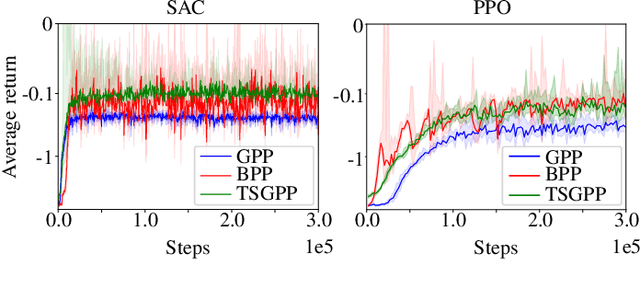
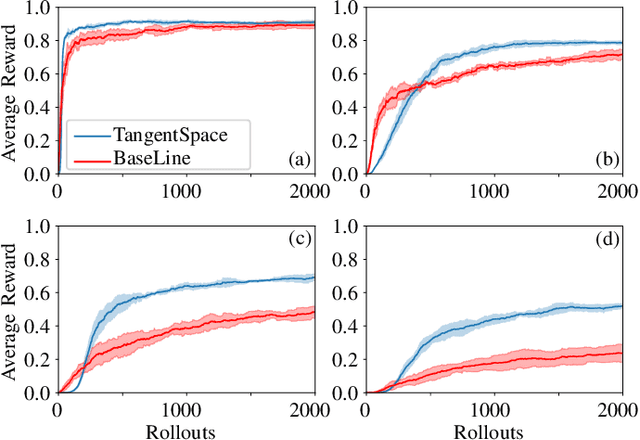
Reinforcement learning (RL) enables an agent to learn by trial and error while interacting with a dynamic environment. Traditionally, RL is used to learn and predict Euclidean robotic manipulation skills like positions, velocities, and forces. However, in robotics, it is common to have non-Euclidean data like orientation or stiffness, and neglecting their geometric nature can adversely affect learning performance and accuracy. In this paper, we propose a novel framework for RL by using Riemannian geometry, and show how it can be applied to learn manipulation skills with a specific geometric structure (e.g., robot's orientation in the task space). The proposed framework is suitable for any policy representation and is independent of the algorithm choice. Specifically, we propose to apply policy parameterization and learning on the tangent space, then map the learned actions back to the appropriate manifold (e.g., the S3 manifold for orientation). Therefore, we introduce a geometrically grounded pre- and post-processing step into the typical RL pipeline, which opens the door to all algorithms designed for Euclidean space to learn from non-Euclidean data without changes. Experimental results, obtained both in simulation and on a real robot, support our hypothesis that learning on the tangent space is more accurate and converges to a better solution than approximating non-Euclidean data.